Up: Publication homepage
A Synchronizable Transactional Database
Alexy Khrabrov, Sumeet Sobti, and Peter Yianilos1
December 4, 1999
Abstract:
A database system that can efficiently
synchronize all
or a part of its contents over a limited bandwidth link is
described.
The lowest layer of the system implements a transactional
block store of novel design. On top of this is a new enhanced
form of B+-tree that can efficiently compute a digest(hash) of
the records within any range of key values in 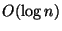 time. The top level is a communication protocol that directs
the synchronization process so that minimization of bits
communicated, rounds of communication, and local computation
are simultaneously addressed.
time. The top level is a communication protocol that directs
the synchronization process so that minimization of bits
communicated, rounds of communication, and local computation
are simultaneously addressed.
The entire synchronizable database is experimentally measured,
and the results confirm our analysis. Experiments and
comparisons are also reported for the system's two lower layers
performing conventional database operations.
Finally we suggest that our notion of a synchronizable
transactional database, as well as our implementation, might
serve as a building block for applications ranging from
digital libraries to distributed file systems and electronic
commerce.
We describe the design and implementation of an experimental
database system that includes among its basic functions the
ability to efficiently synchronize all data within a
specified key range, over a limited bandwidth link.
This simple abstraction of efficient pairwise range synchronization
may be viewed as a new building block for the construction
of advanced distributed systems, and was motivated in part
by our own work on the intermemory project [CEG+99,GY98].
Our architecture and implementation of a synchronizable transactional
database consists of three layers. The bottom bedrock layer implements
a novel block-oriented storage abstraction with transactional support
[GR92]. On top of it we build an enhanced B+-tree that supports an
additional operation to efficiently compute a digest(hash) of the records within
specified range of key values. This is our bxtree layer. The top layer
osynch implements a communication protocol for pairwise range
synchronization that uses the digest function of bxtree to simultaneously reduce
local computation, bits communicated, as well as communication rounds.
The bedrock abstraction consists of an array of fixed length blocks
addressed by logical index. In addition to allocate, free, read, and
write operations, the abstraction provides a function to atomically
commit all changes to the array. During operation a block
mapping system redirects writes intended to overwrite a given logical
block address, instead to a free physical block -- leaving the original data
intact. At the same time this logical address is tentatively mapped
to the physical block containing the new data written. The commit
operation atomically switches all maps in memory and on disk so that
these tentative mappings are made permanent. In this way bedrock
provides transactional support at the lowest level of the system.
Higher level applications, including our synchronizable database
system, may then use bedrock to build arbitrary data structures that
inherit from below a transactional capability.
Bedrock operates within a single preallocated file2 and uses no outside logging
facility. Following a system crash (see [GP94,NFSa,NFSb] for
more about failure models), no recovery process is required. The
data-store is instantly available in its most recently committed state.
Bedrock uses a three-level mapping system that supports up to 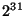 fixed length blocks. As such we suggest that it represents an
easy-to-administer and scalable substrate for many applications that
require simple transactional support.
fixed length blocks. As such we suggest that it represents an
easy-to-administer and scalable substrate for many applications that
require simple transactional support.
The bxtree layer of our system implements a B+-tree on top of bedrock.
It features support for variable length records and keys, and all data
are written in a portable (byte order independent) fashion.
Maintained along with each data record is a fixed-length digest
computed by a cryptographically strong function such as the well known
MD5 algorithm. bxtree extends a conventional B+-tree by providing a
function that given a range of key values, efficiently computes the
exclusive or (XOR) of the digest values associated with each record in the
specified range. It does this by maintaining at each internal tree
node, the XOR of all children. With this approach this MD5/XOR summary of an
arbitrary range in the database may be computed in 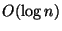 time where
time where
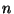 denotes the number of records in the database.
denotes the number of records in the database.
With our osynch protocol, the two parties exchange digests of key ranges
and subranges to rapidly identify regions of discrepancy. These
discrepancies are then dealt with by exchanging data.
Our design of osynch (and bxtree below) is aimed at minimizing
the complexity of synchronization measured in terms of
bits communicated, rounds of communication, and local computation.
The protocol has a simple recursive structure and may be modified
to adjust the tradeoff between these three objectives.
As implemented it reflects a tradeoff that seems appropriate for
today's computational and internet environment. See [TM96]
for related work that addresses the synchronization problem for
unstructured text/binary files.
The number of rounds is asymptotically 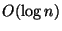 to identify each
region of discrepancy, and the local computation is
to identify each
region of discrepancy, and the local computation is
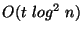 where
where 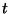 denotes the total number of discrepancies. The end result
is that the total bits communicated is roughly proportional in theory
and practice to the amount of differing data.
denotes the total number of discrepancies. The end result
is that the total bits communicated is roughly proportional in theory
and practice to the amount of differing data.
Section 2 of this paper describes the bedrock layer,
while bxtree and osynch are presented in section 3.
These sections provide additional motivation and describe our design
and implementation.
Section 4 describes our experimental studies of
all three levels. The overall synchronization system is measured with
respect to communication rounds and total data transmitted. The
results confirm our analysis. The bedrock layer's throughput is
measured and compared with that of a modern database system
[SO92,BDB] operating in simple block mode. The result is that
bedrock is somewhat more efficient in performing its task. The
combined bxtree/osynch layers are compared against the same system.
The comparison is in terms of conventional database operations, not
synchronization. Our experimental implementation is competitive only
in the large database regime, and even there is somewhat slower. We
attribute this to the fact that an in-memory B-tree block management
system is not yet part of our implementation, and expect that the
addition of this facility will narrow or eliminate the gap.
Bedrock Transactional Memory
Large databases and other complex data structures maintained in non-volatile
storage, e.g. on disk, often have certain important invariants to be preserved
at all times for the data to make sense. In order to write data with the
invariants always preserved, the updates must be made transactionally
[GR92]. It is desirable to have an abstraction of transactional
memory, general enough to be used by many applications. We implemented one
such abstraction and called it bedrock. The failure model assumes
unwarranted interruptions as the main targeted risk (see 2.1
below). The bedrock currently serves as a foundation of the survivable,
available intermemory (see |www.intermemory.org|).
The bedrock is a simple transactional memory management system. It allows
complex updates to be enacted (committed, synced) atomically (at
once), over non-volatile block storage devices, such as hard drives, and to
persist from one sync to the next. If an intermediate series of updates
fails to commit, the previously committed state is guaranteed to be found in
where they it was left by the previous (successfully completed) commit. Any
such updates in progress after a commit can be aborted forcefully, and then
the previously committed state will likewise be ``magically'' reactivated.
Our solution consists of a disk block array and a mapping mechanism allowing for
two ``views'' of the blocks. The ongoing updates correspond to shadow
blocks, reflected in the shadow maps. The previously committed transaction
persists, its blocks intact, its maps current and safely in place, governed
by a single superblock. Once the updates are finished, they can be
committed with a single atomic write of the new superblock, which swaps the
current maps and the shadow ones. Each set of maps refers to their own blocks,
so formerly shadow blocks now also become current.
There are many transactional systems currently in use and under development,
described in the systems literature. Berkeley db system [SO92,BDB] provides a generalized transactional library. It relies on
logging, which bedrock avoids for efficiency and simplicity gain, at the
price of a smaller feature subset. The db provides transactional
functionality plus further database features, such as key-value extraction,
which in our system is implemented by the bxtree module sitting on top of
the bedrock. The db also relies on logging, which makes it RECNO mode
take longer than bedrock for most simple uses, but the efficient database
engine using caching helps the db in BTREE mode outperform the
bxtree/bedrock tandem. See 4 for the detailed experiments
comparing the performance of bedrock and db. SQRL, a free SQL project
for FreeBSD [Eva99], extends the notion of a transactional substrate
further to provide a transaction-based file system, a possible extension of
the bedrock itself (see the discussion at the end of this section).
Implementation
Since the superblock must be written atomically, its size should be the minimal
block size for any block device keeping it. The smallest device block size
known to the authors is 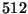 bytes, corresponding to a disk sector on some
systems. Our architectural assumptions for the operating system carrying the
bedrock are as follows:
bytes, corresponding to a disk sector on some
systems. Our architectural assumptions for the operating system carrying the
bedrock are as follows:
- Atomic write of the aligned atomic size data (512 bytes). Once the
write began, it must finish, or not begin at all. Most disk controllers
ensure when starting a write that it will go though even in the event of a
power failure [GP94].
- Aligned atomicity - a file write begins at an atomic write
boundary (see above). Thus, if we start to write a file by writing out an
atomic-size block, the write will indeed be atomic, and so will be all the
subsequent atomic-size writes.
- Non-volatile memory, e.g. on disk. Natural idea of non-volatile
memory means the data written to disk stays there until overwritten by a
knowing and willing user (no latent alterations by the OS).
- fsync(2) works. It means that memory-buffered files must be capable
of being flushed to disk at will using a system call such as Unix's
fsync(). The successful completion of the call guarantees the disk image is
what the user expects it to be, and if an interruption (see below) occurs
after an fsync(), all the data written before it will persist.
These assumptions allow us to build the bedrock system, capable of
withstanding the most typical system failures - interruptions, such as
power failures, disk sector failures, etc., including stacked ones. A good idea
of those interruptions covered by the bedrock protection can be gathered
from the NFS specification [NFSa,NFSb].
A bedrock file consists of a fixed number of homogeneous, fixed-size blocks.
It is the responsibility of an application to choose the number of blocks
n_blocks and a block size block_size before creating a bedrock,
and then manage its memory in terms of the blocks. Blocks can be allocated,
written, read, read, written, etc., and freed. The user deals with the block
addresses, which are simply numbers in the range 1 .. n_blocks.
Transactional semantics requires that certain mapping information, employed
by the mapping mechanism described below, is stored on disk as well.
Figure 1 shows the layout of a bedrock file in
non-volatile memory (on disk).
Figure:
Layout of a bedrock file in
non-volatile memory. Header consists of essential bedrock parameters and
mapping mechanism in fixed size segments, followed by the actual blocks.
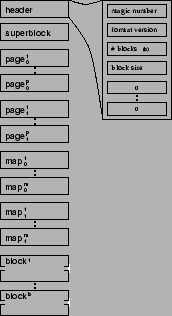 |
During a transaction, the original physical blocks can't be overridden
yet, until a commit or abort. A ``shadow'' physical block is
written instead. We separate the logical block addresses, given to the
users, from physical blocks, making a map array storing the
correspondence, much like virtual memory: map[logical] == physical
or is marked unallocated.
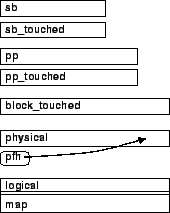
Figure 2 shows the memory
mapping structures.
Figure:
Memory layout of the
bedrock mapping mechanism. map[logical] == physical. The sb and
pps are bit vectors: bit sb[i] chooses pp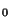 v. pp
v. pp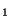 segment
of 4096 bits, in the range governed by
segment
of 4096 bits, in the range governed by 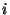 ; similarly bit pp[j] chooses
map
; similarly bit pp[j] chooses
map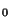 v. map
v. map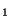 segment of 128 unsigned long physical entries (32
bits each) for the index range (of logical addresses) based on
segment of 128 unsigned long physical entries (32
bits each) for the index range (of logical addresses) based on 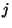 . The
touched bit vectors allow for selective writes of their ``parents'' upon
commit or abort. The free physical and logical array lists
(the latter sharing its array with map) allow for constant-time slot and
address allocation, respectively; physical_freed_head (pfh) protects
slots freed in the current transaction from reuse until a sync/abort.
. The
touched bit vectors allow for selective writes of their ``parents'' upon
commit or abort. The free physical and logical array lists
(the latter sharing its array with map) allow for constant-time slot and
address allocation, respectively; physical_freed_head (pfh) protects
slots freed in the current transaction from reuse until a sync/abort.
 |
Since we update only those portions of the map which actually changed, there's
no contiguous, full-size ``main'' or ``shadow'' arrays; rather, sector-size
groups of mapping entries serve as either in accordance with a ping-pong bit
flag in an upper-level mapping structure. The superblock contains 512 bytes
== 4096 bit flags, each capable of controlling an underlying mapping page.
Following the convention of grouping map entries into 512 byte segments, and
representing block addresses as |unsigned long| 4 byte entries, we have 128
entries per map segment. Should each superblock bit control (switch) a segment
directly, we would end up with only
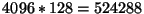 bottom-level blocks.
For some contemporary applications, such a low limit is insufficient, and the
number will seem only smaller in the future. Since we can't enlarge the
superblock without violating the atomicity condition, and the map entries and
their segment sizes are likewise fixed, we need to introduce an intermediate
mapping layer, which we call pages. Thus, the overall mapping becomes
three-level:
bottom-level blocks.
For some contemporary applications, such a low limit is insufficient, and the
number will seem only smaller in the future. Since we can't enlarge the
superblock without violating the atomicity condition, and the map entries and
their segment sizes are likewise fixed, we need to introduce an intermediate
mapping layer, which we call pages. Thus, the overall mapping becomes
three-level:
superblock 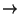 pages
pages 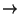 map
segments
map
segments
Naturally, each page will have the atomic size of 4096 bits, controlling just as
many bottom-level map segments. Each superblock bit now will govern one such
page. Thus, the total number of blocks switchable through our three-level
mapping scheme is
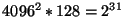 blocks. Given typical block sizes
starting at
blocks. Given typical block sizes
starting at 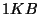 , this seems a reasonable supremum for some time to come. It
is important to notice that this supremum neatly fits into a typical four-byte
word of today, holding unsigned integer types with values as large as
, this seems a reasonable supremum for some time to come. It
is important to notice that this supremum neatly fits into a typical four-byte
word of today, holding unsigned integer types with values as large as
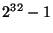 . Our supremum is the function of two assumptions - the atomic 512
byte sector size and 4 byte word, |unsigned long int| type representing block
addresses. (In the future, these architectural parameters are likely to change,
as the memory needs ever grow.) We maintain a version number, corresponding
to our bedrock format, in each bedrock file, so it can be properly
upgraded when the format evolves. The application must evaluate its needs ahead
of time and create the bedrock of sufficient size, planning both the
number of blocks and their size. Since every block overwritten during a
transaction requires a shadow block, the total number of blocks overwritten must
not exceed floor(
. Our supremum is the function of two assumptions - the atomic 512
byte sector size and 4 byte word, |unsigned long int| type representing block
addresses. (In the future, these architectural parameters are likely to change,
as the memory needs ever grow.) We maintain a version number, corresponding
to our bedrock format, in each bedrock file, so it can be properly
upgraded when the format evolves. The application must evaluate its needs ahead
of time and create the bedrock of sufficient size, planning both the
number of blocks and their size. Since every block overwritten during a
transaction requires a shadow block, the total number of blocks overwritten must
not exceed floor(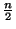 ).
).
We keep a single current version of the shadow mapping mechanism in the
memory record. All the three layers of mapping are present in a single instance
each - the superblock, the page array of (pages), and the map.
When an existing bedrock is open, these structures are assembled in memory
via a slalom procedure. First, the single superblock is read. Each bit
of it tells us, which corresponding page to read - since any of the two
versions can be current while the other is shadow, they have no preferential
names and are called simply 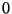 and
and 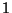 instances. The slalom proceeds by
filling each memory slot in the pages array from either
instances. The slalom proceeds by
filling each memory slot in the pages array from either 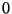 or
or 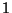 page
instance on disk, equaling the corresponding superblock bit. Once the single
``current'' page array is thus assembled, the slalom repeats for the map
itself - its segments are recalled from either
page
instance on disk, equaling the corresponding superblock bit. Once the single
``current'' page array is thus assembled, the slalom repeats for the map
itself - its segments are recalled from either 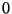 or
or  disk instances,
depending on the value of the controlling bit within the responsible page
now.
disk instances,
depending on the value of the controlling bit within the responsible page
now.
Just upon the slalom assembly, the superblock, pages and map faithfully reflect
the ``current'' state of the superblock. Any write operations, however, will
reserve their ``shadow'' blocks, and update the map, tainting the map segments
involved as touched. The ``shadow'' map segments will go into the slots
opposite of those they were read from during the slalom, and as the slalom
assembly was governed by the page bits, the touched page bits must be
flipped, too, in the ``shadow'' pages. Similarly to map/page bit flip, enacting
the updated page will flip its bit in the superblock. The final superblock is
thus prepared, ready for the final slide-in. Finalizing the commit
requires that the operating system synchronizes its view of the file with that
assumed by the bedrock module (for instance, on Unix, the fsync system
call is provided to flush the buffers to disk). The actual slide-in calls
fsync twice - immediately before and immediately after writing out the new
superblock.
The slalom is the most important bedrock operation, and it has been
abstracted and parameterized for three different occasions: read, write,
and abort. It works in cooperation with the touched arrays of flags,
and is at the core of bedrock open, sync (commit), and abort
operations. The touched flags, set naturally when allocating and
overwriting blocks, let us write/re-read out only those parts of the
maps and pages which were actually updated. We also set all bits of all
touched arrays before an open, then simply make a slalom read, which
consequently refills all the maps and the superblock. Also, since the
touched arrays accurately record all of the bit flags changed, we don't need
to read anything but the map itself when aborting!
Within the bedrock_slalom function, this ternary parameter is divided into
two boolean flags, reading and aborting. Then, the slalom goes as
follows:
- When reading, the superblock is read in first, since it has to govern
the slalom-gathering of the pages.
- The superblock is then traversed: when
- reading, the disk-current pages are read in accordance with
the disk superblock - pages come from the current slots, those
specified in the current superblock (just read). The page touched
flag is reset for each page being read.
- writing, the disk-shadow pages are written in accordance with
the shadow, i.e. memory superblock - pages go to the shadow
slots, as opposed to the current ones recorded in the disk superblock
- aborting, the shadow, i.e. memory, superblock bits touched
during the transaction being aborted are simply reversed if they were set
during it in sb_touched.
As each page is read, its governing sb_touched bit is reset.
- Similarly, the pages are now traversed, and if aborting, simply
restored by reversing those bits set in pp_touched (ping-pong pages
touched bits). The maps should be read back from the disk when aborting, as
the original modified slots are overwritten in memory with the shadow ones.
The rest is analogous to the superblock traversal.
- Finally, in case of writing, the slide-in sequence, described above,
is executed (fsync
 write superblock
write superblock  fsync).
fsync).
Each write is given a logical address to write and a pointer to a memory
buffer going to the bedrock under that address. The write checks first,
whether the physical slot, already associated with the logical address given,
was assigned in a previous transaction. If so, it has to be preserved, and a
shadow slot is found for use in the course of this transaction. Such shadow
block protection should not be done twice for a logical address which
already was written during this transaction.
We envision several important extensions to bedrock, namely (i)
parallel/nested transactions, (ii) multiple time-views (``old'' v. ``new''),
(iii) bedrock-based file systems, (iv) in-block checksums and
inter-block ``RAID'' error correction, (v) superblock redundancy, (vi)
bedrock block device, controlling a raw partition, (vii) memory caching
with (viii) transparent in-memory block packing/unpacking. These extensions
will be discussed in detail in a journal version of this work.
Synchronizable Databases
In this section, we first formally describe a synchronizable database as
an abstract data-type. We then describe our implementation of the abstraction,
which consists of two separate modules - the bxtree module and the
osynch module.
A synchronizable database 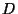 is a set containing records of the
form
is a set containing records of the
form 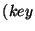 ,
, 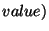 . The
. The 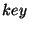 field takes values from a totally-ordered set
field takes values from a totally-ordered set
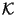 of keys. Any key in
of keys. Any key in 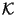 occurs in
occurs in 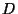 at most once.
at most once.
The major operations supported by a synchronizable database as an abstract data type are insertion,
deletion and retrieval of records, and a range synchronization operation.
The first three are standard operations on databases with records. The last one, unique to synchronizable
databases, is specified below.
The input to a range synchronization operation is an interval 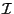 of
of
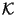 and two databases
and two databases 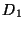 and
and 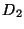 . The
operation basically tries to make the restrictions of
. The
operation basically tries to make the restrictions of 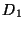 and
and 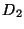 to
to
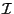 identical. In particular, it identifies three sets of keys, which
we call the discrepancy sets
identical. In particular, it identifies three sets of keys, which
we call the discrepancy sets 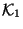 ,
, 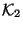 and
and
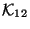 . These three sets are all subsets of the key interval
. These three sets are all subsets of the key interval 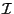 .
Discrepancy set
.
Discrepancy set 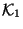 is the set of keys in
is the set of keys in 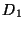 which are not in
which are not in
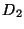 ,
, 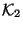 is the set of keys in
is the set of keys in 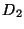 which are not in
which are not in 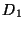 , and
, and
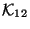 is the set of keys which are in both
is the set of keys which are in both 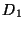 and
and 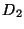 but whose
corresponding records in the two databases differ in the
but whose
corresponding records in the two databases differ in the 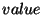 field. The
operation calls different handler functions for each of these three
sets. Typically, the handler functions for
field. The
operation calls different handler functions for each of these three
sets. Typically, the handler functions for 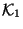 and
and 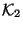 would copy the missing records from one database to the other. The handler
function for
would copy the missing records from one database to the other. The handler
function for 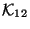 would typically, for each key in the discrepancy
set, compare the records in
would typically, for each key in the discrepancy
set, compare the records in 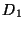 and
and 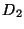 that have the key and replace one
of them with the other3.
that have the key and replace one
of them with the other3.
In this section, we describe a B+-tree based implementation of synchronizable
databases. The main power of the synchronizable databases abstraction lies in
the range synchronization operation. Thus, we separate our implementation into
two independently usable modules - the bxtree module and the osynch module. The
two modules talk to each other through a very clean interface consisting of just
two functions.
The bxtree (or extended B-tree) module implements a B+-tree based database
engine augmented with a couple of functions for supporting range
synchronization. For example, a typical operation on the database would input a
key range (i.e. an interval of the space of keys) and return a short summary4 of all the records in the database whose keys lie in the
given key range. In a B+-tree, the records are stored only in the leaves, and
all the leaves are at the same height in the tree. In our implementation, with
each record a fixed size digest of the record is also stored. And each
internal node also stores, for each of its children, the XOR of the
digests of all the records in the subtree rooted at the child. Note that since
XOR is an associative operation, this information can be efficiently
maintained across tree-rebalancing operations. Because of these digests stored
in the internal nodes, interval summary computation operations (like the one
illustrated above) can be performed in time proportional to the height of the
tree.
The osynch (or object synchronization) module, implements the range
synchronization operation on bxtree databases. Our implementation is specially
tuned for the case when the databases being synchronized are located on
different processors connected via a limited bandwidth link. Thus, one of the
goals is to try to minimize the network traffic generated by the synchronization
operation. The synchronization operation works in a number of communication
rounds. In each round, the key range of interest is partitioned into smaller
sub-ranges. For each sub-range, the two databases compute the summary of
records lying in that sub-range and one of the databases sends its summaries to
the other side. The corresponding summaries from the two sides are compared and
the operation is recursively applied to sub-ranges whose summaries do not match.
Only those records are transferred from one side to the other which (1) are
missing on the other side, or (2) have a mismatching record on the other side.
Thus, unnecessary transfer of large amounts of data is prevented.
The Bxtree Module
On an abstract level, the bxtree module simply implements a database engine for
storing and managing records of the form 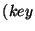 ,
, 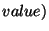 , enhanced with some
support for range synchronization. It provides functions for insertion, deletion
and retrieval of records. In addition to these, it provides the following two
functions which are used by the osynch module for implementing the range
synchronization operation.
, enhanced with some
support for range synchronization. It provides functions for insertion, deletion
and retrieval of records. In addition to these, it provides the following two
functions which are used by the osynch module for implementing the range
synchronization operation.
- Get_All_Hashes:
- The input is an interval
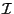 of
of 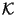 . The
output is a list of pairs of the form
. The
output is a list of pairs of the form 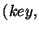
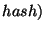 . The list has one pair
for each record in the database whose
. The list has one pair
for each record in the database whose 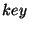 field belongs to
field belongs to 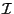 . The
first element in the pair is the
. The
first element in the pair is the 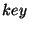 field of the record, and the second
element is a fixed size digest of the record. If the database has no
record with
field of the record, and the second
element is a fixed size digest of the record. If the database has no
record with 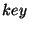 field belonging to
field belonging to 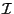 , an empty list is returned.
, an empty list is returned.
- Get_Interval_Hashes:
- The input is an interval
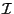 of
of 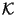 and a positive integer
and a positive integer 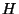 . The function partitions
. The function partitions 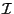 into at
most
into at
most 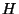 disjoint sub-intervals and returns a list of triplets of the form
disjoint sub-intervals and returns a list of triplets of the form
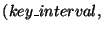
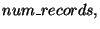
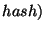 . The list has one triplet for each
sub-interval. The first element of the triplet is the sub-interval itself; the
second and third elements are, respectively, the number and a fixed size digest of all the records in the database whose
. The list has one triplet for each
sub-interval. The first element of the triplet is the sub-interval itself; the
second and third elements are, respectively, the number and a fixed size digest of all the records in the database whose 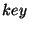 fields belong to the
sub-interval. Whether the database has any records with
fields belong to the
sub-interval. Whether the database has any records with 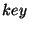 field belonging
to
field belonging
to 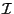 or not, the list returned is always non-empty and the
sub-intervals in the list form a disjoint partition of
or not, the list returned is always non-empty and the
sub-intervals in the list form a disjoint partition of 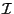 .
.
Our implementation of the bxtree module uses the B+-tree data structure for
storing records. The internal nodes of the tree form an index over the leaves of
the tree where the real data resides. In the leaf nodes where the records are
stored, a fixed size digest5 is also stored for each record. This digest is used (1)
to verify record integrity, and (2) by functions providing support for range
synchronization. Each internal node stores a set of keys to guide the search
for records. In addition, for each of its children, it stores a triplet of the
form 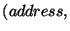
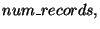
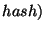 where
where 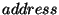 is the address of the
child node,
is the address of the
child node, 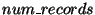 is the number of records in the child's sub-tree, and
is the number of records in the child's sub-tree, and
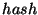 is the XOR of the digests of the records in the child's subtree.
Since XOR is an associative operation, this information can be
efficiently maintained across tree-rebalancing operations.
is the XOR of the digests of the records in the child's subtree.
Since XOR is an associative operation, this information can be
efficiently maintained across tree-rebalancing operations.
The database allows different records to have 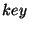 and
and 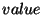 fields of
different sizes. This affects the structure of the tree in several ways. We
store each node of the tree in a separate bedrock block. Since all bedrock
blocks are of the same size (in bytes), each node gets the same number of bytes
of storage. Thus, two full leaf nodes can have different number of
records. Similarly, two full internal nodes can have different number of
keys and hence different fan-out. Hence, the property (which regular B+-trees
with keys and records of fixed size exhibit) that the fan-out of any two
non-root internal nodes in the tree can not differ by more than a factor of 2,
is not exhibited by the tree in our implementation.
fields of
different sizes. This affects the structure of the tree in several ways. We
store each node of the tree in a separate bedrock block. Since all bedrock
blocks are of the same size (in bytes), each node gets the same number of bytes
of storage. Thus, two full leaf nodes can have different number of
records. Similarly, two full internal nodes can have different number of
keys and hence different fan-out. Hence, the property (which regular B+-trees
with keys and records of fixed size exhibit) that the fan-out of any two
non-root internal nodes in the tree can not differ by more than a factor of 2,
is not exhibited by the tree in our implementation.
In a regular B+-tree, a node underflows when the number of records (or
keys) in it is less than half the maximum number. And it is always possible to
handle underflow by either borrowing from or merging with siblings. This leads
to the guarantee that each non-root node will be using at least 50% of the
space allocated to it. In our implementation of B+-tree, since different
records are allowed to have 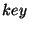 and
and 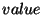 fields of different sizes, the
50% space efficiency guarantee is difficult to achieve. This happens because of
the basic bin-packing kind of phenomenon. For example, when a node is split due
to an overflow resulting from an insertion, it might not be possible to split it
into two nodes that are both at least 50% full. Similarly, when the space usage
of a node falls below 50% during a deletion, it is possible that both borrowing
and merging fail to handle the underflow. It turns out that if we have an upper
bound on the sizes of the records in terms of the size of the bedrock blocks
used for storing the nodes, we can provide a space utilization guarantee
of something less than 50%. For example, with the constraint that no record
occupies more than a tenth of a bedrock block, we can achieve a storage
utilization guarantee of 40%. Due to a technical difficulty, arising out of
our use of variable length encodings for storing integers, we are forced to
leave some storage (
fields of different sizes, the
50% space efficiency guarantee is difficult to achieve. This happens because of
the basic bin-packing kind of phenomenon. For example, when a node is split due
to an overflow resulting from an insertion, it might not be possible to split it
into two nodes that are both at least 50% full. Similarly, when the space usage
of a node falls below 50% during a deletion, it is possible that both borrowing
and merging fail to handle the underflow. It turns out that if we have an upper
bound on the sizes of the records in terms of the size of the bedrock blocks
used for storing the nodes, we can provide a space utilization guarantee
of something less than 50%. For example, with the constraint that no record
occupies more than a tenth of a bedrock block, we can achieve a storage
utilization guarantee of 40%. Due to a technical difficulty, arising out of
our use of variable length encodings for storing integers, we are forced to
leave some storage (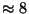 bytes) unused in each bedrock block. This
will constitute a tiny fraction of the total space in any reasonable use of the
bxtree module.
bytes) unused in each bedrock block. This
will constitute a tiny fraction of the total space in any reasonable use of the
bxtree module.
The insertion, deletion and retrieval operations are implemented in a manner
similar to regular B+-trees. The non-regularity of sizes in our implementation
leads to several interesting cases which do not occur in the case of regular
B+-trees, and which need careful handling. A typical example is the case where a
deletion causes some nodes to split and consequently, the height of
the tree increases6.
The number of nodes (or equivalently the number of bedrock blocks) accessed by
an operation is a good measure of the amount of time taken. So for each
operation, we will only estimate the number of nodes accessed. The insertion,
deletion and retrieval operations make 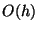 node accesses where
node accesses where 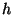 is the
height of the tree.
is the
height of the tree.
The Get_All_Hashes function is a simple recursive function having leaf nodes
as the base case. The input to the function is an interval 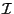 in the
totally-ordered space of keys. A leaf node is said to be relevant for
in the
totally-ordered space of keys. A leaf node is said to be relevant for
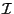 if it contains a record with
if it contains a record with 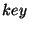 field belonging to
field belonging to  , or
if it is adjacent to a node like that in the left-to-right ordering of the leaf
nodes. By this definition, the function only accesses the nodes that are
relevant for
, or
if it is adjacent to a node like that in the left-to-right ordering of the leaf
nodes. By this definition, the function only accesses the nodes that are
relevant for 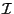 , and their ancestors. Thus it makes
, and their ancestors. Thus it makes 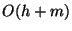 node
accesses where
node
accesses where 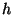 is the height of the tree and
is the height of the tree and 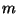 is the number of leaf nodes
relevant for
is the number of leaf nodes
relevant for 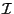 . Clearly, the size of the output list is an upper bound
on
. Clearly, the size of the output list is an upper bound
on 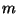 .
.
The Get_Interval_Hashes function is most interesting. The function is
supposed to partition the given key interval into sub-intervals and return a
summary for each sub-interval. It turns out that it helps the osynch module to
have the sub-intervals such that the database contains almost equal amount of
data in each of the sub-intervals. We use the balance in the tree in a
natural way to construct such a partition. The input to the function is a key
interval 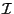 , and an upper bound
, and an upper bound 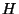 on the number of sub-intervals in
the partition. The function is implemented in a recursive fashion. A typical
instance of the function works with an internal tree node
on the number of sub-intervals in
the partition. The function is implemented in a recursive fashion. A typical
instance of the function works with an internal tree node 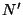 , a key interval
, a key interval
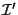 and integer bound
and integer bound 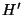 . First, it identifies the set
. First, it identifies the set 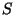 of relevant children (i.e. children whose subtrees contain nodes relevant for
of relevant children (i.e. children whose subtrees contain nodes relevant for
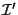 . See above for the definition of relevance.) The children of
. See above for the definition of relevance.) The children of
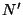 are sorted in a natural left-to-right order. We observe that the children
in
are sorted in a natural left-to-right order. We observe that the children
in 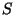 are consecutive in this left-to-right order. The function, then,
partitions
are consecutive in this left-to-right order. The function, then,
partitions 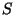 into
into
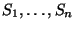 (with
(with
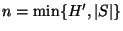 ) where
each
) where
each 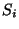 consists of some children in
consists of some children in 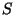 that are consecutive in the
left-to-right order. The partition is done in such a way that each
that are consecutive in the
left-to-right order. The partition is done in such a way that each 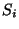 has
almost the same number of children from
has
almost the same number of children from 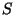 . This partition of
. This partition of 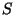 naturally
leads to a partition of
naturally
leads to a partition of 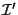 into sub-intervals
into sub-intervals
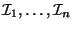 , where
, where 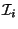 corresponds to
corresponds to 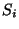 . The end-points of the
sub-intervals come from the set of keys stored in
. The end-points of the
sub-intervals come from the set of keys stored in 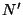 , except that the left
(right) end-point of
, except that the left
(right) end-point of 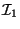 (
(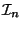 ) is same as the left (right)
end-point of
) is same as the left (right)
end-point of 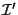 . The bound
. The bound 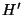 is also partitioned into
is also partitioned into
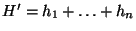 with no two
with no two 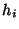 's differing by more than one. Then for each
's differing by more than one. Then for each 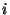 ,
working on the children in
,
working on the children in 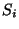 (recursively or otherwise, depending on whether
the children are leaf nodes or not), a partition of
(recursively or otherwise, depending on whether
the children are leaf nodes or not), a partition of 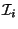 into at most
into at most
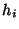 sub-intervals is obtained. The output list for
sub-intervals is obtained. The output list for 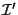 is formed by
concatenating the sublists from each of the
is formed by
concatenating the sublists from each of the 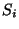 's. As described earlier,
's. As described earlier, 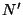 stores a triplet of the form
stores a triplet of the form 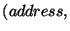
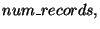
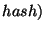 for each of its
children. The
for each of its
children. The 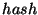 fields for some of the children in
fields for some of the children in 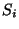 are used when
are used when
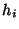 is 1.
is 1.
Again the function accesses only a portion of the sub-tree formed by leaf nodes
relevant for 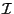 and their ancestors. It makes
and their ancestors. It makes 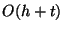 node accesses
where
node accesses
where 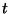 is a number bounded from above by the size of the output list.
is a number bounded from above by the size of the output list.
Our implementation of bxtree also stores an integral field called version
with each record. Thus, a record is really a triplet of the form 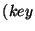 ,
,
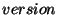 ,
, 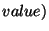 , although conceptually the version field can be
thought of as part of the value field. The version field can be
used by the handler functions that are invoked by the osynch module. For
example, the version field can be used to keep track of the revisions made
to the value field of a record, and then the handler function for
, although conceptually the version field can be
thought of as part of the value field. The version field can be
used by the handler functions that are invoked by the osynch module. For
example, the version field can be used to keep track of the revisions made
to the value field of a record, and then the handler function for
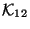 can decide to replace the record with a smaller version field
(indicating a stale value field) by the other one with a larger version
(indicating a more fresh value field.)
can decide to replace the record with a smaller version field
(indicating a stale value field) by the other one with a larger version
(indicating a more fresh value field.)
The Osynch Module
This module implements the range synchronization operation for bxtree databases.
As described earlier, our implementation is designed for the case where the two
databases are not located on the same processor. The two databases are assumed
to be located on different processors connected via a limited bandwidth link.
Thus, a major goal here is to try to minimize the traffic generated by the
synchronization operation.
In most situations, however, it is also desirable to minimize (or at least keep
within reasonable limits) the number of communication rounds taken by the
synchronization protocol. Our synchronization algorithm tries to achieve both
of these objectives. An interesting related work is the rsync algorithm
from [TM96] which addresses the synchronization problem for
unstructured text/binary files. There has also been some recent theoretical work
on the synchronization. See [E99] and [Or93]
for example.
The naive approach of bringing portions of one database to the other and then
doing a synchronization is too inefficient. Instead, in our implementation only
summaries7 of portions of one database are sent across the network in
order to identify the discrepancies. Once the discrepancies are identified, only
those records are transferred which need to be transferred to make the databases
synchronized.
Our implementation of the synchronization operation is asymmetric in the
sense that it sees one database as a local database and the other one as a
remote database. It is assumed that local database can be accessed with no
(or minimal) network traffic, whereas remote database accesses generate network
traffic. This asymmetric view allows the module to make optimizations that
minimize network traffic. Typically, the synchronization operation will be used
by a processor to synchronize its local database with some remote database.
The synchronization algorithm is fairly simple. The algorithm starts by asking
both databases to compute a single summary of all records lying in the
given key interval. The Get_Interval_Hashes function is invoked for this. The
remote summary is transferred to the local side and compared with the local
summary. If the summaries match, it is concluded that the databases are already
synchronized restricted to the given key interval. Otherwise the size of the
remote database restricted to the given key interval is checked. If the remote
database only has a small number of records lying in the key interval, then
digests for all those individual records are transferred from the remote to the
local side (the Get_All_Hashes function is invoked here), and a
record-by-record comparison is made to identify discrepancies. Otherwise the
remote database is asked (by calling the Get_Interval_Hashes function) to
partition the key range into smaller sub-intervals and send summaries for each
of the sub-intervals. These remote summaries are then compared against
corresponding local summaries and the operation is invoked recursively for
sub-interval whose summaries do not match.
The synchronization operation takes at most 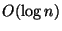 communication rounds to
identify each discrepancy, where
communication rounds to
identify each discrepancy, where 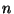 is the total size of the two databases
restricted to the given key interval. Thus, the total number is communication
rounds is
is the total size of the two databases
restricted to the given key interval. Thus, the total number is communication
rounds is 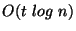 , where
, where 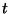 is the combined size of the three
discrepancy sets. Also, since all bxtree operations take time proportional to
the height of the tree, the overall computational burden for the synchronization
operation is
is the combined size of the three
discrepancy sets. Also, since all bxtree operations take time proportional to
the height of the tree, the overall computational burden for the synchronization
operation is
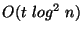 .
.
In practice however, the number of rounds taken and the network traffic
generated depend on several factors including how the discrepancies are
distributed across the entire key range and how the parameters in the algorithm
are chosen. There are two main parameters in the synchronization algorithm which
need to be carefully chosen. The first one determines when to invoke the
Get_All_Hashes operation instead of further partitioning with the
Get_Interval_Hashes operation. The second parameter determines the number of
partitions obtained through calls to Get_Interval_Hashes. The choice of these
parameters to a very large extent determines the actual network traffic
generated and the number of communication rounds taken. For example, if the
algorithm decides to invoke the Get_All_Hashes function on key intervals for
which the remote database has huge number of records, then the number of
communication rounds would be small but every round would generate heavy network
traffic. Similarly, if the Get_All_Hashes function is invoked only on very
small key intervals, then the number of rounds will be large. Note that the
objective of the synchronization protocol is not only to minimize the amount of
network traffic generated, but also to keep the number of communication rounds
within reasonable limits. These two objectives often compete with each other.
Thus, the two parameters above need to be tuned to suit different applications
and conditions.
Theoretically it is possible that on some input, the osynch algorithm fails to
detect some discrepancy and hence does not really synchronize the databases.
There are two factors that can contribute to such an error. First is our use of
the MD5 hash function for computing the digests. There are collisions (some of
which are known) for the MD5 hash function. Thus it is possible that two
different records yield the same digest. The second factor is our use of the XOR
function for combining the digests from different records. It is quite possible
that two different sets of digests yield the same result when digests in each of
them are XORed together. Still quite arguably, the probability of an error
arising out of these two factors is very small (but positive) and can be
ignored. Hashes have been commonly used for identifying changes in huge amounts
of data. See [LLS99] for example.
An interesting direction for further exploration is to try out associative
functions other than XOR and upper bound the error probability with those
functions. The error probability can be further reduced by using more than one
digests. In other words, the summary used by the synchronization algorithm
could contain a set of digests as opposed to just one digest. The rsync
algorithm from [TM96] uses two digests, one cryptographically strong
but hard to compute and the other cryptographically weak but easy to compute.
Experiments
We tested the bedrock, bxtree and osynch modules extensively
together and separately, and compared them to Berkeley DB ([BDB],
referred below as db) - an industrial-strength transactional database
supporting transactions and B+-tree access mode.
The first bedrock experiment measures the performance of its transactional
mechanism. Our simple driver creates a bedrock of a fixed size, and then
runs a series of transactions, overwriting ever increasing fractions of the
bedrock, from 0 to 0.5, in 20 increments. For each fraction, we run 10
transactions of that size, overwriting the number of bedrock blocks
corresponding to the fraction, and average the times to report a single time for
that fraction.
The comparable mode for db is RECNO with the transactional support turned
on. The performance of both systems is reflected in Figure
3.
Figure:
bedrock transactional management is compared to the Berkeley db
transactional subsystem. A series of transactions is run, their size
incremented from 0 to 0.5 of the bedrock file size in 20 increments. For
each fraction, 10 transactions are run and the average time plotted. Both
systems achieve optimal linear performance, while the simpler bedrock
leads by a factor of 9.
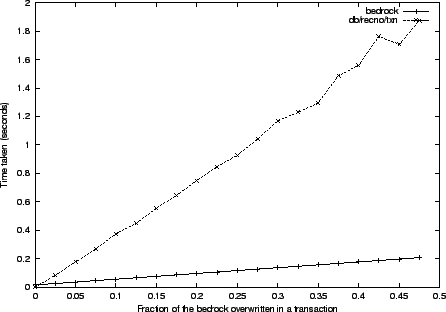 |
Both db and bedrock achieve linear performance (db uses logging,
which may require extra management from time to time). Since db is a
general embedded database system, it does much more than bedrock, which may
explain the constant factor by which the bedrock is faster. The db
database is created by the insertions we measure, and grows from zero size to
the maximum, while the size of the bedrock file remains fixed at its
maximum. All experiments, unless stated otherwise, are performed on a
dual-Pentium II 400 MHz machine with 512 MB of RAM and an 8 GB RAID array of
hard drives.
The second bedrock experiment tested the ``overhead'' from using the
bedrock as a transactional foundation in an application such as bxtree.
The real bedrock consistently differs from the dummy one by a
constant factor of only about 1.15, which shows that the overhead of
using our transactional system is minimal. (The benefit, of course,
is having a crash-proof disk image of any memory data structure, which
would justify a much larger factor for safety-critical applications.)
Performance of the bedrock I/O much depends on the underlying Unix
operations, read(), write(), and fsync(). The I/O can be sped up if
bedrock is implemented as a device controlling a raw partition directly,
which is greatly facilitated by its low-level structure of an array of
fixed-size blocks.
Another tandem bxtree/bedrock experiment compares the throughput of each
system when making a large number of random insertions in a pre-created
database. For our experiment, we first created a database by making 1 million
random insertions, and then measured the time necessary to perform 10,000 more
insertions, in 1,000 increments.
The records are 1,000 byte long, with 100 byte keys and 900 byte values. We
sync/commit after every 10 insertions. In order to reflect the
bedrock semantics, where the database file is self-contained, we performed
db check-pointing after every transactional commit. The experiment
plotted in Figure 4 is done on a machine with 256 MB of
RAM.
Figure:
bedrock transactional management is compared to the Berkeley db
transactional subsystem. A series of transactions is run, their size
incremented from 0 to 0.5 of the bedrock file size in 20 increments. For
each fraction, 10 transactions are run and the average time plotted. Both
systems achieve optimal linear performance, while the simpler bedrock
leads by a factor of 9.
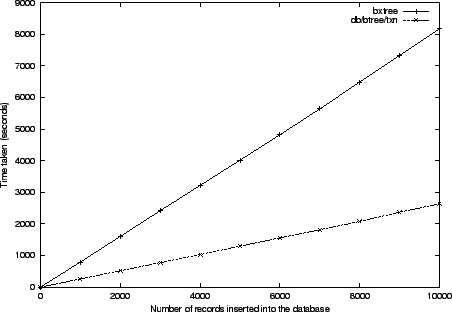 |
The initialization of the database (the original one million insertions,
roughly) took about 112,000 seconds for bxtree/bedrock and about 38,000
seconds for db. When the same experiment is repeated on the machine with
twice the RAM, 512 MB, we get the measured 10,000 insertions in 2,360 seconds
for bxtree/bedrock versus 385 seconds for db. The initialization
then takes 104,000 v. 12,500 seconds, respectively.
Varying the RAM size shows how the database performance depends on caching.
Since db uses memory pools extensively, its performance drastically
depends on the RAM size of the machine used in the measurements. On the
contrary, the bxtree/bedrock system was designed for mission-critical
applications to have a minimal memory footprint and a preallocated fixed set of
verified resources, namely the disk file of the maximum size which doesn't grow
and is preformatted before use. Employing caching would allow us to overcome
the factor of 3-4 by which our system now differs from the db. Given more
memory, upper levels of the bxtree could be stored there all the time, ready
for immediate use. Currently, bxtree nodes are stored in bedrock blocks
after being processed by another LIBPA module, BMSG, which packs
various fields into cohesive binary blocks. Every time a bxtree bedrock
block is read, the nodes are unpacked back. BMSG architecture allows us to
abstract from the actual binary layout of a bxtree node. On the other hand,
extra processing is involved in every I/O operation, which can be saved when
more of the bxtree nodes remain in memory in their raw, unpacked form.
The experiments show the effectiveness of the bxtree/bedrock system.
Its performance is linear in the number of database operations, which is
optimal, and differs from an industrial db system only by a constant factor
due to different memory models. With the improvements outlined above, the
bxtree/bedrock system provides a solid, efficient building block for
synchronizable transactional databases, ready for use by such modules as the
osynch.
In this section, we describe an experiment where two processes running on
different machines synchronize their databases with each other. We call the two
processes the master and the slave processes. Both processes begin
with an initial database of 30000 records each. Their initial databases are
identical. The initial database was pseudo-randomly generated by inserting 30000
different (pseudo-randomly created) records one by one into an empty database.
All records in the experiment consist of a 100 byte key and a 1900 byte
value field. After initialization, the two processes add another fixed
number (which we denote by  ) of records into their respective databases. The
additional records are also pseudo-randomly generated, but the master and the
slave processes are forced to create different sets of records. Thus, at this
point both databases have 30000 +
) of records into their respective databases. The
additional records are also pseudo-randomly generated, but the master and the
slave processes are forced to create different sets of records. Thus, at this
point both databases have 30000 +  different records, and the two databases
agree on only 30000 of them.
different records, and the two databases
agree on only 30000 of them.
Now, the master process starts the synchronization protocol to synchronize its
entire database with the slave's database. The discrepancy handler
functions used for synchronization do the trivial job of transferring the
missing records from one side to the other. In our experiment, by design, there
are no mismatch discrepancies.
Figure:
The figure describes an experiment
where two processes running on different machines synchronize their databases
with each other. The databases contain 30000 +  records each, but the two
databases agree on only 30000 of them. Thus, each database is missing
records each, but the two
databases agree on only 30000 of them. Thus, each database is missing 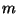 records that the other database possesses. The vertical axis shows the number
of communication rounds taken by the synchronization protocol to identify all
the discrepancies. The horizontal axis shows the values of
records that the other database possesses. The vertical axis shows the number
of communication rounds taken by the synchronization protocol to identify all
the discrepancies. The horizontal axis shows the values of 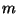 for which the
experiment was run. As expected, the relationship is linear.
for which the
experiment was run. As expected, the relationship is linear.
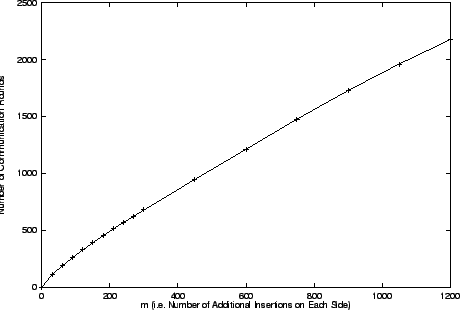 |
The graph in Figure 5 plots the number of communication
rounds taken by the synchronization protocol to identify all the discrepancies
against 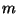 . Remember that
. Remember that 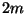 is the total size of the discrepancy sets.
is the total size of the discrepancy sets.
Figure:
For the same experiment as described by the previous figure,
this graph plots the network traffic generated (in bytes) by the
synchronization protocol to identify the discrepancies against 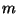 . This does
not include the network traffic generated by the discrepancy handler
functions for transferring the missing records between the databases.
. This does
not include the network traffic generated by the discrepancy handler
functions for transferring the missing records between the databases.
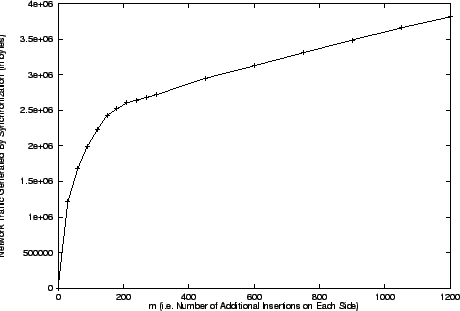 |
Figure 6 shows the network traffic generated by the
synchronization operation while identifying the discrepancies. This does not
include the traffic generated by the discrepancy handlers for transferring the
missing records between the two sides. As expected, the graph is asymptotically
linear.
We have introduced the abstract notion of a synchronizable
transactional database, and both described and implemented a novel
three-layer design that realizes it. Beyond implementation our
experimental measurements confirm the basic ideas and analysis of our
design, and that our system as-is represents a practical solution to
the synchronization problem. Our experimental comparisons with
Berkeley DB reveal that our bedrock layer is a much more efficient
alternative for simple transactional block storage applications.
While our combined bxtree/bedrock system perform well (and as
expected) when compared with Berkeley DB performing traditional
operations (not synchronization), it is nevertheless somewhat slower
and points to the need for in-memory B+-tree block management in our
system. This work is under way.
-
- CEG+99
-
Yuan Chen, Jan Edler, Andrew Goldberg, Allan Gottlieb, Sumeet Sobti, and Peter
Yianilos.
A prototype implementation of archival intermemory.
In Proceedings of the fourth ACM Conference on Digital libraries
(DL '99), 1999.
- Eva99
-
Jason Evans.
Design and implementation of a transaction-based filesystem on
FreeBSD.
In Proceedings of the USENIX Annual Technical Conference,
Monterey, California, 1999. USENIX Association, 1999.
Electronic version: http://www.usenix.org/publications/library/proceedings/usenix99/evans.html.
- GY98
-
Andrew V. Goldberg and Peter N. Yianilos.
Towards an archival intermemory.
In Proc. IEEE International Forum on Research and Technology
Advances in Digital Libraries (ADL'98), pages 147-156. IEEE Computer
Society, April 1998.
- GP94
-
Gregory R. Ganger and Yale N. Patt.
Metadata update performance in file systems.
In Proceeding of the First USENIX Symposium on Operating Systems
Design and Implementation (OSDI), Monterey, California, 1999. USENIX
Association, 1994.
- GR92
-
Jim Gray and Andreas Reuter.
Transaction Processing: Concepts and Techniques.
Morgan Kaufmann, 1992.
- NFSa
-
RFC 1094, NFS: Network File System Protocol Specification (v2).
Technical report.
Electronic version: ftp://ftp.isi.edu/in-notes/rfc1094.txt
- NFSb
-
RFC 1813, NFS Version 3 Protocol Specification.
Technical report.
Electronic version: ftp://ftp.isi.edu/in-notes/rfc1813.txt
- BDB
-
Berkeley db.
http://www.sleepycat.com/
- SO92
-
Margo Seltzer and Michael Olson.
LIBTP: Portable, modular transaction for Unix.
In USENIX Winter Conference. USENIX Association, 1992.
Electronic version: http://www.eecs.harvard.edu/ margo/papers/libtp.ps.gz.
- CG97
-
Arturo Crespo and Hector Garcia-Molina.
First European Conference on Research and Advanced Technology
for Digital Libraries, Pisa, Italy, Sept 1997.
Published in Lecture notes in computer science; Vol. 1324, pages 147-71.
Springer-Verlag.
- E99
-
Alexandre V. Evfimievski.
A probabilistic algorithm for updating files over a
communication link.
Proceedings of the ninth annual ACM-SIAM symposium on Discrete
Algorithms, Baltimore, Jan 1998. Pages 300 - 305.
- LLS99
-
Yui-Wah Lee, Kwong-Sak Leung and Mahadev Satyanarayanan.
Operation-based Update Propagation in a Mobile File System.
Proceedings of the USENIX Annual Technical Conference,
Monterey, California, June 1999.
- Or93
-
A. Orlitsky.
Interactive communication of balanced distributions and of correlated files.
SIAM J. of Dis. Math, 6:4, pp. 548-564, November 1993.
- TM96
-
A. Tridgell and P. Mackerras.
The rsync algorithm.
Technical Report TR-CS-96-05, The Australian National
University. Available from http://samba.anu.edu.au/rsync/, June 1996.
A Synchronizable Transactional Database
This document was generated using the
LaTeX2HTML translator Version 2002 (1.62)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -image_type gif -nonext_page_in_navigation -noprevious_page_in_navigation -up_url ../main.html -up_title 'Publication homepage' -numbered_footnotes sdb.tex
The translation was initiated by Peter N. Yianilos on 2003-10-10
Footnotes
- ... Yianilos1
-
The authors are listed in alphabetical order. The first author is
with the University of Washington, and the second with the
University of Pennyslvania. The third author is
affiliated with Netrics.com, and is currently also a visitor to the
Princeton University Computer Science Department. Direct
correspondence to the third author at pny@cs.princeton.edu.
- ... file2
- Support
for raw disk partitions is planned
- ... other3
- As described in a later section, our
implementation of synchronizable database also maintains for each record a
field called version. This field can be used by the handler function
for
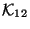 to decide which record to replace with the other.
to decide which record to replace with the other.
- ... summary4
- The summary would typically contain a digest of the
records of interest.
- ... digest5
- We use the well known MD5 algorithm to
compute the digest.
- ...increases6
- When an underflowing node borrows
records or keys from its siblings, the key in its parent that separated it
from its sibling changes. The new key that goes to the parent might be larger
than the previous key, thus causing the parent to split. The split can result
in more splits and an eventual increase in the tree height.
- ...
summaries7
- In our implementation, the summary of a set of records
consists of the number and a fixed size digest of records in the
set. See the triplets returned by the Get_Interval_Hashes function in the
bxtree module.
Up: Publication homepage
Peter N. Yianilos
2003-10-10
![]() time. The top level is a communication protocol that directs
the synchronization process so that minimization of bits
communicated, rounds of communication, and local computation
are simultaneously addressed.
time. The top level is a communication protocol that directs
the synchronization process so that minimization of bits
communicated, rounds of communication, and local computation
are simultaneously addressed.





