A Prototype Implementation of
Archival Intermemory

Yuan Chen, Jan Edler, Andrew Goldberg, Allan Gottlieb,
Sumeet Sobti, and Peter Yianilos¹

August 1999

Abstract:

An Archival Intermemory solves the problem of highly survivable digital data storage in the spirit of the Internet. In this paper we describe a prototype implementation of Intermemory, including an overall system architecture and implementations of key system components. The result is a working Intermemory that tolerates up to 17 simultaneous node failures, and includes a Web gateway for browser-based access to data. Our work demonstrates the basic feasibility of Intermemory and represents significant progress towards a deployable system.

Keywords: Archival Storage, Distributed Redundant Databases, Electronic Publishing, Distributed Algorithms, Self-maintenance, Erasure-Resilient Codes, Information, Digital Libraries, Internet.

Introduction

Archival publishing is a crucial aspect of our civilization. Electronic media improves transmission of and access to information, but the important issue of its preservation has yet to be effectively addressed.

The importance of this issue is now apparent as the general objective of preservation has received considerable recent attention [6,11,2,9,7,14,10,13]. In addition, other projects such as [3] appear to be at a formative stage. The notion of Archival Intermemory was introduced in [8].

The Intermemory project aims to develop large-scale highly survivable and available storage systems made up of widely distributed processors that are individually unreliable or untrustworthy--with the overall system nevertheless secure. Inspired by the Internet and Web, but cognizant of the scope of Byzantine threats to any public distributed system, this project further targets self-organization, self-maintenance, and effective administration in the absence of central control.

Intermemory targets a much higher level of fault tolerance than other current approaches. A simple mirror system that maintains 5 copies of the data can tolerate the loss of 4 processors at the expense of multiplying by 5 the total volume of data stored. Through the use of erasure resilient codes [1,12,4], our current design for Intermemory tolerates the loss of any 530 processors with essentially the same factor of 5 space usage. The prototype is smaller and tolerates 17 failures with essentially a factor of 4 in space.²

Another important difference between our project and others is that Intermemory implements a simple block-level storage substrate on which arbitrary data structures may be built--rather than directly storing files or other high-level objects. That is, it performs the role of a disk drive in a conventional nondistributed system. Viewed as a substrate, it frees digital library (and other) system architects from many essential low-level design tasks while not constraining the kind of systems they can build.

This paper reports on a prototype implementation of Intermemory while revising certain aspects of the design given in [8] and giving additional details. The prototype, IM-0, demonstrates:

• The successful cooperation of multiple (over a hundred) subscribers to implement a simple Intermemory. We expect this limit to soon exceed a thousand as we incorporate more hosts and tune the system.

• High availability: data can still be read even if up to 17 subscribers fail.

• A general purpose distributed database synchronization mechanism used for:
  • Automatic dispersal of information throughout the network

  • Self-repair: damaged or lost data is automatically replaced through a subscriber's interactions with its neighbors in the system.

    As a side effect in the context of digital libraries, this solves the media conversion problem. That is, when a failed system is replaced with a new one that may be based on a new hardware storage medium, the contents of its local memory are automatically rebuilt in the new medium. Of course, i) it only solves the problem for information that has already been converted from its original form into Intermemory blocks, and ii) the system we have described does not address preservation of a memory/document's semantics (see section 6 for additional remarks).

• A gateway to the Web that allows one to mount an ISO-9660 CD-ROM image from the Intermemory and access it with a browser.

Each subscriber runs a daemon process. In principle these might be on machines located anywhere in the world, but in this early prototype they are run within a local area network in our laboratory. It is a proof of concept implementation that to some extent addresses all functional features of Intermemory in a less hostile environment, closer to fail-stop than Byzantine.

The strategy of layering has been effective, and perhaps essential, in the development of other highly complex computer systems. Our aim as computer scientists is to create a new low-level layer, a highly durable medium for digital publication. This layer is part of several contexts, most generally that of distributed file systems and databases, but also electronic publishing, and the specific context that provided our original motivation, that of archival preservation of digital information.

Considerable attention in the literature has been devoted to the issue of preservation. The report of the task force on archiving of digital information [7] is an impressive and thoughtful presentation of general issues along with a particular vision for a framework-level solution. In the remainder of the introduction we briefly discuss Intermemory from the perspective of the task force's framework. The rest of this paper describes an early prototype that implements only a portion of our overall design for Intermemory. So our discussion will necessarily involve references to work in progress towards a complete system.

The report envisions a national system of archives, i.e. repositories of digital information. The archiving function is viewed as distinct from that of a digital library.

In contrast, Intermemory aims to preserve the library's contents while serving as a substrate upon which digital library services can be built and provided. Also, we view Intermemory and any resulting library and archive as an international resource--observing that the wide distribution of data increases survivability. We remark, however, that a system of national (or corporate) repositories independent of any digital library service might be implemented using a private access-restricted Intermemory.

Such a national system may prove necessary for legal reasons pointed out in the report. One example is the granting of legal authority to ``rescue'' culturally significant digital information. The report concludes that each repository must be held to a very high standard of survivability. We suggest that a benefit of implementing such repositories using Intermemory is that this standard can be much lower due to the large-scale redundancy inherent in our design.

The report advocates ``migration'' as a key part of the task force's framework solution. They define this as ``the periodic transfer of digital materials from one hardware/software configuration to another, or from one generation of computer technology to a subsequent generation.'' For example, the information contained in database records stored in one format today may be extracted and stored anew using a subsequent database management system.

Migration is contrasted with ``refreshing'' (copying from medium to medium) and ``emulation'' (programming one computing system to closely mimic another). They assert that neither ``sufficiently describes the full range of options needed and available for digital preservation.''

We remark that it is apparent that migration is a complex undertaking, and we are concerned that it may introduce errors that accumulate over time.

From the perspective of the task force's report our approach can be viewed as automated refreshing, with future work towards a single succinctly specified universal low-level emulation environment layer.

The report refers to the computational environment required to interpret an object as its context. Some contexts seem inherently problematic for any approach. Consider, for example, a digital object consisting of a computer game, which depends in a critical way on its host processor's rate of execution, and on the detailed behavior of physical interfaces such as joysticks, game gloves, etc.

Our approach aims to provide long-term access to all materials that have straightforward contexts, and might then serve as the core of an archiving strategy. In this scenario migration is reserved for critical and unusual objects. By focusing migration efforts on fewer digital objects, we suggest that a larger amount of digital information will be to some extent preserved.

Further discussion of the planned emulation component of our Intermemory architecture is beyond the scope of this paper and will be described in a later work.

The report also discusses ``provenance'', which in the context of archival science is described as referring to the ability to prove the ``chain of custody'' of an object tracing back to its source. This is part of the overall task of maintaining the object's integrity.

We remark that our work in progress towards a security infrastructure for Intermemory directly addresses this issue using cryptographic authentication techniques. These allow system data and metadata to be traced back to an originator whose credentials are also ``provable'' within the system.³

To close our discussion of the task force's report we turn to the ``appraisal and selection'' functions of a traditional library or archive, wherein objects are evaluated and selected for inclusion in a collection.

A distributed community of library professionals might continue to apply these functions to create a carefully regulated Intermemory, but other Intermemories may operate with different versions of, or even absent these functions. Because perfect appraisal and selection is impossible without foreknowledge, we suggest that these public Intermemories are complementary and may lead to the preservation of key items that would otherwise be lost.

In section 2 we describe the capabilities of our prototype and the simplifying assumptions made in implementing it. Section 3 presents many aspects of the prototype's internal design, and section 4 describes the Web gateway. Finally, an overview of our project's status and future direction is given in section 6.

Prototype Capabilities

The IM-0 prototype contains two executables. The first is the Intermemory daemon itself, and the second is a control program that, although not required, is commonly used in our development and demonstration environment to start and kill daemons, and to collect error and status messages from them. The following functions are implemented:

• Start a daemon on a specified processor.

• Write a block to an Intermemory address. The system's 64K byte blocks are numbered sequentially from zero. The erasure resilient coded full block is stored at one processor, and 32 fragments are dispersed to other processors. The encoding is such that any 16 of the 32 fragments are sufficient for reconstruction.

• Read a block from an Intermemory address. If the processor storing the full block is unavailable, the system automatically performs a deep read, i.e., obtains 16 dispersed fragments and transparently reconstructs the block.

• Kill an Intermemory daemon. This also deletes its locally stored data.

• Start a replacement daemon.

Subscription is performed offline before the system is started. Also, the security and distributed administration components of the complete system are not present in the prototype, but it is suitable for use in an internal network, such as our lab's. Additional simplifying assumptions relate to the timing of writes and processor deaths: Our demonstrations perform all writes as part of system initialization, after all daemons are started. We assume no processor failures occur during this period. Processor deaths are detected manually, and a replacement daemon is started using the control program.

Distinct from the core IM-0 prototype are utilities we wrote that allow an arbitrary file to be copied into Intermemory and then mounted under Linux as a file system. The same Linux system runs an HTTPD daemon so that any browser connecting to it can retrieve documents stored in this Intermemory-based file system. This is an example of an application built on top of the Intermemory substrate.

A design goal for the Intermemory daemon is that it should consume on average a small portion of its host system's resources--allowing users to contemplate running it on their personal workstation. The prototype achieves this goal and as a result we are able to run many instances of the daemon on a single computer system. On a dual processor 400MHz Pentium II system we have routinely run 20 daemons with little perceptible impact on the system and believe that a much higher loading will prove possible with appropriate system tuning and configuration.

In a simple demonstration of the prototype's capabilities we start 100 daemons (20 on each of 5 hosts), write a block, observe (via the control program's condition reporting facility) the dispersal of fragments throughout the system, and then read the block. Then, the daemon holding the full block is killed and the block is read again. This time, execution is slower because of the overhead of reconstruction.

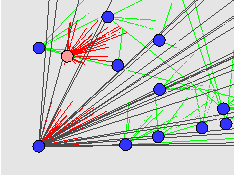
The demonstration we have prepared for the conference starts 13 daemons on each of 8 hosts with a ninth host running the control program and a simulated user process. A graphical output is shown in Figure 1. A number of blocks are then written and the daemons automatically disperse the fragments. Random blocks are now read. While these reads are occurring, five daemons are killed, which causes deeps reads to occur. To demonstrate self repair we enter a cycle where one dead dead daemon is restarted with an empty database and an live daemon is killed. The restarted daemons refill their database during subsequent polls and no longer cause deep reads.

Another possible demonstration initializes the system with a multiblock file. It then kills 17 random daemons, starts replacements, waits long enough so that their contents have been restored, and then repeats the process killing a new randomly chosen set of 17 daemons. Finally, the multiblock file is read to confirm that its contents have not changed.

Consider a similar test that kills 20% of the daemons in each round. When the number of daemons exceeds $90$ (so that 20% is above 17) some data loss is possible. But the chances that $18$ of the 33 daemons holding the block and its fragments are killed is less than $Comb(33,18)\cdot(.2)^{18}$, which is less than $0.05\%$. Given a higher degree dispersal, such as the value of 1024 called for in [8], the situation improves. In this setting the failure probability bound is reduced to $2.6 \times 10^{-55}$.

Finally, we used the mkisofs utility on Linux to create a small ISO-9660 file system (the type found on most CD-ROMs) and using the method mentioned above demonstrate browser access to documents stored in Intermemory.

We do not report performance measurements because it is expected that a complete Intermemory system will exhibit rather different characteristics, so that little would be learned from the exercise.

Prototype Design

Erasure Resilient Codes

Each $64K$ byte data block in our prototype Intermemory is specially encoded as part of the write process. The encoded version is twice the size of the original and is partitioned into 32 fragments of $4K$ bytes. The point of the encoding is that the original data block can be reconstructed (decoded) given any 16 of the fragments.

This basic idea is associated with many names, beginning with Reed-Solomon codes of algebraic coding theory [4]. It was referred to as information dispersal in [12] where the application was similar to ours. It is also associated with the phrase secret sharing in cryptographic contexts, and most recently described as erasure resilient codes⁴ in [1], where highly efficient new algorithms are reported for the encoding and decoding operations.

Our prototype uses an algorithm for encoding and decoding whose time complexity is quadratic in the number of fragments [5].⁵ Linear and nearly linear time algorithms exist, however, and one of these will be substituted in our full implementation. We have performed timings that suggest that, after this substitution, encoding and decoding latency will be dominated by network latency and transmission time.

The $32$ fragments corresponding to a data block are distributed to different daemons. We store the full block in encoded form at a $33$rd processor, which for efficiency's sake is contacted first during a read operation.⁶ If the reader fails to contact this processor, it attempts to contact the other $32$ until $16$ fragments have been collected. Decoding then produces the original data block, transparently satisfying the read request. We refer to the restoration of a block's content from its fragments as a deep read.

Neglecting overhead, the total space consumed in storing a block in our prototype is four times the original: two times for the encoded full block, and another two for all the fragments combined.

For the block to be unreadable, the encoded full block must be unavailable, as must $17$ of its fragments--for a total of $18$ unavailable objects. In this sense the system is 19-fold redundant. Notice that the space required is comparable to the $4$-fold redundancy achieved by deploying $3$ mirror sites.

Our full-scale Intermemory design performs dispersal on a much larger scale as described in [8], achieving 531-fold redundancy while increasing space consumption from four to just five times the original data.

Referring to the $32$-way dispersal of the prototype as level-1 (L1), the full-scale design adds a second level L2. Just as the encoded full block is divided to produce L1 fragments, each L1 fragment is further divided into $32$ smaller L2 fragments giving rise to a $32$-way dispersal tree with $1024$ leaves and the encoded full block at its root.

To understand the rational for this design, consider an alternative where $1024$ fragments are dispersed in a single level. Here, if the full block is unavailable, an additional $512$ network connections are required to read the block. The L1 fragments provide a reasonably efficient backup for the full block since at most 32, and as few as 16 successful connections are required. Moreover, launching this many connections in parallel is reasonable in today's computing environment while $512$ is not.

We have discussed the full design because the prototype's polling loop and database infrastructure, to which we turn next, is fully capable of handling 2-level dispersal. Our prototype is limited to a single level for simplicity and because of the modest scale of our test environment.

Metadata

In addition to maintaining the users' data, the system must maintain various metadata, e.g., the IP addresses of daemons containing dispersed copies of a data block. In the full system the metadata also includes administrative information such as cryptographic credentials for each subscriber.

Most metadata is stored using simple replication. In the prototype every subscriber maintains a complete copy of these metadata records. An approach that scales better with the number of subscribers is given at the end of this section.

The system also contains metadata that exist in only two daemons: A metadata record describing a fragment that has been (or will be) dispersed from daemon A to B is stored on only A and B.

Addressing

Our approach to addressing is an improved (simplified) version of the scheme given in [8].

Each Intermemory block has an $m$-bit Intermemory address $A$. In order to access $A$ we need to determine the Intermemory host storing the encoded full block for $A$. To facilitate replacing failed processors, we split the mapping from addresses to hosts into two parts.

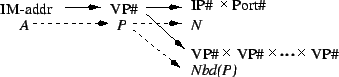
We first map $A$ to a $q$-bit virtual processor number $P$, which is then mapped to a network address $N$ consisting of an IP address $I$ and a port number $S$ (multiple daemons can run on the same node, listening to different ports; each such daemon is a separate virtual processor).

Users need not be Intermemory subscribers to read it and may direct their read request to any functioning daemon in the system.

If a daemon fails and is replaced (e.g., after a host computer crashes or resigns from the Intermemory), we need only change one entry in the $P$ to $N$ mapping, and all Intermemory addresses previously mapped to the dead daemon are now assigned to its replacement.

We also define a mapping from $P$ to the set of virtual processors that form the neighborhood of $P$, and a mapping from $A$ to the set of virtual processors forming the dispersal tree of $A$. The neighborhood is a key idea in our architecture. The mappings that define dispersal trees are constrained so that they embed in the neighborhood graph. That is, if node $x$ is a child of $y$ in the tree, then $x$ is a neighbor of $y$ in the graph. Note that the neighborhood relation is neither symmetric nor reflexive.

In our implementation, $m=128$ and $q=64$. Because of the simplifying assumption in our prototype that all subscriptions are performed offline, the mapping from $A$ to $P$ and the mapping from $P$ to $nbd(P)$ do not change during execution, and hence are hard-coded into the Intermemory daemon. We do support daemon death and replacement so the $P \rightarrow N$ mapping (and other mappings described below) are dynamic metadata. These mappings are stored in a database. Mapping changes are propagated throughout the system by the database synchronization mechanism described below.

In our complete design addresses are assigned as a special case of a single general-purpose distributed administration facility. In the prototype they are preassigned.

Polling Loop

Writing complex concurrent programs is difficult. Our use of database synchronization and a neighborhood polling loop reduces programming complexity and leads to an implementation based on a small number of powerful primitives.

A processor has $32$ neighbors in IM-0. Because of the embedding property mentioned above a processor disperses fragments only to its neighbors, so the dispersal degree is a lower bound on the neighborhood size. The neighbors are assigned pseudorandomly, so the neighborhood graph induced by the arcs from processors to their neighbors is (with extremely high probability) an expander. In particular, the neighborhood graph (almost surely) has a small diameter.

Each subscriber repeatedly executes a polling loop contacting its neighbors one at a time to exchange information with them. Fragment dispersal, metadata propagation, and other tasks are performed during these contacts. In addition to spreading newly added data or metadata throughout the Intermemory, it is the polling loop that enables the system to ``fill'' the local memory of a new daemon that is replacing an old one--or to ``refill'' the local memory of a subscriber whose local database has been lost due to a disk crash or other problem.

It may not be possible to contact every neighbor during a given execution of the polling loop. IM-0 detects unresponsive processors, but takes no special action when this occurs. The complete system design includes a ``death detection'' algorithm that is a special case of the security infrastructure now under construction.

An important role of neighborhoods in the system is to reduce the number of conversations required to perform this information propagation--allowing the system to scale in principle to millions of subscribers. The point is that small neighborhoods combined with the embedding of dispersal trees in the neighborhood graph allow a system to confirm through its polling loop that it holds all needed data--and do so with a relatively small number of network connections.

An Intermemory design objective is that the daemon should use a small fraction of its host system's resources so that it does not significantly impact the host's other computing tasks. A simple amortization strategy to achieve this objective is to introduce a delay after each exchange proportional to the amount of resources consumed. We note, however, the necessity of ensuring that a complete cycle through the polling loop happens rapidly enough so that the resulting rate of system self-repair exceeds the rate at which new errors arise. Under reasonable assumptions in today's environment, this is not a significant constraint. Finally we remark that systems dedicated to Intermemory can easily dispense with this amortization to maximize system performance.

We have found that the combination of a polling loop, random neighborhood structure, and database synchronization (to be described shortly) provides a simple and effective solution to Intermemory self-maintenance and suggest that this approach can be effective for other distributed systems as well.

The Database

An Intermemory daemon's state consists of both data and metadata. The state is stored locally in a database consisting of records of the form (key,version,data,hash). The data field is a function of the key and integral version.⁷ The hash is a digest⁸ of the key, version, and data fields and is used to verify record integrity and by our database synchronization algorithm described later.

Conceptually, the prototype includes six databases (a complete Intermemory system will require several more): The first two hold the system's data, i.e., the encoded blocks and fragments. The next one captures the mapping from block addresses to virtual processors. (The mapping from fragments to virtual processors is determined algorithmically from the previous mapping and the neighborhood mapping, and hence is not tabulated. We do this to avoid the considerable space complexity of explicitly storing the mapping from fragments to virtual processors.) The next two databases contain the mappings from a virtual processors to its network address, and from a virtual processor to its neighbors. The final database contains metadata replicated on only two hosts: It records each processor's accounting of which fragments it will distribute (or has distributed) to its neighbors, as well as which fragments it will receive (or has received). In more detail, the six databases are:

1. Full Blocks: The key is the IM-address, the data is the value of the encoded full block at that address, providing the block has been written.

2. L1 fragments: Recall that an encoded full block is partitioned into $32$ $4$KB L1-fragments. The key is a pair (IM-address, frag_num), where $0 <= frag\_num < 32$; the data is the $4$KB L1-fragment.

3. VP# of Block: The key is an IM-address, the data is the number of the virtual processor containing the encoded full block with this address.

4. Network Address: The key is a virtual processor number; the data is its network address, a pair (IP number, port number).

5. Neighborhood: The key is a virtual processor number; the data is its neighborhood, an ordered list of the virtual processor numbers of its neighbors.

6. L1 Dispersal: The key for this database is more complicated; it is a quadruple (A, B, IM-address, frag_num) and indicates that virtual processor $A$ contains the full block with the given IM-address and disperses the specified L1 fragment to virtual processor $B$. The data is the hash of the L1 fragment in question. Note that the hash is much smaller than the fragment itself (16 bytes verses $4$KB).

We regard these six conceptual databases as one database with records of six types. This is implemented by prepending 2-character designators for each type to the keys described above. Hence each of the original databases appears contiguously when the unified database is viewed in key order. We summarize the IM-0 database (including the two databases not actually stored in the prototype, see below) in Table 1.

Table: IM-0 Database. All entries have VERSION and HASH fields as well.

NAME	KEY		DATA
	type	rest
Full Blocks	FB	IM-addr	$128$KB encoded block
L1 Fragments	L1	(IM-addr, frag_num)	$4$KB L1 fragment
VP# of Block	VP	IM-addr	VP# containing the block
Network Address	NA	VP#	(IP#, port#)
Neighborhood	NB	VP#	VP#s of neighbors
L1 Dispersal	D1	(A,B,IM-addr,frag_num)	hash of the L1 fragment

Synchronization

We use database range synchronization as the main mechanism for data and metadata propagation, in addition to system repair and administration. Input to the range synchronization operation consists of two databases, $A$ and $B$, and a key range $[\ell,h]$. The operation produces three sets of items, with each item falling in the specified range. The first set contains all items with keys in $A$ but not in $B$, the second contains all items with keys in $B$ but not in $A$, and the third contains all items with matching keys but different data or versions.

Our pairwise synchronization algorithm functions by both parties answering queries of the form: what is the hash of all records in the interval $[\ell,h]$?

The daemon's database specification includes this interval hash computation as a built-in function. Regarding the database as a balanced tree our design maintains at each node the xor of the MD5 digests of its entire subtree. Because xor is associative this value may be propagated naturally as part of the tree rotations performed as records are added, deleted, and changed. It is then possible to answer any range hash query in $O(\log n)$ time using this enhanced tree structure. Our prototype fully implements the database interface specification of our design but does not yet include an implementation of this efficient tree structure.

Each communication round of the algorithm partitions the range of interest into a fixed number of subintervals and the parties compute the corresponding interval hash information. Discrepancies are then rapidly localized and dealt with by recursive application to the mismatching subinterval. Synchronization then requires $O(t \log n)$ rounds, where $t$ is the combined size of the three discrepancy sets, and $n$ is the size of the database range to be synchronized. Given the efficient tree design above the total computational burden is $O(t \log^2 n)$.

When a processor $A$ polls processor $B$, the two processors apply database range synchronization and then process each item in the three sets according to the item type as we now describe. The initial range specified selects the entirety of one of the logical databases by using the two letter prefix system described above.

Given the simplifying assumptions we have made for IM-0, we restrict our attention to those actions that result from normal processing, from a daemon being temporarily unavailable, and from the death and subsequent replacement of a daemon at a new network address with all its databases empty.

Full Blocks (FB) and Fragments (L1):

These records are partitioned among the processors so there is no synchronization required. However synchronization of D1 items can cause changes to FB and L1 as described below.

Virtual Processor Number (VP) and Neighborhood (NB):

These databases are not stored in the prototype, since the mappings are constant (see above).

Network Address (NA):

If a record is in one daemon's database but not the other's, it is simply copied over. If both daemons have records with identical keys but different version numbers (meaning a daemon has died and restarted at at new network address), the record with higher version number replaces the one with lower version number.

Dispersals (D1):

Recall that in IM-0 with its static assignment of IM-addresses and fragments to VPs, D1 entries are never updated so all version numbers are 1. Consider D1 record (A, B, IM-address, frag_num). Recall that this record specifies that a full block assigned to $A$ has an L1 fragment assigned to $B$. If the record is missing from $B$'s database, the full block in $A$ needs to be dispersed to $B$. $A$ thus selects the fragment and sends it to $B$ along with the D1 record itself--where they become part of $B$'s L1 and D1 databases.

If the $D1$ record is missing from $A$'s database, it must have ``departed'' subsequent to a previous dispersal of this block from $A$ to $B$. The likely causes are a system crash or media failure on A. The entry in $B$ is now copied to $A$. If the full block is not present in $A$, a deep read is done and the block is inserted.

To illustrate the utility of our polling and synchronization approach we remark that when a daemon in our prototype writes a full block into its database, it also creates entries in its D1 database corresponding to the fragments that must be dispersed. The dispersal then happens over time in the ordinary course of polling and synchronization.

The synchronization rules above presume that there is only one correct data value associated with a given key and version. In the controlled environment in which our prototype functions this is not an issue. But it is a central problem in the design of a complete Intermemory and is dealt with as part of our design for distributed and secure Intermemory administration, which is the subject of a forthcoming pair of papers.

Figure 1: One frame from a real-time graphical visualization of the IM-0 Intermemory prototype running on a cluster of workstations. A total of $104$ copies of the Intermemory engine are active, corresponding to simulated subscribers. Up to 17 may fail with all data remaining continuously available. The display provides a visualization of system activity as it takes place. In the live system (or if this paper is viewed in color) colors indicate subscriber states and types of communication. In the conference proceedings colors are rendered with grayscales. Circles represent subscribers and lines represent communication events between them. Light gray (red) circles represent ``dead/offline'' subscribers. The darker (blue) circles represent ``living/online'' subscribers. Light gray (green) lines indicate ordinary polling-loop communications between subscribers. Dark (brown) indicates read or write operations. In this figure the fan-like pattern of emanating from the subscriber at the lower-left, represents a deep-read. That is, a read operation that must reconstruct a block from $16$ of its $32$ dispersed fragments. The residual ``whiskers'' attached to some subscribers leave a record of failed or abnormal communication attempts. Once normal communication has resumed, they disappear.

Space Complexity

We conclude our discussion of the prototype design by considering the issue of space complexity in greater detail.

Earlier we claimed that IM-0 achieves an availability comparable to maintaining 16 replicas while multiplying the space usage by only 4. Moreover, our ultimate design is to have 2-level dispersion with a fanout of 32, which we have claimed gives effective redundancy of 531 at a storage cost of a 5.

These estimates include only the storage of the blocks and fragments themselves, and as such understate the total space requirements of the system. Additional space is required for i) the key, version, and hash fields of each database record, ii) unused space in the B-tree containing the database, iii) metadata records, iv) additional metadata record types that will be needed for a complete implementation, v) additional fields and records associated with the complete system's cryptographic authentication and administration infrastructure.

We have computed a close approximation to the actual space required to store 10,000 64KB records in our prototype with 100 subscribers assuming data blocks are uniformly distributed. The result is 2,596MB or a little less than 4.1 times the size of the original data. This supports our claim that the space overhead is about the same as maintaining 3 replicas of the data.

The more interesting question is that of scalability. The central problem arises from IM-0's replication of most metadata at every processor. Straightforward analysis of our database schema reveals that in addition to the cost of storing data blocks and their associated fragments, there is an additional space cost of $O(ND)$ at each daemon where $N$ denotes the neighborhood size and $D$ the number of daemons in the system. This analysis includes the VP and NB databases that were omitted from the prototype; the latter is the source of the $O(ND)$ term, which dominates all others.

Our solution is to partition the virtual processors into color classes and to assign a color to each metadata record by hashing its key and version fields.

Records of a given color are then only replicated at processors of the same color.

To obtain the value of a metadata record its color is first computed and a subscriber of that color is then contacted. This is facilitated by maintaining an extended neighborhood color map as part of the polling loop. Still, our current complete design includes an $O(D)$ space term but we view this as acceptable since the leading constant is small.

A complete discussion of this design is beyond the scope of the present paper, and is premature since the detailed design of our full intermemory system is still underway.

The Web Gateway

The Intermemory presents to the world an abstraction of an array of blocks, which may be accessed by address for reading and writing. Subject to the constraints of network connectivity and the security model implemented, any user in the world can access blocks of the Intermemory. To complement our initial Intermemory daemon implementation, we have implemented a subroutine interface that provides the array of blocks abstraction to programmers. The block-oriented abstraction gives Intermemory considerable platform independence and simplifies the design of higher level interfaces, such as distributed file systems, built on top.

Our initial exploration of Intermemory file system issues has focused on the archival storage of data in fairly large coherent pieces. It is, for example, easy to copy a standard ISO-9660 file system image, block for block, to a contiguous range of Intermemory block addresses. To take advantage of this straightforward approach, we have also implemented under Linux a preliminary mechanism for mounting such Intermemory-resident file system images.

Our implementation uses the NBD (Network Block Device) driver in the Linux 2.2 kernel. The NBD device driver implements a UNIX block device, suitable for mounting a file system, by translating all read/write requests into messages to a user-level server via a TCP stream. We wrote such a server to translate NBD requests into Intermemory requests. Since the initial Intermemory prototype has write-once semantics, and there is a block size mismatch between the kernel and the Intermemory, our current server completely avoids the complexity of handling writes. Instead, we use a simple utility to copy a filesystem image directly to Intermemory, without going through the NBD driver or server. Subsequently, we specify read-only access when mounting Intermemory file systems.

Mounting is performed automatically by using the Linux autofs facility. Let <addr> denote the hexadecimal Intermemory address of the first block of a file system whose image is stored in Intermemory. Users refer to files by specifying a path of the form /im/<addr>/path.... We configure autofs so that references to anything under the /im/<addr> directory trigger a mount of the corresponding filesystem. Mounting and unmounting happen transparently to the user, who may be running an HTTP web server or any other ordinary UNIX program. We have used this procedure to provide Web browser access to portions of the Intermemory.

Visualizing Prototype Activity

Even at the scale of our IM-0 prototype, it is difficult to monitor the behavior of a distributed system such as Intermemory. For this reason the prototype includes a special logging facility that reports many events to a central monitoring station.

The resulting log file can then be converted to a sequence of graphical display instructions coded in the PostScript language. We use the ghostscript interpreter to provide real-time visualization of system activity. An example as shown in Figure 1.

The resulting monitoring and visualization facilities were an essential part of our implementation process and we plan to improve both facilities in our future work.

Concluding Remarks

Our continuing studies of Intermemory have strengthened our belief that a system of this nature will be increasingly important as ever more information becomes available world-wide. The success of the IM-0 prototype convinces us that Intermemory is feasible for archival write once applications. We expect that far more general Intermemories are possible and are actively pursuing this direction and considering the important issue of archival semantics, while completing the design and algorithms for a general distributed security and administrative infrastructure. To address the important problem of archival semantics we plan to extend the scope of Intermemory to include a succinctly specified virtual machine and environment, aimed at providing a long-lived emulation-based solution.

Bibliography

1

N. Alon and M. Luby.
A linear time erasure-resilient code with nearly optimal recovery.
IEEE Transactions on Information Theory, 42(6):1732-1736, November 1996.

2

R. J. Anderson.
The eternity service.
In Pragocrypt 96, pages 242-252. CTU Publishing, 1996.

3

M. Beck and T. Moore.
The internet2 distributed storage infrastructure project: An architecture for internet content channels.
University of Tennessee, Department of Computer Science, Technical Report, August 1998.

4

E. R. Berlekamp.
Algebraic Coding Theory.
McGraw-Hill, New York, 1968.

5

J. Bloemer, M. Kalfane, M. Karpinski, R. Karp, M. Luby, and D. Zukerman.
An xor-based erasure-resilient coding scheme.
Technical Report ICSI TR-59-048, International Computer Science Insitute, Berkeley, CA, 1995.

6

A. Crespo and H. Garcia-Molina.
Archival storage for digital libraries.
In Proceedings of the third ACM Conference on Digital libraries (DL '98), pages 69-78, 1998.

7

J. Garrett, D. Waters, H. Gladney, P. Andre, H.Besser, N. Elkington, H. Gladney, M. Hedstrom, P. Hirtle, K. Hunter, R. Kelly, D. Kresh, M. Lesk, M. Levering, W. Lougee, C. Lynch, C. Mandel, S. Mooney, A. Okerson, J. Neal, S. Rosenblatt, and S. Weibe.
Preserving digital information: Report of the task force on archiving of digital information.
Technical report, Commission on Preservation and Access and the Research Libraries Group, Washington D.C. and Mountain View, CA, 1996.

8

A. V. Goldberg and P. N. Yianilos.
Towards and archival intermemory.
In Proceedings of the IEEE Internationl Forum on Research and Technology Advances in Digital Libraries, pages 147-156, Santa Barbara CA, April 1998. IEEE, IEEE.

9

B. Kahle.
Preserving the internet.
Scientific American, pages 82-83, March 1997.

10

R. Kahn and R. Wilensky.
A framework for distributed digital object services.
Technical Report tn95-01, Corporation for National Research Initiatives (CNRI), May 1995.

11

D. M. Levy.
Heroic measures: Reflections on the possibility and purpose of digital preservation.
In Proceedings ACM Digital Libraries 98, pages 152-161, 1998.

12

M. O. Rabin.
Efficient dispersal of information for security, load balancing, and fault tolerance.
Journal of the ACM, 36(2):335-348, April 1989.

13

J. Rothenberg.
Ensuring the longevity of digital documents.
Scientific American, pages 42-47, January 1995.

14

B. Schatz and H. Chen.
Building large-scale digital libraries.
Computer, 29(5):22-26, May 1996.

About this document ...

A Prototype Implementation of
Archival Intermemory

This document was generated using the LaTeX2HTML translator Version 2K.1beta (1.47)

Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.

The command line arguments were:
latex2html -split 0 -image_type gif -nonext_page_in_navigation -noprevious_page_in_navigation -up_url ../main.html -up_title 'Publication homepage' -accent_images textrm -numbered_footnotes improto.tex

The translation was initiated by Peter N. Yianilos on 2002-06-25

Footnotes

... Yianilos¹

The authors are listed in alphabetical order. At the time this prototype was designed all authors were with NEC Research Institute, 4 Independence Way, Princeton, NJ 08540. The first author is also affiliated with Georgia Institute of Technology, the third is now with InterTrust Corporation, the fourth is also with New York University, and the fifth with the University of Washington. Direct correspondence to the sixth author at pny@research.nj.nec.com.

... space.²

We describe in section 3.5 the metadata stored that accounts for the word ``essentially''. As described below our systems encodes blocks in a manner that doubles their size. The prototype stores the encoded block twice, once in complete form, and once in 32 pieces. The full design stores the raw block once and the encoded block twice (in 32 and 1024 pieces).

... system.³

Of course one must worry about the long-term strength of any cryptographic system. We are aware of this concern and plan to eventually address it in our scheme.

... codes⁴

Error correcting codes are a related but distinct concept. These codes add specially computed bits to a data block such that the original data can be recovered in the presence of a bounded number of bit errors at unknown locations anywhere in the resulting enlarged block. The original data is recovered so long as the total number of errors is not too large. An erasure resilient code functions similarly but assumes that some set of known bit positions are unknown, i.e., have been erased.

...BKKKLZ95.⁵

We thank Michael Luby for allowing us to adapt his code for use in our system.

... operation.⁶

The particular encoding used by the prototype has the property that the original block is a prefix of the encoded block. As a result no decoding at all is required when reading it. The prototype stores the complete encoded block to avoid reencoding it each time it must disperse a fragment as part of routine system maintenance.

...version.⁷

In our prototype, data blocks are written only once so their version is always $1$. But the version mechanism is used to propagate revised metadata information.

... digest⁸

The prototype uses the well-known MD5 function.