Up: Publication homepage
1
2
68W01, 68W05, 68W40, 68P10
Locally Lifting the Curse of Dimensionality for
Nearest Neighbor Search
Peter N. Yianilos
July 14, 1999 and, in revised form, June 18, 2002.
Netrics Inc., 707 State Road #212, Princeton, NJ 08540
pny@cs.princeton.edu
Nearest neighbor search, kd-tree, curse of dimensionality
Abstract:
Our work gives a positive result for nearest neighbor search
in high dimensions. It establishes that radius-limited search
is, under particular circumstances, free of the
curse of
dimensionality. It further illuminates the nature of the
curse, and may therefore someday contribute to improved general
purpose algorithms for high dimensions and for general metric
spaces.
We consider the problem of nearest neighbor search in
the Euclidean hypercube ![$[-1,+1]^d$](img21.gif) with uniform
distributions, and the additional natural assumption
that the nearest neighbor is located within a constant
fraction
with uniform
distributions, and the additional natural assumption
that the nearest neighbor is located within a constant
fraction  of the maximum interpoint distance in this space,
i.e. within distance
of the maximum interpoint distance in this space,
i.e. within distance 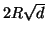 of the query.
of the query.
We introduce the idea of aggressive pruning and
give a family of practical algorithms, an idealized
analysis, and describe experiments. Our main result
is that search complexity measured in terms of
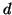 -dimensional inner product operations, is i)
strongly sublinear with respect to the data set size
-dimensional inner product operations, is i)
strongly sublinear with respect to the data set size
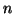 for moderate
for moderate 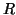 , ii) asymptotically, and as a
practical matter, independent of dimension.
, ii) asymptotically, and as a
practical matter, independent of dimension.
Given a random data set, a random query within
distance 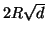 of some database element, and
a randomly constructed data structure, the search
succeeds with a specified probability, which is a
parameter of the search algorithm. On average a
search performs
of some database element, and
a randomly constructed data structure, the search
succeeds with a specified probability, which is a
parameter of the search algorithm. On average a
search performs
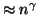 distance computations
where
distance computations
where 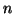 is the number of points in the database,
and
is the number of points in the database,
and 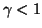 is calculated in our analysis. Linear
and near-linear space structures are described, and
our algorithms and analysis are free of large hidden
constants, i.e. the algorithms perform far less work
than exhaustive search - both in theory and practice.
is calculated in our analysis. Linear
and near-linear space structures are described, and
our algorithms and analysis are free of large hidden
constants, i.e. the algorithms perform far less work
than exhaustive search - both in theory and practice.
2002American Mathematical Society
Finding nearest neighbors in Euclidean spaces of very low
dimension is theoretically fast, and practical, using the
notion of a Voronoi diagram [Aur91]. In
moderate dimension, or in general metric spaces with intrinsically moderate dimension, recursive
projection-decomposition techniques such as kd-trees
[FBS75,FBF77,BF79,Ben80]
and vantage-point techniques
[Uhl91b,Uhl91a,RP92,Yia93]
for general metric spaces of intrinsically low dimension, are
effective.
As dimension 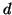 grows large, these tree techniques perform
significantly better than brute-force search only if the
number of dataset points
grows large, these tree techniques perform
significantly better than brute-force search only if the
number of dataset points 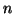 grows exponentially in
grows exponentially in 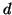 . Or,
in the case of Voronoi diagrams, if space increases
exponentially.
. Or,
in the case of Voronoi diagrams, if space increases
exponentially.
The motivation for this work is the observation that, in
practice, one is usually interested in nearest neighbors only
if they are somewhat close to the query. The main
contribution of this paper is the algorithmic idea of aggressive pruning and its analysis for the uniformly
distributed hypercube. In this setting, with a natural
definition of somewhat close, we show that the expected time
complexity of finding nearest neighbors is invariant with
respect to dimension3 -- and the space cost4 is
independent of 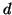 , and linear in
, and linear in 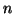 .
.
In a Euclidean hypercube the maximum distance between two
points grows with 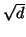 . By somewhat close we mean
within a neighborhood whose radius is a constant fraction
. By somewhat close we mean
within a neighborhood whose radius is a constant fraction 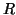 of this distance.
A parameter
of this distance.
A parameter 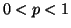 controls the probability that a search
will locate the nearest neighbor within this search domain.
For each choice of
controls the probability that a search
will locate the nearest neighbor within this search domain.
For each choice of 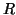 and
and 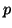 we calculate an exponent
we calculate an exponent 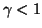 such that the search will perform on average
such that the search will perform on average
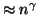 distance computations, and this dominates the work
performed. Notice that
distance computations, and this dominates the work
performed. Notice that 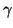 is independent of
is independent of 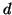 .
.
The practical significance of our work is that search time is
strongly sublinear given moderately large values for 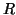 and
acceptable success probabilities. For example, searching
and
acceptable success probabilities. For example, searching
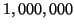 points uniformly distributed in
points uniformly distributed in
![$[-1,+1]^{1000}$](img28.gif) with our experimental software, given
with our experimental software, given 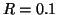 , requires on
average
, requires on
average
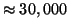 distance computations, and succeeds
with probability
distance computations, and succeeds
with probability 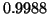 . In this example
. In this example
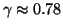 from our analysis. Arbitrarily high success
probabilities can be obtained at the expense of distance
computations.
from our analysis. Arbitrarily high success
probabilities can be obtained at the expense of distance
computations.
We remark that this work was motivated by the author's recent
work of [Yia99], where the objective is to build
a data structure that provides worst-case sublinear-time
radius-limited nearest neighbor search (independent of query)
for a given dataset. With uniform distributions in
Euclidean space, the resulting structures support search
neighborhood of only 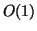 size, in contrast with those of
this paper that scale linearly with the maximum interpoint
distance.
size, in contrast with those of
this paper that scale linearly with the maximum interpoint
distance.
Early work in nearest neighbor search is surveyed in
[Das91].
There is a large literature on the search problem, much
of it elaborating on a single fact: that certain projections
from a metric space to 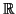 have the property that
projected distances are dominated by those in the original
space.
have the property that
projected distances are dominated by those in the original
space.
The two most important such projections are i) inner product
with a unit vector in Euclidean space, and ii) distance from a
chosen vantage point.5 These ideas were recognized early on in work including
[BK73,Fuk75,Fuk90,FS82,Sha77].
Taking the inner product with a canonical basis element in
Euclidean space leads to the well-known kd-tree of
Friedman and Bentley
[FBS75,FBF77,BF79,Ben80].
They recursively divide a pointset in 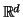 by projecting
each element onto a distinguished coordinate. Improvements,
distribution adaptation, and incremental searches, are
described in [EW82], [KP86], and
[Bro90] respectively.
by projecting
each element onto a distinguished coordinate. Improvements,
distribution adaptation, and incremental searches, are
described in [EW82], [KP86], and
[Bro90] respectively.
The search tree we build has essentially the same structure as
a kd-tree built given randomly pretransformed
data6, and constrained to use the same cut coordinate for all
nodes at a given tree level. Our criterion for pruning
branches during search, and its analysis, are the primary
contributions of this paper and distinguish our methods from
kd-tree search.
More recently, the field of computational geometry has yielded
many interesting results such as those of
[Vai89,Cla88,Cla87,FMT92] and
earlier [DL76].
Very recently a number of papers have appeared striving for
more efficient algorithms with worst-case time bounds for the
approximate nearest neighbor problem
[AMN$^+$94,Kle97,KOR98,IM98]. These exploit
properties of random projections beyond the simple projection distance dominance fact mentioned above, and
additional ideas to establish worst case bounds. Our work may
be viewed as exploiting the fact that random projections of
uniformly random data in a hypercube, and of neighborhood
balls of radius proportional to 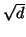 , both have constant
variance with respect to
, both have constant
variance with respect to 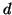 . See also [Cla97] for
very recent work on search in general metric spaces.
. See also [Cla97] for
very recent work on search in general metric spaces.
Several of the papers mentioned above include interesting
theoretical constructions that trade polynomial space, and in
some cases expensive preprocessing, for fast performance in
the worst case. We remark that to be useful in practice, a
nearest neighbor algorithm must require very nearly linear
space -- a stringent requirement. As datasets grow, even
low-degree polynomial space becomes rapidly unacceptable.
For completeness, early work dealing with two special cases
should be mentioned. Retrieval of similar binary keys is
considered by Rivest in [Riv74] and the 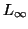 setting is the focus of [Yun76]. Also see
[BM80] for worst case data structures for the range
search problem. Finally, recent works [BOR99] and
[CCGL99] establish nontrivial lower bounds for
nearest neighbor search.
setting is the focus of [Yun76]. Also see
[BM80] for worst case data structures for the range
search problem. Finally, recent works [BOR99] and
[CCGL99] establish nontrivial lower bounds for
nearest neighbor search.
In the following section we give construction and search
algorithms specialized for our uniform setting. Section
3 gives a concrete analysis of these
algorithms that include calculations of the applicable search
time complexity exponent, and failure probability.
Experiments are presented in section 4, which
confirm in practice the dimensional invariance established by
analysis. Finally, some directions for further work are
mentioned in section 5.
Algorithms
A search tree is built with the set of data points as its
leaves. It has essentially the same structure as a kd-tree
built on data that has first been transformed to a random
coordinate system. Construction time is easily seen to be
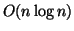 and space is linear.
and space is linear.
Construction proceeds recursively. Each interior node
has as input a list of points. The root's list is the entire
set. Associated with each interior node is a randomly selected
unit vector 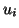 , where
, where 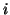 denotes level (distance from the
root). The number of such vectors is then equal to the depth
of tree minus one (because there is no vector associated with
a leaf). This set is constructed so as to be orthonormal.
First, random vectors are drawn, then they are orthonormalized
in the usual way (Gram-Schmidt).
denotes level (distance from the
root). The number of such vectors is then equal to the depth
of tree minus one (because there is no vector associated with
a leaf). This set is constructed so as to be orthonormal.
First, random vectors are drawn, then they are orthonormalized
in the usual way (Gram-Schmidt).
Construction of a node consists of reading its input list,
computing the inner product of each element with the node's
associated 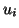 , and adding the element to a left or
right output list depending on its sign. In general the
dividing point is chosen more intelligently, e.g. by
computing the median of the inner product values. But in our
uniform
, and adding the element to a left or
right output list depending on its sign. In general the
dividing point is chosen more intelligently, e.g. by
computing the median of the inner product values. But in our
uniform ![$[-1,+1]^d$](img21.gif) setting we just use zero for simplicity.
Left and right children are then generated recursively. If a
node's input list consists of a single element, then that node
becomes a leaf and stores the element within it.
setting we just use zero for simplicity.
Left and right children are then generated recursively. If a
node's input list consists of a single element, then that node
becomes a leaf and stores the element within it.
The search is parameterized by a query 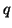 , a value
, a value 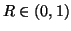 giving the proportional size of the search domain, and
a probability
giving the proportional size of the search domain, and
a probability 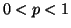 that is related to the success rate we
expect.
that is related to the success rate we
expect.
The inner product of 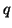 and each
and each 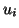 is first computed.
Next the positive threshold distance
is first computed.
Next the positive threshold distance
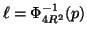 is computed, where
is computed, where 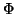 denotes the
cumulative distribution function for a normal density with
the variance indicated by subscript.
denotes the
cumulative distribution function for a normal density with
the variance indicated by subscript.
Search proceeds recursively from the root. For a node at
level 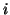 the value
the value 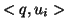 is examined. If it is less than
is examined. If it is less than
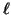 then the left child is recursively explored. If it
exceeds
then the left child is recursively explored. If it
exceeds 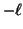 then the right child is explored. Notice that
when
then the right child is explored. Notice that
when
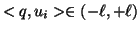 both children are explored.
When a leaf is encountered, the distance is computed between
the element it contains and
both children are explored.
When a leaf is encountered, the distance is computed between
the element it contains and 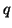 .
.
This decision rule is centered at zero because of our
particular uniform ![$[-1,+1]^d$](img21.gif) setting, but is easily
translated to an arbitrary cut point, e.g. the median of the
projected values.
setting, but is easily
translated to an arbitrary cut point, e.g. the median of the
projected values.
After each distance computation 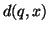 is performed the
proportion
is performed the
proportion
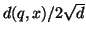 is computed. If smaller than
is computed. If smaller than
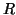 , then
, then 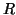 is reduced and
is reduced and 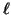 recomputed.
recomputed.
This concludes the description of our search algorithm and
we now briefly discuss related issues and extensions.
An important idea in kd-tree search involves the computation
of the minimum distance from the query to the subspace
corresponding to a node to be explored. If this distance grows beyond
the radius of interest, the node is pruned. We do not,
however, include it in our analysis or experimental
implementation because in our high dimensional setting, in the
absence of exponentially many data elements, this idea has
vanishingly little effect. Intuitively, this is because the
search tree is not nearly deep enough for the minimum distance
to grow larger than the search radius.
The analogue of this kd-tree idea in our setting is an
alternative version of our algorithm above that slightly
reduces 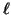 while descending through interior nodes to
reflect the fact that the distribution of data elements within
a ball about the query is no longer uniform. But, again, this
is a second order effect.
while descending through interior nodes to
reflect the fact that the distribution of data elements within
a ball about the query is no longer uniform. But, again, this
is a second order effect.
Finally we remark that the 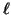 -cutoff approach taken
above might be replaced with an entirely probabilistic pruning
scheme that passes probabilities from our analysis down to
each child during search. The probabilities upward to the
root are then multiplied and search continues downward until
the result falls below a specified threshold.
-cutoff approach taken
above might be replaced with an entirely probabilistic pruning
scheme that passes probabilities from our analysis down to
each child during search. The probabilities upward to the
root are then multiplied and search continues downward until
the result falls below a specified threshold.
Analysis
We assume both data points and queries are uniformly
distributed within the hypercube ![$[-1,+1]^d$](img21.gif) . The Euclidean
distance metric applies and the maximum distance between two
points in this space is
. The Euclidean
distance metric applies and the maximum distance between two
points in this space is 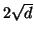 .
We consider the problem of finding the nearest neighbor of a query
.
We consider the problem of finding the nearest neighbor of a query
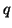 within some distance
within some distance 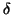 that is a constant proportion
of the maximum interpoint distance, i.e.
that is a constant proportion
of the maximum interpoint distance, i.e.
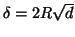 with
with 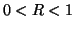 .
.
Any unit vector 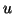 gives rise to a projection
gives rise to a projection 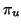 mapping
mapping
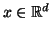 into
into 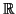 defined by
defined by 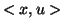 . It is
immediate that distances in the range of this projection are
dominated by distances in the domain. It is this fact that
kd-trees exploit to prune branches during branch-and-bound
search.
. It is
immediate that distances in the range of this projection are
dominated by distances in the domain. It is this fact that
kd-trees exploit to prune branches during branch-and-bound
search.
If 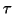 represents the distance to the nearest neighbor
encountered so far during a search, then this fact implies
that every member of the ball of radius
represents the distance to the nearest neighbor
encountered so far during a search, then this fact implies
that every member of the ball of radius 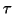 centered at the
query
centered at the
query 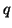 maps under any
maps under any 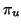 into the interval
into the interval
![$[\pi_u(q)-\tau, \pi_u(q)+\tau]$](img59.gif) . So kd-tree search may
confidently disregard any data points that project outside of
this interval.
Unlike the kd-tree, which finds nearest neighbors with certainty,
we will consider randomized constructions that succeed with
some specified probability.
. So kd-tree search may
confidently disregard any data points that project outside of
this interval.
Unlike the kd-tree, which finds nearest neighbors with certainty,
we will consider randomized constructions that succeed with
some specified probability.
Since 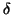 scales up linearly with
scales up linearly with 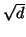 , the interval
grows
, the interval
grows
![$[\pi_u(q)-\delta, \pi_u(q)+\delta]$](img60.gif) too, and soon the
kd-tree can confidently prune almost nothing, and
performs a nearly exhaustive search.
too, and soon the
kd-tree can confidently prune almost nothing, and
performs a nearly exhaustive search.
But in our uniformly random setting we will show that the
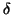 ball about
ball about 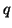 projects to a distribution about
projects to a distribution about
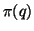 having constant variance. This is why it is possible
to continue to probabilistically prune just as
effectively even as
having constant variance. This is why it is possible
to continue to probabilistically prune just as
effectively even as
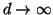 . Since dimension
does not affect our ability to prune, we have lifted the curse
of dimensionality in our setting.
. Since dimension
does not affect our ability to prune, we have lifted the curse
of dimensionality in our setting.
We now proceed with the description and idealized analysis of
our algorithm with the following proposition, which establishes
two elementary but key dimensional invariants
Proposition 3.1
i) Let
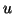
be a random unit vector, and let
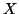
denote a random dataset in our setting, then the one
dimensional set of values
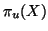
has mean zero and
variance
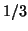
- independent of dimension - where
both
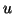
and
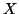
are random variables.
ii) Consider any
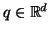
and let
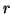
denote a
random vector located on the surface of a ball
centered at
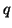
of radius
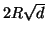
. Then for
any unit vector
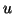
, the distribution of values
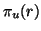
has mean
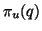
and variance
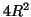
-
independent of dimension.

Now fix some unit vector 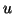 and consider the query's
projection
and consider the query's
projection 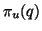 . Then by Proposition 3.1, and
ignoring hypercube corner effects, the projection of the
data points within the domain of search are distributed about
. Then by Proposition 3.1, and
ignoring hypercube corner effects, the projection of the
data points within the domain of search are distributed about
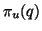 with variance no greater than
with variance no greater than 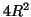 .
.
Because distances between projected points are dominated by
their original distance it is clear that
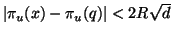 for any
for any 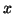 in the search domain.
in the search domain.
So any data points with projections farther than 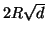 from
from
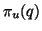 can be confidently ruled out during search. It is
this hard pruning that kd-trees (and many related
structures) exploit to avoid considering every point during
nearest neighbor search.
can be confidently ruled out during search. It is
this hard pruning that kd-trees (and many related
structures) exploit to avoid considering every point during
nearest neighbor search.
But notice that this pruning cutoff distance
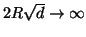 with
with 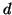 while the projection variance
remains constant. As a result hard pruning is asymptotically
ineffective, and this gives rise to the curse of
dimensionality for nearest neighbor search using kd-trees in
our setting.
while the projection variance
remains constant. As a result hard pruning is asymptotically
ineffective, and this gives rise to the curse of
dimensionality for nearest neighbor search using kd-trees in
our setting.
Next observe that as a consequence of the central limit
theorem the distributions of Proposition 3.1 are
asymptotically normal -- and we remark that as a practical
matter this is a good approximation; even for moderate
dimension. So from this point on in our analysis we will
simply assume normality, i.e. that 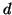 is sufficiently large
so that its deviation from normality is negligible.
is sufficiently large
so that its deviation from normality is negligible.
We then arrive at one of the main observations of this paper:
that the nearest neighbor's projection is within constant
distance of 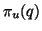 with arbitrarily high and easily
calculated probability
with arbitrarily high and easily
calculated probability 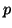 depending only on this constant,
and not on
depending only on this constant,
and not on 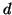 .
.
Recall that the tree we build recursively bisects the set of
data points using a randomly selected 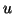 by separating its
projection into left and right branches at a cut point
by separating its
projection into left and right branches at a cut point 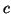 near the median. Given a query
near the median. Given a query 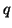 we prune one of these
branches if
we prune one of these
branches if 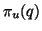 is at least some cutoff distance
is at least some cutoff distance 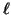 from
from 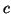 . We refer to this idea as aggressive pruning.
. We refer to this idea as aggressive pruning.
Proposition 3.2
Using cutoff distance
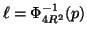
to
prune branches will exclude the nearest neighbor
(assuming one exists within distance
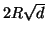
of
the query) with probability
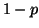
at each node; where
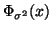
denotes the cumulative
distribution function for the zero mean normal density
with variance
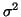
.
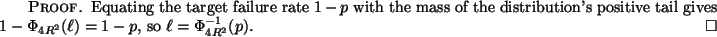
Again, note that this cutoff distance 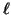 is constant
despite the fact that the absolute size of our search domain
is expanding with
is constant
despite the fact that the absolute size of our search domain
is expanding with 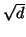 as
as
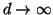 .
We can now establish a single tree's expected search complexity
and success probability.
.
We can now establish a single tree's expected search complexity
and success probability.
Proposition 3.3
Given
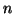
data points,
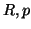
, and
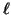
from
proposition
3.2, and assuming
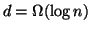
, then i) our search will visit
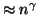
leaf nodes where
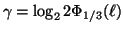
, and
compute a
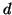
-dimensional Euclidean distance at
at each; and ii) the search will succeed
with probability no smaller than
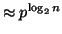
.

Notice that the exponent of 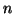 in proposition 3.3
is within
in proposition 3.3
is within 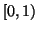 . Also, the requirement that
. Also, the requirement that
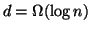 is not very restrictive since otherwise the number
of data points is exponential in
is not very restrictive since otherwise the number
of data points is exponential in 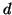 and earlier techniques
can be used to efficiently locate nearest neighbors.
and earlier techniques
can be used to efficiently locate nearest neighbors.
The probability estimate of Proposition 3.3 is
extremely conservative. The actual failure
probabilities are much smaller because: i) our analysis has
implicitly assumed that the query always projects to a point
exactly 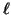 from the cut point. This is the worst case.
If the distance is smaller, then nothing is pruned and no
error can be made; and if the distance is larger, the
effective cutoff distance is effectively increased; and ii) we
have assumed that the nearest neighbor is always just within
the domain of search. In reality queries will be distributed
with this domain.
from the cut point. This is the worst case.
If the distance is smaller, then nothing is pruned and no
error can be made; and if the distance is larger, the
effective cutoff distance is effectively increased; and ii) we
have assumed that the nearest neighbor is always just within
the domain of search. In reality queries will be distributed
with this domain.
Table 1:
Searches in our setting with a single tree require
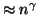 inner product operations and linear space. This
table gives
inner product operations and linear space. This
table gives 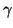 values for various choices of
values for various choices of 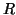 and
and 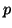 from
our analysis.
from
our analysis.
| R |
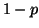 |
| |
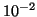 |
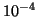 |
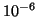 |
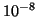 |
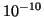 |
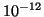 |
| 0.01 |
0.090 |
0.141 |
0.177 |
0.207 |
0.232 |
0.254 |
| 0.02 |
0.174 |
0.267 |
0.331 |
0.381 |
0.423 |
0.458 |
| 0.03 |
0.252 |
0.379 |
0.463 |
0.526 |
0.577 |
0.618 |
| 0.04 |
0.325 |
0.479 |
0.575 |
0.645 |
0.698 |
0.740 |
| 0.05 |
0.393 |
0.566 |
0.669 |
0.739 |
0.790 |
0.829 |
| 0.06 |
0.456 |
0.642 |
0.746 |
0.813 |
0.859 |
0.892 |
| 0.07 |
0.513 |
0.707 |
0.808 |
0.869 |
0.908 |
0.935 |
| 0.08 |
0.566 |
0.763 |
0.858 |
0.911 |
0.943 |
0.963 |
| 0.09 |
0.615 |
0.810 |
0.897 |
0.941 |
0.965 |
0.979 |
| 0.10 |
0.660 |
0.850 |
0.926 |
0.962 |
0.980 |
0.989 |
| 0.11 |
0.700 |
0.882 |
0.949 |
0.976 |
0.989 |
0.995 |
| 0.12 |
0.737 |
0.909 |
0.965 |
0.986 |
0.994 |
0.998 |
| 0.13 |
0.770 |
0.931 |
0.977 |
0.992 |
0.997 |
0.999 |
| 0.14 |
0.800 |
0.948 |
0.985 |
0.995 |
0.999 |
1.000 |
| 0.15 |
0.826 |
0.961 |
0.990 |
0.997 |
0.999 |
1.000 |
| 0.16 |
0.850 |
0.971 |
0.994 |
0.999 |
1.000 |
1.000 |
| 0.17 |
0.871 |
0.979 |
0.996 |
0.999 |
1.000 |
1.000 |
| 0.18 |
0.890 |
0.985 |
0.998 |
1.000 |
1.000 |
1.000 |
| 0.19 |
0.906 |
0.990 |
0.999 |
1.000 |
1.000 |
1.000 |
| 0.20 |
0.921 |
0.993 |
0.999 |
1.000 |
1.000 |
1.000 |
|
Even without considering these factors our calculations
suggest that efficient search is possible for moderately
large values of 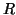 .
.
Table 3 gives exponent values for selected
values of 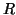 and
and 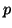 . For example, if
. For example, if 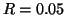 and
and
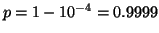 then the exponent is
then the exponent is 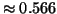 .
Given
.
Given
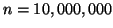 data points our results state that no
more than
data points our results state that no
more than
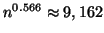 inner product operations
will be performed, and that the nearest neighbor will be
located with probability
inner product operations
will be performed, and that the nearest neighbor will be
located with probability
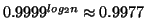 .
Choosing
.
Choosing
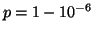 corresponds to
corresponds to 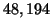 inner
products with the probability of success increasing to
inner
products with the probability of success increasing to
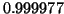 . All of these calculations are asymptotically
independent of dimension.
. All of these calculations are asymptotically
independent of dimension.
We continue this example to illustrate the use of forests to
improve performance in some settings. Later we will give a
theoretical consequence of this idea. Consider two
independent trees with
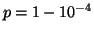 . That is, the choice
of random unit vectors is independent. Both trees are
searched for each query. We then expect a failure rate of
. That is, the choice
of random unit vectors is independent. Both trees are
searched for each query. We then expect a failure rate of
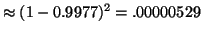 , and
, and
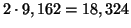 inner products are performed.8 Now this failure
rate is considerably better than the
inner products are performed.8 Now this failure
rate is considerably better than the
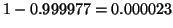 resulting from a single tree using
resulting from a single tree using
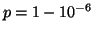 , and far
fewer inner products are computed, but space consumption is
doubled. This example illustrates the space-time design
tradeoff that arises when applying our ideas in practice.
, and far
fewer inner products are computed, but space consumption is
doubled. This example illustrates the space-time design
tradeoff that arises when applying our ideas in practice.
The natural generalization of this idea leads to a forest of
independent trees. Recall that a failure rate of a single
tree grows, albeit slowly, with 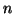 . By using enough trees
one can force the forest's failure rate to zero as
. By using enough trees
one can force the forest's failure rate to zero as 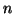 increases while preserving sublinear search times; at the
expense of polynomial space to pay for the additional trees.
To analyze this let
increases while preserving sublinear search times; at the
expense of polynomial space to pay for the additional trees.
To analyze this let 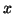 denote the tree's depth and observe
that
denote the tree's depth and observe
that 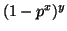 gives the probability of failure for a forest
of
gives the probability of failure for a forest
of 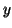 distinct random trees. It can be shown that if
distinct random trees. It can be shown that if
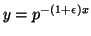 for any
for any 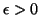 , then this
probability tends to zero as
, then this
probability tends to zero as 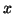 (and therefore
(and therefore 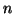 )
increases9. Since
)
increases9. Since 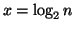 the number of
trees
the number of
trees
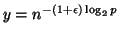 in terms of
in terms of 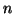 .
Search time (the number of inner product operations) also
increases by a factor of
.
Search time (the number of inner product operations) also
increases by a factor of 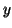 . Space increases from linear to
. Space increases from linear to
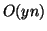 . Finally, to maintain independence we must increase
the lower bound on
. Finally, to maintain independence we must increase
the lower bound on 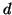 to
to
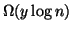 .
.
It is apparent from table 3 that this idea works
for many values of R and p. For example, if 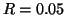 and
and
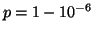 then the original exponent
then the original exponent 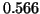 increases by
only
increases by
only
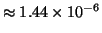 - far less than the
table's precision. But it does not work for arbitrary
- far less than the
table's precision. But it does not work for arbitrary 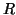 and
and
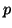 . For large values of
. For large values of 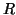 the exponent is so close to
the exponent is so close to 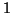 that the added complexity makes the total superlinear.
that the added complexity makes the total superlinear.
Note that 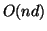 space is required to store the data elements
themselves, but only
space is required to store the data elements
themselves, but only 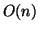 space is needed for the interior
tree nodes, which point to data elements. So, in practice, we
can afford
space is needed for the interior
tree nodes, which point to data elements. So, in practice, we
can afford 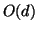 trees while remaining linear space. In
practice this means that in high dimension one can easily
afford many trees without materially affecting space
consumption. In theory it means that if
trees while remaining linear space. In
practice this means that in high dimension one can easily
afford many trees without materially affecting space
consumption. In theory it means that if 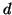 is assumed to
grow as an appropriate small power of
is assumed to
grow as an appropriate small power of 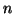 as
as
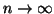 , then the entire forest occupies linear space.
, then the entire forest occupies linear space.
Returning to our choice of the ![$[-1,+1]^d$](img21.gif) hypercube, we observe
that i) All of our arguments apply immediately to
hypercube, we observe
that i) All of our arguments apply immediately to ![$[0,1]^d$](img121.gif) after compensating for the shifted mean, and ii) that our
arguments apply as well to the
after compensating for the shifted mean, and ii) that our
arguments apply as well to the 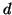 -dimensional hypersphere.
To see this note that the dot product of a random unit vector
and a random database element has variance
-dimensional hypersphere.
To see this note that the dot product of a random unit vector
and a random database element has variance 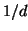 , and the maximum
interpoint distance is constant, so the projection of a
proportional neighborhood balls also falls with
, and the maximum
interpoint distance is constant, so the projection of a
proportional neighborhood balls also falls with 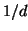 .
.
Finally we remark that as an alternative to forests, one can
build a single tree in which each level is overlapped,
i.e. items near the center are stored in both the left and
right branches. This effectively reduces 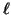 and with it
search time - at the expense of polynomial space (given a
constant fraction of overlap at each level).
and with it
search time - at the expense of polynomial space (given a
constant fraction of overlap at each level).
Experiments
To confirm our analysis we wrote an ANSI-C program to build
and search trees. It accepts 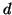 ,
, 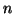 ,
, 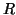 ,
, 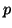 as arguments,
in addition to the number of random queries to test, and a
random seed.
as arguments,
in addition to the number of random queries to test, and a
random seed.
The data points are distributed uniformly in ![$[-1,+1]^d$](img21.gif) .
Queries are generated by choosing a data point
.
Queries are generated by choosing a data point 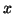 at random,
then a random unit vector
at random,
then a random unit vector 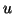 , and forming the sum
, and forming the sum
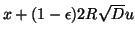 - so that the query lies just
inside of the search domain. We use
- so that the query lies just
inside of the search domain. We use
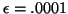 . This
ensures that a nearest neighbor exists within the domain.
. This
ensures that a nearest neighbor exists within the domain.
An indexed set of projection vectors is generated by starting
with random vectors and orthonormalizing them in the standard
way. Each level in the tree uses the corresponding vector in
this set as its projector. So the size of the set is
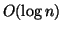 , and in practice is
, and in practice is
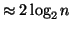 because
the resulting trees are not perfectly balanced. For
simplicity zero is always used as the cut point during tree
construction.
because
the resulting trees are not perfectly balanced. For
simplicity zero is always used as the cut point during tree
construction.
In order to allow us to simultaneously explore large 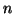 and
and
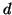 without exceeding available RAM, we represent the data
points to be searched using a pseudorandom generator seed that
suffices to construct them. As a result we can easily study
without exceeding available RAM, we represent the data
points to be searched using a pseudorandom generator seed that
suffices to construct them. As a result we can easily study
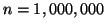 and higher in almost arbitrarily high
dimension.
and higher in almost arbitrarily high
dimension.
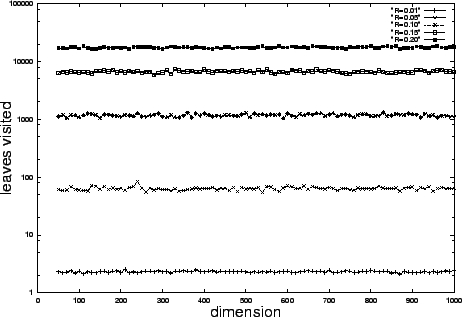
Figure 1 illustrates that search complexity measured
in the number of inner product operations performed is very
nearly dimension-invariant -- confirming our analysis.
So total work scales up only linearly with dimension with
the complexity of an inner product operation.
Note that for simplicity we regard an inner product operation
and a Euclidean distance computation as having identical
complexity. Also, the table's results exclude the roughly 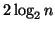 inner products required to compute the query's
projection at each level of the tree.
inner products required to compute the query's
projection at each level of the tree.
Figure 1:
Proportional radius search complexity is constant with respect to
dimension -- confirming our analysis. We measure the
number of leaves visited. Each visit corresponds to a
Euclidean distance computation.
In this experiment the number of uniformly distributed
data points 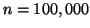 , and the
, and the 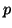 from our
analysis is
from our
analysis is 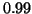 .
Each query is generated so as to be slightly less
than distance
.
Each query is generated so as to be slightly less
than distance 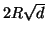 from some database element,
so that our radius-limited search always succeeds.
The results of
from some database element,
so that our radius-limited search always succeeds.
The results of 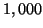 such random
queries are averaged to produce each data point.
Our analysis predicts constant values of approximately
such random
queries are averaged to produce each data point.
Our analysis predicts constant values of approximately
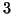 ,
, 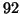 ,
, 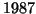 ,
, 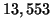 , and
, and 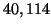 corresponding to
corresponding to 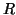 values of
values of
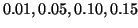 , and
, and 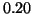 respectively. The experimental
values compare well with these estimates, and in general are
dominated by them by a factor of approximately two.
respectively. The experimental
values compare well with these estimates, and in general are
dominated by them by a factor of approximately two.
|
Recall that our analysis of failure rate was quite
conservative and experiments confirm this. Actual failure
rates for every case in Figure 1 were somewhat
lower than those from analysis. For example, in the 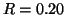 case, analysis predicts that the search will succeed with
probability
case, analysis predicts that the search will succeed with
probability 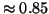 , and the actual value is
, and the actual value is 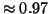 . Note that one reason for using the moderate value
. Note that one reason for using the moderate value
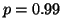 in our study is that we have confirmed that values
far closer to zero result in no observable experimental error
given the limited number of queries we have time to perform.
in our study is that we have confirmed that values
far closer to zero result in no observable experimental error
given the limited number of queries we have time to perform.
We compare performance in our setting with kd-tree search
[FBS75,FBF77,BF79,Ben80].
We are interested in neighbors within a specified distance of
the query. To reproduce this setting, kd-tree search is
initialized as though an element at the specified distance has
already been encountered.
A recent kd-tree implementation [MA99] is modified for
our experiments. Its core routines are altered to support
radius-limited search as described above, and the
distribution's sample program is adapted to report the average
number of distance computations performed in response to each
query. As in our earlier experiments, queries are generated
by starting at a database element, and moving the specified
distance away in a random direction. So every query in our
experiment locates a nearest neighbor within the radius of
interest. As a self-check the sample program is further
modified to verify this condition. After these modifications,
a direct comparison is possible between our method and kd-tree
search.
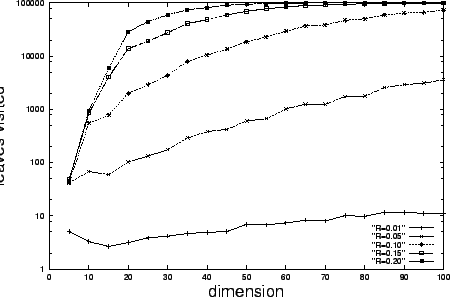
From our analysis it is clear that kd-tree search will not
exhibit the same dimensional invariance, and figure 2
confirms this.
Moreover, search time grows so rapidly for the
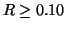 cases that the tree is essentially ineffective by
dimension
cases that the tree is essentially ineffective by
dimension 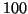 . By contrast (figure 1) our method
remains effective for arbitrarily high dimension. Recall,
however, that kd-tree search is guaranteed to find the nearest
neighbor within in the domain, while our method will fail with
some small probability.
. By contrast (figure 1) our method
remains effective for arbitrarily high dimension. Recall,
however, that kd-tree search is guaranteed to find the nearest
neighbor within in the domain, while our method will fail with
some small probability.
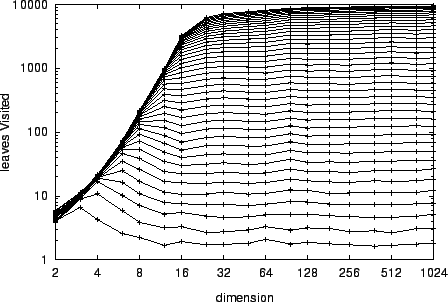
A primary motivation for this paper was our discovery in
[Yia99] that kd-trees, and a related general
structure called a vantage point forest, do exhibit
search complexity that is invariant with respect to dimension
for a domain of constant radius -- and substantial
savings over exhaustive search are realized only for
disappointingly small radii. The experiment reported in
figure 3 confirms this, and illustrates the
fundamentally different asymptotic behavior (with respect to
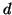 ) of kd-tree search and our aggressive pruning
approach.
The flat graphs of figure 1 are in the presence
of a search radius that grows with
) of kd-tree search and our aggressive pruning
approach.
The flat graphs of figure 1 are in the presence
of a search radius that grows with 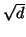 , where those
of 3 assume a search radius that is constant
with respect to
, where those
of 3 assume a search radius that is constant
with respect to 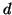 .
For example, by dimension
.
For example, by dimension 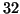 a domain of unity
radius generates a nearly exhaustive search. By contrast
figure 1 shows that for
a domain of unity
radius generates a nearly exhaustive search. By contrast
figure 1 shows that for 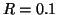 and
and 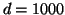 (corresponding to a radius of
(corresponding to a radius of
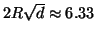 ), our
search visits only roughly
), our
search visits only roughly 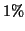 of the leaf nodes.
of the leaf nodes.
Figure 2:
Proportional radius kd-tree search complexity is not
constant with respect to dimension, and increases
rapidly for 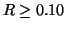 so that by dimension
so that by dimension 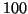 the search is nearly exhaustive. Each node visit
corresponds to a Euclidean distance computation.
The number of uniformly distributed data points
the search is nearly exhaustive. Each node visit
corresponds to a Euclidean distance computation.
The number of uniformly distributed data points 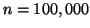 , and the results of
, and the results of 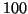 random queries generated
as in figure 1 are averaged to produce each
data point.
random queries generated
as in figure 1 are averaged to produce each
data point.
|
We conclude our discussion of experiments by describing a
single example of our method in greater detail that pushes 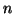 upward to
upward to 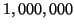 ,
, 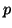 up to
up to 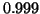 , and the number of
queries up to
, and the number of
queries up to 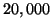 . The dimension is
. The dimension is 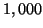 . Here,
analysis predicts success probability
. Here,
analysis predicts success probability 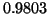 and we observe
and we observe
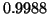 . The tree's depth is
. The tree's depth is 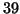 and
and 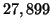 leaves are
visited on average during a search. The predicted value is
leaves are
visited on average during a search. The predicted value is
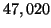 . The experiment required
. The experiment required 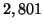 seconds on a 400Mhz
Pentium II processor.
seconds on a 400Mhz
Pentium II processor.
Figure 3:
The average complexity of fixed-radius kd-tree search
is invariant with respect to dimension.
Here 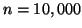 and the graphs from bottom to
top correspond to radii from
and the graphs from bottom to
top correspond to radii from 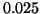 to
to 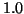 in
increments of
in
increments of 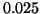 .
.
|
Concluding Remarks
We hopes this work takes us closer to practical and useful
nearest neighbor search in high dimension. In addition to
sharpening our analysis for the uniform case, future
theoretical work might target distribution-independent bounds
for approximate nearest neighbor search within an 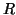 -domain.
While generalizing we expect that the definition of an
-domain.
While generalizing we expect that the definition of an
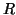 -domain will have to change, and that it may be necessary
to move to the approximate nearest neighbor framework where
the objective is to find neighbors within a
-domain will have to change, and that it may be necessary
to move to the approximate nearest neighbor framework where
the objective is to find neighbors within a 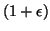 factor of the closest.
factor of the closest.
Also, the work of this paper motivates us to consider
techniques for general metric spaces and arbitrary
distributions that learn the projection distributions
and 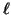 from examples -- adapting to the problem domain.
from examples -- adapting to the problem domain.
Ultimately we envision a high-level procedure that like the
qsort() function from the standard Unix library, views
its underlying database through a layer of abstraction. In
the case of sorting, a comparison function is provided. For
nearest neighbor search projection and distance computation
must be supported.
Sorting is, however, a much simpler problem in as much as
practical algorithms exist with acceptable worst
case time and space complexity -- independent of the dataset.
For nearest neighbor search we suggest that a general tool
must be flexible and
ideally support:
- User supplied distance functions and projectors.
If the projectors are known to be independent
(as in orthogonal Euclidean projections) then
search should exploit this. Most generally a
system might try to learn patterns of
independence from examples.
Special support for discrete-valued distance
functions is also desirable.
- A user specified target success probability,
perhaps requiring the user to provide a
function to generate random queries
for the problem domain.
- A user specified approximation factor
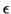 ,
where success is then defined as locating an
element within a factor of
,
where success is then defined as locating an
element within a factor of 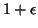 of the
nearest.
of the
nearest.
- A simple bound on the work performed during
search, after which it is simply truncated.
- Control over the time invested in construction to
optimize the resulting data structure.
- Control over the time-space tradeoff. That is, the
ability to invest additional space to improve search
performance.
- Dynamic operation, i.e. the addition and deletion of
points from the data structure during use (not discussed
in this paper -- but clearly possible).
We hope that the ideas and results of this paper brings us closer
to the development of such a tool.
The author thanks Joe Kilian and Warren Smith for helpful discussions.
- AMN$^+$94
-
S. Arya, D. Mount, N. Netanyahu, R. Silverman, and A. Wu, An optimal
algorithm for approximate nearest neighbor searching in fixed dimension,
Proc. 5th ACM-SIAM SODA, 1994, pp. 573-583.
- Aur91
-
Franz Aurenhammer, Voronoi diagrams - a survey of a fundemental
geometric data structure, ACM Computing Surveys 23 (1991), no. 3.
- Ben80
-
Jon Louis Bentley, Multidimensional divide-and-conquer,
Communications of the ACM 23 (1980), no. 4.
- BF79
-
Jon Louis Bentley and Jerome H. Friedman, Data structures for range
searching, Computing Surveys (1979).
- BK73
-
W. A. Burkhard and R. M. Keller, Some approaches to best-match file
searching, Communications of the ACM 16 (1973), no. 4.
- BM80
-
J. L. Bentley and H. A. Maurer, Efficient worstcase data structures for
range searching, Acta Informatica 13 (1980), no. 2, 155-168.
- BOR99
-
Allan Borodin, Rafail Ostrovsky, and Yuval Rabani, Lower bounds for high
dimensional nearest neighbor search and related problems, Proc. 31st ACM
STOC, 1999, pp. 312-321.
- Bro90
-
Alan J. Broder, Strategies for efficient incremental nearest neighbor
search, Pattern Recognition 23 (1990), no. 1/2.
- CCGL99
-
Amit Chakrabarti, Bernard Chazelle, Benjamin Gum, and Alexy Lvov, A lower
bound on the complexity of approximate nearest neighbor searching on the
hamming cube, Proc. 31st ACM STOC, 1999, pp. 305-311.
- Cla87
-
Kenneth L. Clarkson, New applications of random sampling in computational
geometry, Discrete & Computational Geometry 2 (1987), 195-222.
- Cla88
-
Kenneth L. Clarkson, A randomized algorithm for closest-point queries,
SIAM Journal on Computing 17 (1988), no. 4.
- Cla97
-
Kenneth L. Clarkson, Nearest neighbor queries in metric spaces, Proc.
29th ACM STOC, 1997, pp. 609-617.
- Das91
-
Belur V. Dasarathy (ed.), Nearest neighbor pattern classification
techniques, IEEE Computer Society Press, 1991.
- DL76
-
David Dobkin and Richard J. Lipton, Multidimensional searching problems,
SIAM Journal on Computing 5 (1976), no. 2.
- EW82
-
C. M. Eastman and S. F. Weiss, Tree structures for high dimensionality
nearest neighbor searching, Information Systems 7 (1982), no. 2.
- FBF77
-
Jerome H. Friedman, Jon Louis Bentley, and Raphael Ari Finkel, An
algorithm for finding best matches in logarithmic expected time, ACM
Transactions on Mathematical Software 3 (1977), no. 3.
- FBS75
-
Jerome H. Friedman, Forest Baskett, and Leonard J. Shustek, An algorithm
for finding nearest neighbors, IEEE Transactions on Computers (1975).
- FMT92
-
Alan M. Frieze, Gary L. Miller, and Shang-Hua Teng, Separator based
parallel divide and conquer in computational geometry, SPAA 92 (1992).
- FS82
-
Charles D. Feustel and Linda G. Shapiro, The nearest neighbor problem in
an abstract metric space, Pattern Recognition Letters (1982).
- Fuk75
-
Keinosuke Fukunaga, A branch and bound algorithm for computing k-nearest
neighbors, IEEE Transactions on Computers (1975).
- Fuk90
-
Keinosuke Fukunaga, Introduction to statistical pattern recognition,
second ed., Academic Press, Inc., 1990.
- IM98
-
Piotr Indyk and Rajeev Motwani, Approximate nearest neighbors: Towards
removing the curse of dimensionality, Proc. 30th ACM STOC, 1998,
pp. 604-613.
- Kle97
-
Jon M. Kleinberg, Two algorithms for nearest-neighbor search in high
dimensions, Proc. 29th ACM STOC, 1997, pp. 599-608.
- KOR98
-
Eyal Kushilevitz, Rafail Ostrovsky, and Yuval Rabani, Efficient search
for approximate nearest neighbors in high dimensional spaces, Proc. 30th ACM
STOC, 1998, pp. 614-623.
- KP86
-
Baek S. Kim and Song B. Park, A fast nearest neighbor finding algorithm
based on the ordered partition, IEEE Transactions on Pattern Analysis and
Machine Intelligence 8 (1986), no. 6.
- MA99
-
David Mount and Sunil Arya, Ann: Library for approximate nearest neighbor
searching, http://www.cs.umd.edu/~mount/ANN/, 1999, Version 0.2 (Beta
release).
- Riv74
-
Ronald L. Rivest, On the optimality of Elias's algorithm for performing
best-match searches, Information Processing 74 (1974).
- RP92
-
V. Ramasubramanian and K. K. Paliwal, An efficient
approximation-elimination algorithm for fast nearest-neighbor search based on
a spherical distance coordinate formulation, Pattern Recognition Letters
13 (1992), 471-480.
- Sha77
-
Marvin Shapiro, The choice of reference points in best match file
searching, Communications of the ACM 20 (1977), no. 5.
- Uhl91a
-
Jeffrey K. Uhlmann, Metric trees, Applied Mathematics Letters 4
(1991), no. 5.
- Uhl91b
-
Jeffrey K. Uhlmann, Satisfying general proximity/similarity queries with
metric trees, Information Processing Letters (1991).
- Vai89
-
Pravin M. Vaidya, An O(n log n) algorithm for the
all-nearest-neighbor problem, Discrete & Computational Geometry 4
(1989), no. 2, 101-115.
- Yia93
-
Peter N. Yianilos, Data structures and algorithms for nearest neighbor
search in general metric spaces, Proceedings of the Fifth Annual ACM-SIAM
Symposium on Discrete Algorithms (SODA), 1993.
- Yia99
-
Peter N. Yianilos, Excluded middle vantage point forests for nearest
neighbor search, Tech. report, NEC Research Institute, 1999, Presented at
the Sixth DIMACS Implementation Challenge: Near Neighbor Searches workshop,
January 15, 1999.
- Yia00
-
Peter N. Yianilos, Locally lifting the curse of dimensionality for
nearest neighbor search, Proceedings of the Eleventh Annual ACM-SIAM
Symposium on Discrete Algorithms (SODA), 2000, pp. 361-370.
- Yun76
-
Thomas P. Yunck, A technique to identify nearest neighbors, IEEE
Transactions on Systems, Man, and Cybernetics (1976).
Locally Lifting the Curse of Dimensionality for
Nearest Neighbor Search
This document was generated using the
LaTeX2HTML translator Version 2K.1beta (1.47)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -image_type gif -nonext_page_in_navigation -noprevious_page_in_navigation -up_url ../main.html -up_title 'Publication homepage' -accent_images textrm -numbered_footnotes vp3.tex
The translation was initiated by Peter N. Yianilos on 2002-06-24
Footnotes
- ...
1
- Completed during 1999 while visiting the
Princeton University computer science department.
- ...12
- A preliminary version appeared as [Yia00].
- ... dimension3
- Measured as
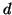 -dimensional
inner product operations
-dimensional
inner product operations
- ... cost4
- In
addition to the space required to store the dataset itself
- ... point.5
- The first of these may be
viewed as the second in the limit as a vantage point
moves toward infinity along the direction of the unit vector.
- ... data6
- That is, where the dataset is first transformed
to the coordinate system induced by a random basis. When the
kd-tree cuts space using a single coordinate in this
transformed setting, is then the same as cutting based the
inner product of a data element with a particular basis
vector.
- ...
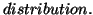 7
7
- Negligible dependence results from the
hypercube's corners, but for simplicity we ignore this effect.
- ... performed.8
- We must have
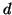 large enough to allow independent unit vectors to be
drawn, and will say more about this later.
large enough to allow independent unit vectors to be
drawn, and will say more about this later.
- ... increases9
- However it may increase somewhat before
eventually decreasing.
Up: Publication homepage
Peter N. Yianilos
2002-06-24
![]() with uniform
distributions, and the additional natural assumption
that the nearest neighbor is located within a constant
fraction
with uniform
distributions, and the additional natural assumption
that the nearest neighbor is located within a constant
fraction ![]() of the maximum interpoint distance in this space,
i.e. within distance
of the maximum interpoint distance in this space,
i.e. within distance ![]() of the query.
of the query.
![]() -dimensional inner product operations, is i)
strongly sublinear with respect to the data set size
-dimensional inner product operations, is i)
strongly sublinear with respect to the data set size
![]() for moderate
for moderate ![]() , ii) asymptotically, and as a
practical matter, independent of dimension.
, ii) asymptotically, and as a
practical matter, independent of dimension.
![]() of some database element, and
a randomly constructed data structure, the search
succeeds with a specified probability, which is a
parameter of the search algorithm. On average a
search performs
of some database element, and
a randomly constructed data structure, the search
succeeds with a specified probability, which is a
parameter of the search algorithm. On average a
search performs
![]() distance computations
where
distance computations
where ![]() is the number of points in the database,
and
is the number of points in the database,
and ![]() is calculated in our analysis. Linear
and near-linear space structures are described, and
our algorithms and analysis are free of large hidden
constants, i.e. the algorithms perform far less work
than exhaustive search - both in theory and practice.
is calculated in our analysis. Linear
and near-linear space structures are described, and
our algorithms and analysis are free of large hidden
constants, i.e. the algorithms perform far less work
than exhaustive search - both in theory and practice.