Up: Publication homepage
Excluded Middle Vantage Point Forests for Nearest Neighbor Search
Peter N. Yianilos1
July 20, 1998
Abstract:
Keywords: Nearest neighbor search,
Vantage point tree (vp-tree),
kd-tree,
Computational geometry,
Metric space.
We consider the radius-limited nearest neighbor problem in a metric
space. That is, given an 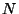 point dataset and a radius of interest
point dataset and a radius of interest
 , produce a data structure and associated search algorithm to
rapidly locate the dataset point nearest to any query
, produce a data structure and associated search algorithm to
rapidly locate the dataset point nearest to any query 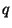 . Our focus
is on practical data structures that provide worst-case search time
bounds.
. Our focus
is on practical data structures that provide worst-case search time
bounds.
Vantage point trees (vp-trees) [32] and kd-trees
[15,16,4,3]
organize an 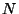 point dataset so that sublinear time nearest neighbor
searches may be performed on an expected basis for some fixed
distribution. Performance depends on the dataset and on the assumed
distribution of queries.
point dataset so that sublinear time nearest neighbor
searches may be performed on an expected basis for some fixed
distribution. Performance depends on the dataset and on the assumed
distribution of queries.
The excluded middle vantage point forest (vp-forest) is a new related
data structure that supports worst case sublinear time searches
for nearest neighbors within a fixed radius  of arbitrary
queries. Worst case performance depends on the dataset but is not
affected by the distribution of queries.
of arbitrary
queries. Worst case performance depends on the dataset but is not
affected by the distribution of queries.
The dataset is organized into a forest of 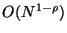 trees, each
of depth
trees, each
of depth 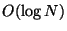 . Here
. Here 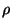 may be viewed as depending on
may be viewed as depending on
 , the distance measure, and on the dataset. The radius of
interest
, the distance measure, and on the dataset. The radius of
interest  is an input to the organization process and the result
is a data structure specialized to answer queries within this
distance.
is an input to the organization process and the result
is a data structure specialized to answer queries within this
distance.
Each element of the dataset occurs in exactly one tree so that the
entire forest remains linear space. Searches follow a single
root-leaf path in each tree. There is no backtracking when the search
is limited to neighbors within distance  . Along its way every neighbor within
. Along its way every neighbor within  is necessarily encountered. The query's
effect is to guide the descent through each tree.
is necessarily encountered. The query's
effect is to guide the descent through each tree.
There are no significant ancillary computational burdens at search
time. So upon creating the forest, the user simply adds the depths of
each tree in the forest to arrive at the maximum number of distance
evaluations each search will require. Each tree may be searched
independently. Searches then require 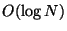 time given one
processor for each tree in the forest.
time given one
processor for each tree in the forest.
We also discuss design variations that trade space for reductions in
search time -- and compare forests with single trees constructed
similarly.
The general idea behind vp-forests is easily understood. Both
vp-trees and kd-trees recursively divide the dataset. At each node
the remaining dataset elements have an associated value, and the node
has a corresponding fixed threshold that is roughly central in the
distribution of values. Elements below this threshold are assigned
to, say, the left child, and those above to the right. For kd-trees
these values are those of individual coordinates within each data
vector. For vp-trees they are the distance of a metric space element
to some fixed vantage point.
Elements near to the threshold lead to backtracking during search.
When building a vp-forest, such elements are deleted from the tree and
added instead to a bucket. Once the tree is complete, the
bucket is organized into a tree in the same way, resulting in another
(smaller) bucket of elements. This continues until the forest is
built. This effectively eliminates backtracking. Because elements
near to the threshold are recursively deleted, and this threshold lies
near the middle of the distribution of values, we refer to our data
structure as an excluded middle vantage point forest. Both
vp-trees and kd-trees may be regarded as trivial instances of
vp-forests with no excluded middle.
We present an idealized analysis that allows us to predict vp-forest
performance in simple settings such as 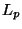 spaces with uniform
random datasets. Experiments are reported that confirm these
predictions. One contribution of this analysis is an interesting new
perspective on the so called curse of dimensionality (that is
that nearest neighbor search increases in difficulty with dimension).
In Euclidean space given a uniform random dataset drawn from the
hypercube, we observe that the worst-case difficulty of vp-forest
search for any fixed
spaces with uniform
random datasets. Experiments are reported that confirm these
predictions. One contribution of this analysis is an interesting new
perspective on the so called curse of dimensionality (that is
that nearest neighbor search increases in difficulty with dimension).
In Euclidean space given a uniform random dataset drawn from the
hypercube, we observe that the worst-case difficulty of vp-forest
search for any fixed  ought to be asymptotically constant with
respect to dimension -- and our experiments confirm this. Using
ought to be asymptotically constant with
respect to dimension -- and our experiments confirm this. Using
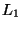 we expect constant difficulty if
we expect constant difficulty if  is allowed to increase
with
is allowed to increase
with 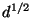 (
(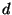 denotes dimension), and this too is confirmed by
experiment.
denotes dimension), and this too is confirmed by
experiment.
Our analysis also suggests that kd-trees should exhibit the same
dimension invariance for fixed search radii, and experiments confirm
this. For a worst case query, kd-tree search visits essentially
the entire dataset, but on average performs far less
work than the vp-forest.
The vp-forests described in this report stimulated the developments of
[33], but do not themselves appear to have immediate
practical value.
We conclude our introduction with a brief discussion of the nearest
neighbor search problem and literature. See [32] for
additional discussion.
Nearest neighbor search is an important task for non-parametric
density estimation, pattern recognition, information retrieval,
memory-based reasoning, and vector quantization. See
[11] for a survey.
The notion of a mathematical metric space [20] provides
a useful abstraction for nearness. Examples of metric spaces
include Euclidean space, the Minkowski 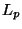 spaces, and many others.
Exploiting the metric space triangle inequality to eliminate points
during nearest neighbor search has a long history. Our work belongs
to this line. This paper extends it by i) introducing structures that
give worst case time bounds for limited radius searches, ii) providing
analysis for them, iii) introducing a method for trading space for
time, and iv) defining our data structures and algorithms in terms of
abstract projectors, which combines approaches that use distance
from a distinguished element with those such as kd-trees that use the
value of a distinguished coordinate.
spaces, and many others.
Exploiting the metric space triangle inequality to eliminate points
during nearest neighbor search has a long history. Our work belongs
to this line. This paper extends it by i) introducing structures that
give worst case time bounds for limited radius searches, ii) providing
analysis for them, iii) introducing a method for trading space for
time, and iv) defining our data structures and algorithms in terms of
abstract projectors, which combines approaches that use distance
from a distinguished element with those such as kd-trees that use the
value of a distinguished coordinate.
In early work Burkhard and Keller [7] describe
methods for nearest neighbor retrieval by evaluating distances from
distinguished elements. Their data structures are multi-way trees
corresponding to integral valued metrics.
Fukunaga in [18,19] exploits clustering
techniques [27] to produce a hierarchical decomposition
of Euclidean Space. During a branch and bound search, the triangle
inequality is used to rule out an entire cluster if the query is far
enough outside of it. While exploring a cluster he observes that the
triangle inequality may be used to eliminate some distance
computations. A key point missed is that when the query is well
inside of a cluster, the exterior need not be searched.
Collections of graphs are considered in [14] as an
abstract metric space with a metric assuming discrete values only.
This work is related to the constructions of [7]. In
their concluding remarks the authors clearly anticipate generalization
to continuous settings such as
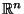 .
.
The idea that vantage points near the corners of the space are
better than those near the center was described in [28]
and much later in [32].
More recent papers describing vantage-point approaches are
[30,29,25] and [32] who
describe variants of what we refer to as a vantage-point tree. Also
see [10] for very recent work on search in metric spaces.
The well-known kd-tree of Friedman and Bentley
[15,16,4,3]
recursively divides a pointset in
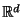 by projecting each element
onto a distinguished coordinates. Improvements, distribution
adaptation, and incremental searches, are described in
[13], [21], and [6]
respectively. In our framework kd-trees correspond to unit
vector projection with the canonical basis.
by projecting each element
onto a distinguished coordinates. Improvements, distribution
adaptation, and incremental searches, are described in
[13], [21], and [6]
respectively. In our framework kd-trees correspond to unit
vector projection with the canonical basis.
More recently, the Voronoi digram [2] has
provided a useful tool in low- dimensional Euclidean settings
- and the overall field and outlook of Computational Geometry
has yielded many interesting results such as those of
[31,9,8,17] and
earlier [12]. It appears that
[12] may be the first work focusing on worst
case bounds.
Very recently Kleinberg [22] gives two algorithms for an
approximate form of the nearest neighbor problem. The space
requirements of the first are prohibitive but the second, which almost
always finds approximate nearest neighbors seems to to be of more
practical interest. The recent work reported in [1] also
considers an approximate form of the problem. Their analysis gives
exponential dependence on 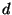 but the heuristic version of their
approach they describe may be of practical interest.
but the heuristic version of their
approach they describe may be of practical interest.
For completeness, early work dealing with two special cases
should be mentioned. Retrieval of similar binary keys is
considered by Rivest in [26] and the 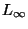 setting is the focus of [34].
setting is the focus of [34].
See [5] for worst case data structures for the range
search problem. This problem is related to but distinct from nearest
neighbor search since a neighbor can be nearby even if a single
coordinate is distant. But the 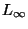 nearest neighbor problem
may be viewed as an instance of range search. Their paper also
describes a particular approach to trading space for time via an
overlapping cover. Our discussion of this topic in section 5
also takes this general approach.
nearest neighbor problem
may be viewed as an instance of range search. Their paper also
describes a particular approach to trading space for time via an
overlapping cover. Our discussion of this topic in section 5
also takes this general approach.
Vantage Point Forests
We begin by formalizing the ideas and construction sketched in the introduction.
Definition 1
Consider an ordered set
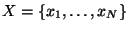
and a value
![$m \in [0,1]$](img39.gif)
. Let
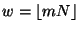
and
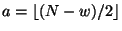
. Then the
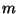
-split of
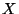
consists of left, middle, and
right subsets defined by:
That is, a balanced 3-way partition of 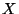 with
a central proportion of approximately
with
a central proportion of approximately 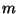 .
.
Definition 2
We refer to the result of algorithm
1 as the
idealized excluded middle vantage point forest induced by
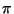
with central proportion
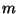
. When
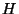
is a metric space and
the projection functions
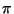
satisfy
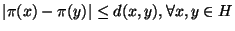
, this forest is of use for
nearest neighbor search and we further define

to be one
half of the minimum diameter of a middle set discarded during
construction.
We remark that each tree of the forest may be viewed as analogous to
the Cantor set from real analysis. That is, the subset of ![$[0,1]$](img68.gif) constructed by removing the central third of the interval -- and
proceeding recursively for both the left and right thirds. Our forest
then corresponds to a decomposition of the space into a union of
Cantor sets.
constructed by removing the central third of the interval -- and
proceeding recursively for both the left and right thirds. Our forest
then corresponds to a decomposition of the space into a union of
Cantor sets.
Two important examples of a suitable family of 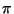 functions are
vantage point projection for general metric spaces, and unit vector projection for Euclidean space.
functions are
vantage point projection for general metric spaces, and unit vector projection for Euclidean space.
A vantage point projector 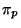 is defined for any
is defined for any 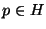 by
by
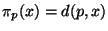 . The split points in tree construction correspond
to abstract spheres about
. The split points in tree construction correspond
to abstract spheres about 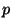 . It is easily verified that
. It is easily verified that
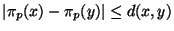 as required. The range of this projector is
the nonnegative reals. Letting
as required. The range of this projector is
the nonnegative reals. Letting  gives rise to a vantage
point tree [32].
gives rise to a vantage
point tree [32].
The unit vector projector 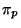 is defined for any
is defined for any 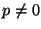 as
as
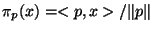 . This is easily seen to satisfy the required
inequality as well, and its range is not limited to nonnegative
values. Here the split points correspond to hyperplanes. Choosing
. This is easily seen to satisfy the required
inequality as well, and its range is not limited to nonnegative
values. Here the split points correspond to hyperplanes. Choosing
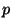 as canonical unit vectors and letting
as canonical unit vectors and letting 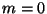 builds a form of
kd-tree [15,16,4,3].
It is important to note that
builds a form of
kd-tree [15,16,4,3].
It is important to note that 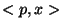 may be computed more rapidly for
canonical unit vectors -- in constant time with respect to
dimension. Also, we remark that whenever orthogonal vectors are used,
projection distances are, in a sense, additive, and that this fact can
be exploited (as kd-trees do) when designing solutions specialized for
may be computed more rapidly for
canonical unit vectors -- in constant time with respect to
dimension. Also, we remark that whenever orthogonal vectors are used,
projection distances are, in a sense, additive, and that this fact can
be exploited (as kd-trees do) when designing solutions specialized for
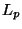 spaces. We do not consider either of these optimizations in this
paper.
spaces. We do not consider either of these optimizations in this
paper.
proof: At each step in the construction the central proportion of
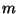 elements is removed so that the left and right subsets are
each of size
elements is removed so that the left and right subsets are
each of size 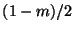 . The first tree's depth is then
. The first tree's depth is then
![$[1/log_2(2/(1-m))] log_2 N = \Theta(\log N)$](img85.gif) . So the number of
elements left in the tree is
. So the number of
elements left in the tree is
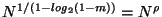 .
.
The number of elements left after the first tree has been
constructed is then 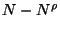 . After the second
. After the second
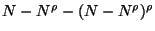 are left, and so on. Clearly
are left, and so on. Clearly
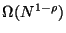 trees are required to reduce the
population to any fixed size.
trees are required to reduce the
population to any fixed size.
Once the population has been reduced to 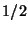 of its original
size, the number of elements removed as each tree is built
will have declined to
of its original
size, the number of elements removed as each tree is built
will have declined to
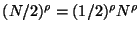 . Since
. Since
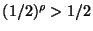 no fewer than
no fewer than 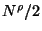 are removed. So
the number of steps required to reach
are removed. So
the number of steps required to reach 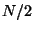 is no more than
is no more than
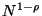 . The number required to reach
. The number required to reach 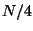 is then
is then
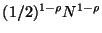 -- and so on forming a geometric
series. So the number required to reach any fixed level is
-- and so on forming a geometric
series. So the number required to reach any fixed level is
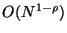 . The number of trees in the forest is then
. The number of trees in the forest is then
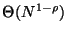 -- and the total space is clearly
linear.
-- and the total space is clearly
linear.
A search for nearest neighbors within distance  is then
made by following a single root-leaf path in each tree
establishing the required time bound. Each tree can be
considered independently and the results merged to arrive
at a single nearest neighbor. This establishes the
stated parallel complexity.
is then
made by following a single root-leaf path in each tree
establishing the required time bound. Each tree can be
considered independently and the results merged to arrive
at a single nearest neighbor. This establishes the
stated parallel complexity.
Finally we consider organizational time. The first level of
the first tree requires 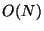 work to produce projection
values of each point in the space, and then
work to produce projection
values of each point in the space, and then 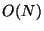 time to
effect the split (linear time order statistics). The next
level considers a total of
time to
effect the split (linear time order statistics). The next
level considers a total of 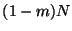 records, and so on,
leading to
records, and so on,
leading to 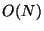 overall time from which the stated
organization time bound follows.
overall time from which the stated
organization time bound follows.
For example, if 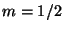 there are
there are 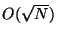 trees in the forest,
and search time is
trees in the forest,
and search time is
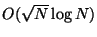 . Organization requires
. Organization requires
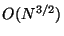 time, but as always only
time, but as always only 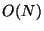 space is consumed. As
space is consumed. As
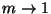 we expect
we expect  to increase but the number of trees
approaches
to increase but the number of trees
approaches 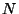 and searches come ever closer to examining every point.
As
and searches come ever closer to examining every point.
As
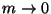 we expect
we expect  to decrease while search time
approaches the logarithmic ideal. The
to decrease while search time
approaches the logarithmic ideal. The 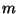 parameter then, in a sense,
interpolates between exhaustive large-
parameter then, in a sense,
interpolates between exhaustive large- search, and logarithmic
small-
search, and logarithmic
small- search.
search.
Our development above is very general and describes idealized
forests. We now explain in what sense they are idealized and begin
our discussion of concrete settings.
Algorithm 1 removes a fixed central proportion of the
points as each tree node is processed. This simplifies analysis but,
because  is defined as the minimum diameter of all such central
cuts,
is defined as the minimum diameter of all such central
cuts,  might wind up too small to be of any practical value.
Also, the projection function will not in general be 1-1, and this
detail must be considered in any implementation.
The user's objective is a satisfactory tradeoff between the
conflicting goals of minimizing search time, and maximizing
might wind up too small to be of any practical value.
Also, the projection function will not in general be 1-1, and this
detail must be considered in any implementation.
The user's objective is a satisfactory tradeoff between the
conflicting goals of minimizing search time, and maximizing  .
.
One approach is to minimize search time given a lower bound on  .
In contrast with the idealized case, here it makes sense to cut a
variable central proportion -- one of diameter
.
In contrast with the idealized case, here it makes sense to cut a
variable central proportion -- one of diameter 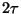 . Notice in
this case that the construction recursion may terminate before
reaching a single node. Since the choice of projector may affect this
proportion, it may be wise to invest additional time during
construction to evaluate multiple projectors. This corresponds to the
idea of selecting a vantage point for a vp-tree, or a cut-dimension
for a kd-tree. When fixed diameter cuts are made a more complicated
stopping rule for forest construction is needed. Otherwise
a tiny ball of points, smaller than
. Notice in
this case that the construction recursion may terminate before
reaching a single node. Since the choice of projector may affect this
proportion, it may be wise to invest additional time during
construction to evaluate multiple projectors. This corresponds to the
idea of selecting a vantage point for a vp-tree, or a cut-dimension
for a kd-tree. When fixed diameter cuts are made a more complicated
stopping rule for forest construction is needed. Otherwise
a tiny ball of points, smaller than 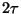 in diameter, will never
be assigned to any tree.
in diameter, will never
be assigned to any tree.
It is also important to note that while our focus is on worst case
performance, and there is no backtracking required to search for
neighbors within distance  , that backtracking can be performed
as for vp-trees or kd-trees in order to satisfy queries beyond
, that backtracking can be performed
as for vp-trees or kd-trees in order to satisfy queries beyond  .
.
Another difference between our idealized construction and practical
implementations is that in the idealized case points are stored only
at tree leaves.
In the vp-tree case the projector is formed by selecting an element 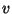 of
subspace
of
subspace 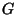 and computing its distance to the query
and computing its distance to the query 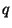 and to every
other element of
and to every
other element of 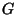 . Having computed its distance to the query, there
is no need to examine
. Having computed its distance to the query, there
is no need to examine 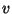 again, and we therefore view it as stored at
the interior tree node at which is was used. So the difference is that
the set
again, and we therefore view it as stored at
the interior tree node at which is was used. So the difference is that
the set 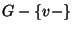 is split at each level of the recursion.
When using unit vector projection it is also possible to use an element
is split at each level of the recursion.
When using unit vector projection it is also possible to use an element 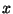 of
the database. Here too, it is unnecessary to examine
of
the database. Here too, it is unnecessary to examine 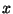 again since
again since
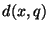 is easily computed given
is easily computed given 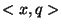 .
.
The Minkowski 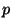 -norm is denoted
-norm is denoted 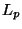 and defined by
and defined by
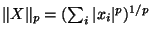 for
for 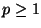 . A metric results from
evaluating the norm of the difference of two vectors. The Euclidean
metric is
. A metric results from
evaluating the norm of the difference of two vectors. The Euclidean
metric is 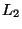 , the city block metric is
, the city block metric is 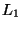 , and by
convention
, and by
convention 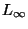 gives the maximum absolute value over individual
coordinates.
gives the maximum absolute value over individual
coordinates.
We begin with an asymptotic statement that allows to understand the
expected performance of excluded middle vantage point forests in high
dimensional instances of these spaces given distributions such as the
uniform one.
Proposition 2
Let
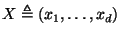
be a vector of
i.i.d. random variables. Consider
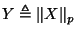
and let
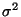
denote the variance of
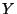
about its mean.
Then
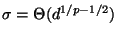
regarding
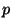
is fixed
and letting
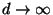
.
proof: Consider
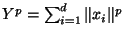 . Because the
. Because the 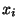 are i.i.d. both the mean and variance of
are i.i.d. both the mean and variance of 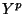 scale linearly
with
scale linearly
with 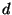 . So relative to the magnitude of the mean of
. So relative to the magnitude of the mean of 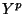 , its
standard deviation shrinks as
, its
standard deviation shrinks as 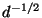 , whence the
distribution of
, whence the
distribution of 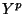 values is increasingly concentrated
about its mean. Taking the
values is increasingly concentrated
about its mean. Taking the 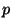 th root to arrive at
th root to arrive at 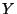 has
the effect of scaling all of these values downward by a factor of
approximately
has
the effect of scaling all of these values downward by a factor of
approximately
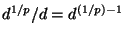 so the variance
changes by a factor of
so the variance
changes by a factor of 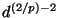 . But the variance of
. But the variance of
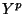 scales with
scales with 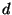 , so the variance of
, so the variance of 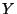 scales with
scales with
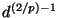 , and its standard deviation with
, and its standard deviation with
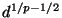 .
.
To keep its statement simple the proposition includes an i.i.d.
assumption, but less is necessary. Independence is required but the
mean and variance of each variable 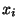 need not be the same. It is
merely necessary that the mean and variance of
need not be the same. It is
merely necessary that the mean and variance of 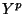 scales
approximately linearly with
scales
approximately linearly with 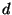 .
.
The proposition is then relevant because of two observations about
uniformly distributed high dimensional 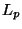 spaces. Firstly, that
choosing a point
spaces. Firstly, that
choosing a point 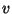 at random, the distribution of
at random, the distribution of 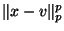 over
over
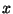 in the space exhibits the required linear scaling behavior.
Secondly, that making cuts during construction (whether spherical or
hyperplanar) in a high dimensional space, leaves subspaces that for
the purposes of this proposition still behave like uniformly random
ones. The same is true for unit vector projection.
in the space exhibits the required linear scaling behavior.
Secondly, that making cuts during construction (whether spherical or
hyperplanar) in a high dimensional space, leaves subspaces that for
the purposes of this proposition still behave like uniformly random
ones. The same is true for unit vector projection.
For Euclidean space (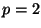 ) we then expect
) we then expect 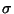 to be
asymptotically constant with dimension. Then the distribution of
values the construction algorithm is presented with at each step,
becomes the same for sufficiently high dimension. For
to be
asymptotically constant with dimension. Then the distribution of
values the construction algorithm is presented with at each step,
becomes the same for sufficiently high dimension. For 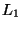 we have
that
we have
that 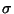 scales upward with
scales upward with 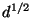 , and for
, and for 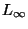 it
scales downward with
it
scales downward with 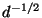 . The result is that we expect the
following behavior when using excluded middle vantage point forests to
search uniformly distributed point sets:
. The result is that we expect the
following behavior when using excluded middle vantage point forests to
search uniformly distributed point sets:
- The worst-case time to search for the nearest neighbor
within distance
 of a query under the Euclidean metric,
is constant with respect to dimension.
of a query under the Euclidean metric,
is constant with respect to dimension.
- Using
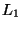 the task becomes easier with increasing dimension, or,
one can scale
the task becomes easier with increasing dimension, or,
one can scale  upward with
upward with 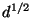 and maintain constant
time.
and maintain constant
time.
- For
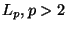 the task becomes harder with increasing
dimension. Interestingly, in the limiting
the task becomes harder with increasing
dimension. Interestingly, in the limiting 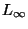 case,
our approach is essentially worthless but range search
techniques apply because a search for neighbors within
case,
our approach is essentially worthless but range search
techniques apply because a search for neighbors within  is just a range query of this form applying to every
dimension.
is just a range query of this form applying to every
dimension.
Finally we remark that
the case of unit vector projection in Euclidean space directly leads to
the first observation above without the proposition.
We have implemented our ideas as an ANSI-C program. Figures
1 and 2 describe experiments which confirm the
behavior above for 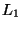 and
and 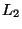 .
It is important to reiterate that searching the forest involves no decisions
or backtracking, so that search time is essentially constant.
So:
.
It is important to reiterate that searching the forest involves no decisions
or backtracking, so that search time is essentially constant.
So:
- Our experiments reflect the time required to perform the search
for any given query.
- Because of the nature of the search, all neighbors within
 will necessarily be encountered during it.
will necessarily be encountered during it.
Other experiments confirmed the
expected behavior when 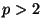 . Vantage point projection is used but
unit vector projection gives similar results.
A vantage point is selected at random from the current subset of the dataset.
The implementation
forces fixed
. Vantage point projection is used but
unit vector projection gives similar results.
A vantage point is selected at random from the current subset of the dataset.
The implementation
forces fixed  cuts and stops forest construction when
all remaining points are failed to be assigned to a tree after
a large number of attempts. These points are then stored as a simple
list. The implementation also stores points at interior nodes, not
just at leaves.
Finally, its splitting algorithm is general, i.e. does
not assume 1-1 projection functions.
cuts and stops forest construction when
all remaining points are failed to be assigned to a tree after
a large number of attempts. These points are then stored as a simple
list. The implementation also stores points at interior nodes, not
just at leaves.
Finally, its splitting algorithm is general, i.e. does
not assume 1-1 projection functions.
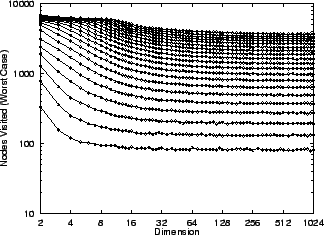
Figure 1:
The worst-case number of nodes visited
by an excluded middle vantage point
forest search under the 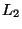 metric
metric
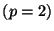 , the uniform distribution
(10,000 points), and fixed
, the uniform distribution
(10,000 points), and fixed  radius, does not in the limit depend
on dimension. The curves depicted
from bottom to top correspond to
central exclusion widths from
radius, does not in the limit depend
on dimension. The curves depicted
from bottom to top correspond to
central exclusion widths from 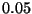 to
to 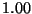 in increments of
in increments of 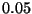 .
Corresponding
.
Corresponding  values are half
as large.
values are half
as large.
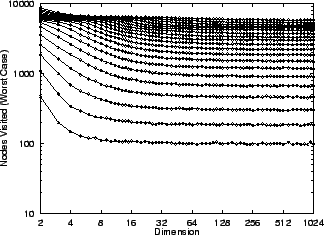 |
Figure 2:
For the 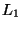 metric
metric 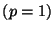 and the
setting of figure 1,
dimension invariance is observed if
central exclusion widths are scaled by
and the
setting of figure 1,
dimension invariance is observed if
central exclusion widths are scaled by
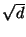 . For example, the
bottom curve corresponds to
. For example, the
bottom curve corresponds to
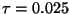 for
for 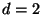 and
and
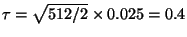 for
for
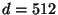 . So for
. So for 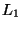 the search
radius may increase with dimension
while holding worst-case performance
constant.
the search
radius may increase with dimension
while holding worst-case performance
constant.
 |
The uniform random case is, of course, of little practical interest.
While we give no general worst case bounds it is important to note
that performing a fixed  construction will always generate a
forest, and a corresponding query-independent worst case bound on
search time for that particular point set.
construction will always generate a
forest, and a corresponding query-independent worst case bound on
search time for that particular point set.
We compare performance in our setting with kd-tree search
[15,16,4,3],
adapted from [23] as described in [33]
for radius limited search.
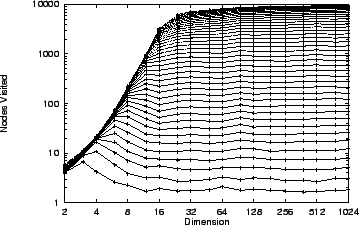
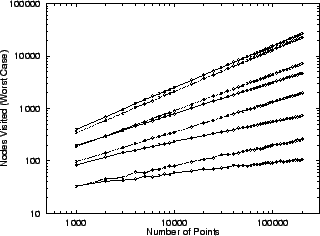
Figure 3 shows the result of our experiment. The
same dimensional invariance is evident, but now with respect
to expected search time. As for our worst-case
structures, this follows from our earlier observations about
projection distributions in high dimensional spaces. The
figure shows that expected search complexity is somewhat lower
than the worst case results of figure 1 where
saturation is evident exclusion width 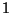 is approached. For
kd-trees, saturation is delayed until roughly width
is approached. For
kd-trees, saturation is delayed until roughly width 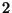 .
.
The expected kd-tree search times are much lower than the
worst case values of figure 1. In fact, given
random queries, the probability is vanishingly small that
kd-tree search will cost as much as our worst case search.
In the uniform case a query at the center of the hypercube is
costly for the kd-tree, and we have confirmed that essentially
the entire dataset is searched in this case. We observe that
one might build a pair of kd-trees whose cut points are offset
to eliminate these hot spots and perhaps even provide
worst case performance bounds in the radius-limited case.
Figure 3:
The average number of nodes visited
by kd-tree search
under the 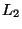 metric
metric
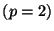 , the uniform distribution
(10,000 points), and fixed
, the uniform distribution
(10,000 points), and fixed  radius, does not in the limit depend
on dimension. The curves depicted
from bottom to top correspond to
central exclusion widths from
radius, does not in the limit depend
on dimension. The curves depicted
from bottom to top correspond to
central exclusion widths from 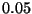 to
to 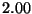 in increments of
in increments of 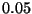 .
Corresponding
.
Corresponding  values are half
as large.
values are half
as large.
 |
By slightly modifying the forest construction algorithm one
can build a single 3-way tree. Instead of adding the central
elements to a bucket for later use in building the next tree,
we instead leave them in place forming a third central branch.
To search such a tree one must follow two of the three
branches: either the left and middle, or the middle and right.
We remark that this tree structure was our first idea for
enhancing vantage point trees to provide worst-case
search time bounds.
Like the forest, this tree requires linear space, but a simple
example and analysis illustrates that its search performance is
usually much worse.
Consider the 3-way tree built by an equal 3-way division, i.e. where
the central exclusion proportion is 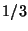 . Then the tree's
depth is
. Then the tree's
depth is 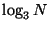 . The path taken by any single search
consists of a binary tree embedded within this trinary tree.
So
. The path taken by any single search
consists of a binary tree embedded within this trinary tree.
So
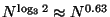 nodes will be visited.
But we have seen that a forest with exclusion proportion
nodes will be visited.
But we have seen that a forest with exclusion proportion 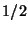 results in
results in
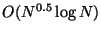 node visits, which is
superior despite the fact that the tree was built using
a smaller exclusion proportion (
node visits, which is
superior despite the fact that the tree was built using
a smaller exclusion proportion (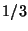 vs.
vs. 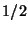 ).
).
Table 4 compares the performance of idealized
trees and forests for various database sizes and central
exclusion proportions. Figure 4 compares the
performance of actual trees and forests in a uniform
distribution Euclidean space setting. The results are
consistent with our analysis and the computations of table
4. We briefly remark that for small  ,
trees and forests with a higher branching factor make
sense. Here the projected point set is partitioned into
bands with alternating ones corresponding to the excluded
middle of our 3-way construction.
,
trees and forests with a higher branching factor make
sense. Here the projected point set is partitioned into
bands with alternating ones corresponding to the excluded
middle of our 3-way construction.
Table 1:
The relative search time ratio of an idealized excluded
middle vantage point forest, to that of a tree. The forest is better
in almost all cases. Notice that its relative advantage can be quite
large. The tree is preferred only in the case of large central
exclusion widths, and then by only a small factor.
| Central |
Number of Elements |
| Proportion |
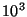 |
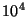 |
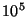 |
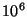 |
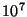 |
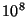 |
| 0.100 |
0.52 |
0.37 |
0.23 |
0.14 |
0.08 |
0.05 |
| 0.300 |
0.87 |
0.58 |
0.42 |
0.29 |
0.18 |
0.11 |
| 0.500 |
1.21 |
0.96 |
0.83 |
0.63 |
0.44 |
0.36 |
| 0.700 |
1.40 |
1.31 |
1.18 |
1.03 |
0.88 |
0.77 |
| 0.900 |
1.50 |
1.64 |
1.65 |
1.58 |
1.51 |
1.51 |
|
Figure 4:
A comparison of excluded-middle
vantage trees (dashed line) and
forests (solid line) for the 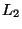 metric,
metric, 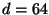 , the uniform
distribution, and central exclusion
widths of
, the uniform
distribution, and central exclusion
widths of
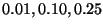 , and
, and
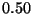 corresponding to the curve
pairs from bottom to top. For small
widths the forest performs better and
the advantage increases with database
size (see the difference in curve
slopes). This advantage reduces with
increasing exclusion width, and by
corresponding to the curve
pairs from bottom to top. For small
widths the forest performs better and
the advantage increases with database
size (see the difference in curve
slopes). This advantage reduces with
increasing exclusion width, and by
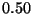 the tree is the winner.
the tree is the winner.
 |
Trading Space for Time
Until now we have considered linear space structures. In this
section we describe a general technique for trading space for
time. For analysis we will return to the idealized setting in
which construction removes fixed proportions -- not fixed
diameter central subsets as in the implementation and
experiments. This will allow us to make calculations intended
to illuminate the engineering tradeoffs one faces in practice.
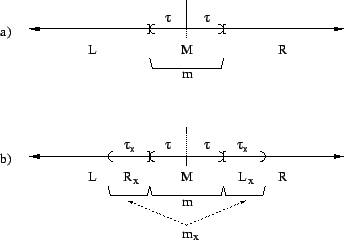
The 3-way split performed by algorithm 1 is
illustrated in figure 5(a). The central proportion
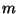 is imagined to correspond to some fixed radius
is imagined to correspond to some fixed radius  as
shown. We motivate the construction in terms of
as
shown. We motivate the construction in terms of  but
will analyze it in terms of
but
will analyze it in terms of 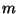 .
.
Figure 5:
a) An idealized illustration of the division according
to definition 1 of the projection of a point
set onto the real line. Subset 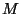 results from
removing the central proportion of
results from
removing the central proportion of 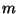 elements.
Assuming a symmetrical distribution set
elements.
Assuming a symmetrical distribution set 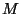 has
diameter
has
diameter 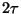 . Subset
. Subset 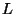 consists of everything
below
consists of everything
below 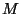 in projected value, and
in projected value, and 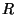 of everything
above it.
b) An idealized illustration of the tradeoff of space
for time. Here an additional proportion
of everything
above it.
b) An idealized illustration of the tradeoff of space
for time. Here an additional proportion 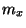 of central
elements encloses
of central
elements encloses 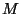 and corresponds to two subsets
and corresponds to two subsets
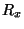 and
and 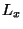 . Elements of
. Elements of 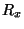 are stored in
are stored in 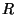 and also in
and also in 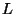 . Likewise elements of
. Likewise elements of 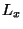 are stored
in both
are stored
in both 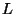 and
and 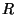 . The result is that the
effective search radius within which the worst case
time bound holds is extended from
. The result is that the
effective search radius within which the worst case
time bound holds is extended from  to
to
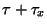 .
.
 |
When the projection of a query lies just to the right of the
dotted centerline, a search for a nearest neighbor within
 will explore
will explore 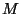 and
and 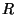 . Increasing
. Increasing  by
some value
by
some value 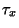 forces the search to explore
forces the search to explore 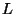 as well.
as well.
To avoid exploring all three we store the points in interval
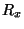 in two places (see figure 5(b)). First, they
are stored as always in
in two places (see figure 5(b)). First, they
are stored as always in 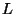 . Second, they are stored with
those of
. Second, they are stored with
those of 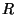 . As a result of this overlap only
. As a result of this overlap only 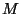 and
and 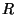 must be explored as before. Points in interval
must be explored as before. Points in interval 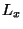 are
similarly stored twice.
are
similarly stored twice.
Continuing this modified division throughout forest construction
yields a data structure that:
- Includes the same number of trees as before, since
the size of the excluded central proportion is unchanged.
- Contains trees that are deeper, but still
asymptotically of logarithmic depth. Tree depth is
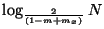 .
.
- The result is the same worst-case asymptotic search
times, but over the larger idealized radius
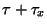 .
.
- Provides this search-time benefit at the cost of
space. The deeper tree has
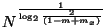 nodes.
Space for the entire forest is then:
nodes.
Space for the entire forest is then:
For example, let 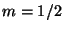 and
and 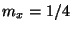 . Then space is
. Then space is
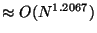 .
.
From another viewpoint the same space tradeoff may be used to
reduce search time for a fixed  . For example, an
ordinary
. For example, an
ordinary 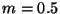 forest provides
forest provides
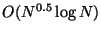 searches. Letting
searches. Letting 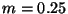 and
and 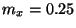 reduces the time
to
reduces the time
to
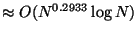 but space is increased from
but space is increased from
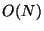 to
to
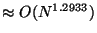 .
.
Finally consider the interesting extreme case where 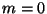 .
Here the forest consists of a single binary tree.
Search time is then
.
Here the forest consists of a single binary tree.
Search time is then 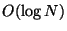 with space
with space
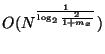 .
.
Excluded middle forests might be applied to problems other
than nearest neighbor search. They might, for example,
improve the effectiveness of decision trees, an important tool
for machine learning [24]. The motivation here
is that values near to the decision threshold may be more
difficult to classify based on the selected decision variable.
We now discuss several possibilities related to nearest
neighbor search.
For each fixed  our implementation generates a forest with
some associated worst case query time bound. Smaller
our implementation generates a forest with
some associated worst case query time bound. Smaller  values, in general, result in smaller bounds. Now suppose
that a forest is built with
values, in general, result in smaller bounds. Now suppose
that a forest is built with 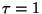 and the system is then
presented with a query. Next suppose that early in the
search a neighbor is encountered that is well within the
and the system is then
presented with a query. Next suppose that early in the
search a neighbor is encountered that is well within the
 radius, say at distance
radius, say at distance 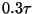 . Despite our
good fortune the remaining search will take no less time.
Root-leave paths in every remaining tree must be examined.
. Despite our
good fortune the remaining search will take no less time.
Root-leave paths in every remaining tree must be examined.
One idea is to build multiple forests. One for 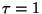 ,
and additional forests for
,
and additional forests for
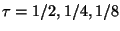 , etc.
Then upon encountering a point at distance
, etc.
Then upon encountering a point at distance 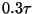 the
search algorithm might consider aborting its processing
of the
the
search algorithm might consider aborting its processing
of the 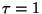 forest and switch over to the
forest and switch over to the 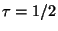 forest, which offers a better worst case time bound.
forest, which offers a better worst case time bound.
It is interesting to note that this decision to switch can be made
very easily by considering the number of points remaining in
the current forest, and comparing it to the worst case bound
for the new one. If the latter is smaller it makes sense to
switch over. Implementations may consider another factor
in their decisions. The distance from the query to
all points already visited might be remembered to avoid
unnecessary metric evaluations when processing restarts
at the beginning of a new forest.
Another topic for future work involves two settings in which
our methods seem far from optimal: boolean vectors with Hamming
distance, and the 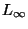 case.
case.
The boolean Hamming distance setting corresponds to 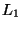 , and
the number of errors we can tolerate while maintaining
constant search complexity for the uniform distribution grows
with
, and
the number of errors we can tolerate while maintaining
constant search complexity for the uniform distribution grows
with 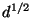 . But experiments suggest that our forests do
not compete in practice with a particular simple method. If
. But experiments suggest that our forests do
not compete in practice with a particular simple method. If
 is the maximum Hamming distance to be tolerated, this
method divides the high-dimensional vector into
is the maximum Hamming distance to be tolerated, this
method divides the high-dimensional vector into 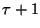 segments and exploits the fact that the dataset projected onto
one of these segments may be assumed to have Hamming distance
zero to the query. Simple hashing may then be used to
maintain these projections. We are interested in better
understanding the relationship of this simple technique to the
ideas of this paper. We remark that the same idea of
dimensional partitioning applies to any Minkowski metric, but
so far we can obtain an advantage only in the Boolean case.
segments and exploits the fact that the dataset projected onto
one of these segments may be assumed to have Hamming distance
zero to the query. Simple hashing may then be used to
maintain these projections. We are interested in better
understanding the relationship of this simple technique to the
ideas of this paper. We remark that the same idea of
dimensional partitioning applies to any Minkowski metric, but
so far we can obtain an advantage only in the Boolean case.
As described earlier, our methods grow weaker with growing
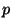 , becoming essentially useless for
, becoming essentially useless for 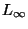 . This is
interesting since suddenly, with
. This is
interesting since suddenly, with 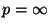 , the problem
becomes an instance of range search. We speculate that
ideas from range search might in some form be of use
before
, the problem
becomes an instance of range search. We speculate that
ideas from range search might in some form be of use
before 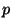 reaches
reaches 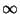 -- if only as an approximate
solution to the nearest neighbor problem.
-- if only as an approximate
solution to the nearest neighbor problem.
Finally we observe that in
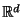 storing the data vectors
themselves requires
storing the data vectors
themselves requires 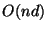 space. The tree/forest we build
can use
space. The tree/forest we build
can use 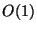 space pointers to these vectors. For this
reason we can tolerate super-linear space in the tree/forest,
namely
space pointers to these vectors. For this
reason we can tolerate super-linear space in the tree/forest,
namely 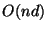 . We suggest that a practical implementation
for Euclidean space should take advantage of this and also
exploit the canonical/orthogonal basis optimizations mentioned
in section 2.
. We suggest that a practical implementation
for Euclidean space should take advantage of this and also
exploit the canonical/orthogonal basis optimizations mentioned
in section 2.
Our work towards a general and practical tool for nearest
neighbor search began with [32] and continues
with this paper.
We envision a high-level procedure that like the qsort()
function from the standard Unix library, views its underlying
database through a layer of abstraction. In the case of sorting,
a comparison function is provided. For nearest neighbor search
projection and distance computation must be supported.
Sorting is, however, a much simpler problem in as much as
practical algorithms exist with acceptable worst
case time and space complexity -- independent of the dataset.
For nearest neighbor search we suggest that a general tool
must be flexible and
support:
- User supplied metrics and projectors.
- The construction of dataset-specific solutions
giving worst-case query times for neighbors
within a specified distance.
- Heuristic backtracking searches beyond this distance.
- Control over the time invested in construction to
optimize the resulting data structure.
- Control over the time-space tradeoff. That is, the
ability to invest additional space to improve search
performance.
- Dynamic operation, i.e. the addition and deletion of
points from the data structure during use (not discussed
in this paper -- but clearly possible).
- The ability to exploit the
canonical/orthogonal basis optimizations for
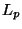 mentioned in section 2.
mentioned in section 2.
We hope that the ideas and results of this paper brings us closer
to the development of such a tool.
The author thanks Joe Kilian for helpful discussions.
- 1
-
ARYA, S., MOUNT, D., NETANYAHU, N., SILVERMAN, R., AND WU, A.
An optimal algorithm for approximate nearest neighbor searching in
fixed dimension.
In Proc. 5th ACM-SIAM SODA (1994), pp. 573-583.
- 2
-
AURENHAMMER, F.
Voronoi diagrams - a survey of a fundemental geometric data
structure.
ACM Computing Surveys 23, 3 (September 1991).
- 3
-
BENTLEY, J. L.
Multidimensional divide-and-conquer.
Communications of the ACM 23, 4 (April 1980).
- 4
-
BENTLEY, J. L., AND FRIEDMAN, J. H.
Data structures for range searching.
Computing Surveys (December 1979).
- 5
-
BENTLEY, J. L., AND MAURER, H. A.
Efficient worstcase data structures for range searching.
Acta Informatica 13, 2 (1980), 155-168.
- 6
-
BRODER, A. J.
Strategies for efficient incremental nearest neighbor search.
Pattern Recognition 23, 1/2 (1990).
- 7
-
BURKHARD, W. A., AND KELLER, R. M.
Some approaches to best-match file searching.
Communications of the ACM 16, 4 (April 1973).
- 8
-
CLARKSON, K. L.
New applications of random sampling in computational geometry.
Discrete & Computational Geometry 2 (1987), 195-222.
- 9
-
CLARKSON, K. L.
A randomized algorithm for closest-point queries.
SIAM Journal on Computing 17, 4 (August 1988).
- 10
-
CLARKSON, K. L.
Nearest neighbor queries in metric spaces.
In Proc. 29th ACM STOC (1997), pp. 609-617.
- 11
-
DASARATHY, B. V., Ed.
Nearest neighbor pattern classification techniques.
IEEE Computer Society Press, 1991.
- 12
-
DOBKIN, D., AND LIPTON, R. J.
Multidimensional searching problems.
SIAM Journal on Computing 5, 2 (June 1976).
- 13
-
EASTMAN, C. M., AND WEISS, S. F.
Tree structures for high dimensionality nearest neighbor searching.
Information Systems 7, 2 (1982).
- 14
-
FEUSTEL, C. D., AND SHAPIRO, L. G.
The nearest neighbor problem in an abstract metric space.
Pattern Recognition Letters (December 1982).
- 15
-
FRIEDMAN, J. H., BASKETT, F., AND SHUSTEK, L. J.
An algorithm for finding nearest neighbors.
IEEE Transactions on Computers (October 1975).
- 16
-
FRIEDMAN, J. H., BENTLEY, J. L., AND FINKEL, R. A.
An algorithm for finding best matches in logarithmic expected time.
ACM Transactions on Mathematical Software 3, 3 (September
1977).
- 17
-
FRIEZE, A. M., MILLER, G. L., AND TENG, S.-H.
Separator based parallel divide and conquer in computational
geometry.
SPAA 92 (1992).
- 18
-
FUKUNAGA, K.
A branch and bound algorithm for computing k-nearest neighbors.
IEEE Transactions on Computers (July 1975).
- 19
-
FUKUNAGA, K.
Introduction to Statistical Pattern Recognition, second ed.
Academic Press, Inc., 1990.
- 20
-
KELLY, J. L.
General Topology.
D. Van Nostrand, New York, 1955.
- 21
-
KIM, B. S., AND PARK, S. B.
A fast nearest neighbor finding algorithm based on the ordered
partition.
IEEE Transactions on Pattern Analysis and Machine Intelligence
8, 6 (November 1986).
- 22
-
KLEINBERG, J. M.
Two algorithms for nearest-neighbor search in high dimensions.
In Proc. 29th ACM STOC (1997), pp. 599-608.
- 23
-
MOUNT, D., AND ARYA, S.
Ann: Library for approximate nearest neighbor searching.
http://www.cs.umd.edu/~mount/ANN/, 1999.
Version 0.2 (Beta release).
- 24
-
QUINLAN, J. R.
Learning decision tree classifiers.
ACM Computing Surveys 28 (1996).
- 25
-
RAMASUBRAMANIAN, V., AND PALIWAL, K. K.
An efficient approximation-elimination algorithm for fast
nearest-neighbor search based on a spherical distance coordinate formulation.
Pattern Recognition Letters 13 (1992), 471-480.
- 26
-
RIVEST, R. L.
On the optimality of Elias's algorithm for performing best-match
searches.
Information Processing 74 (1974).
- 27
-
SALTON, G., AND WONG, A.
Generation and search of clustered files.
ACM Transactions on Database Systems (December 1978).
- 28
-
SHAPIRO, M.
The choice of reference points in best match file searching.
Communications of the ACM 20, 5 (May 1977).
- 29
-
UHLMANN, J. K.
Metric trees.
Applied Mathematics Letters 4, 5 (1991).
- 30
-
UHLMANN, J. K.
Satisfying general proximity/similarity queries with metric trees.
Information Processing Letters (November 1991).
- 31
-
VAIDYA, P. M.
An O(n log n) algorithm for the all-nearest-neighbor
problem.
Discrete & Computational Geometry 4, 2 (1989), 101-115.
- 32
-
YIANILOS, P. N.
Data structures and algorithms for nearest neighbor search in general
metric spaces.
In Proceedings of the Fifth Annual ACM-SIAM Symposium on
Discrete Algorithms (SODA) (1993).
- 33
-
YIANILOS, P. N.
Locally lifting the curse of dimensionality for nearest neighbor
search.
Tech. rep., NEC Research Institute, 4 Independence Way, June 1999.
- 34
-
YUNCK, T. P.
A technique to identify nearest neighbors.
IEEE Transactions on Systems, Man, and Cybernetics (October
1976).
Excluded Middle Vantage Point Forests for Nearest Neighbor Search
This document was generated using the
LaTeX2HTML translator Version 2K.1beta (1.47)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -image_type gif -nonext_page_in_navigation -noprevious_page_in_navigation -up_url ../main.html -up_title 'Publication homepage' -accent_images textrm -numbered_footnotes vp2.tex
The translation was initiated by Peter N. Yianilos on 2002-06-25
Footnotes
- ... Yianilos1
- The author is with NEC Research Institute,
4 Independence Way, Princeton, NJ. Email: pny@research.nj.nec.com
Up: Publication homepage
Peter N. Yianilos
2002-06-25
![]() spaces with uniform random datasets -- and
experiments confirm these predictions. Another contribution
of the analysis is a new perspective on the curse of
dimensionality in the context of our methods and kd-trees as
well. In our idealized setting the dataset is organized into
a forest of
spaces with uniform random datasets -- and
experiments confirm these predictions. Another contribution
of the analysis is a new perspective on the curse of
dimensionality in the context of our methods and kd-trees as
well. In our idealized setting the dataset is organized into
a forest of ![]() trees, each of depth
trees, each of depth ![]() .
Here
.
Here ![]() may be viewed as depending on
may be viewed as depending on ![]() , the distance
function, and on the dataset. The radius of interest
, the distance
function, and on the dataset. The radius of interest ![]() is an input to the organization process and the result is a
linear space data structure specialized to answer queries
within this distance. Searches then require
is an input to the organization process and the result is a
linear space data structure specialized to answer queries
within this distance. Searches then require
![]() time, or
time, or ![]() time given
time given ![]() processors.
processors.
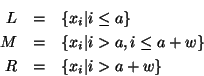





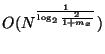 .
.