Up: Publication homepage
A Bipartite Matching Approach to
Approximate String Comparison and Search
Samuel R. Buss1
-
Peter N. Yianilos2
Abstract:
Approximate string comparison and search is an important part
of applications that range from natural language to the
interpretation of DNA. This paper presents a bipartite
weighted graph matching approach to these problems, based on
the authors' linear time matching algorithms
3. Our
approach's tolerance to permutation of symbols or blocks,
distinguishes it from the widely used edit distance and finite
state machine methods. A close relationship with the earlier
related `proximity comparison' method is established.
Under the linear cost model, a simple 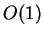 time per position
online algorithm is presented for comparing two strings given
a fixed alignment. Heuristics are given for
optimal alignment. In the approximate string search problem,
one string advances in a fixed direction relative to the other
with each time step. We introduce a new online algorithm for
this setting which dynamically maintains an optimal bipartite
weighted matching.
time per position
online algorithm is presented for comparing two strings given
a fixed alignment. Heuristics are given for
optimal alignment. In the approximate string search problem,
one string advances in a fixed direction relative to the other
with each time step. We introduce a new online algorithm for
this setting which dynamically maintains an optimal bipartite
weighted matching.
We discuss the application of our algorithms to natural
language text search, including prefilters to improve
efficiency, and the use of polygraphic symbols to improve search
quality. Our approach is used in the LIKEIT text search
utility now under development. Its overall design and
objectives are summarized.
Keywords:Approximate String Comparison,
Approximate String Search,
Text Search,
Sequence Comparison,
Bipartite Quasi-Convex Matching,
Distance Metric,
Natural Language Processing.
Search and the implied process of comparison, are fundamental notions
of both theoretical and applied computer science. The usual case is
that comparison is straightforward, and attention rests mainly
on search. Given finite strings over a finite alphabet 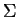 , one
might for example define comparison to be a test for equality, and the
well known dictionary problem arises. That is: organize a set of
strings for effective storage and retrieval of exact matches. Given a
short string
, one
might for example define comparison to be a test for equality, and the
well known dictionary problem arises. That is: organize a set of
strings for effective storage and retrieval of exact matches. Given a
short string  and a much longer one
and a much longer one  , one might also
strive to efficiently locate occurrences of
, one might also
strive to efficiently locate occurrences of  in
in  . This
is sometimes called the string matching problem [8].
. This
is sometimes called the string matching problem [8].
When the comparison method is generalized to allow inexact match, the
resulting ideas, algorithms, and data structures become somewhat more
complicated. Despite the added complexity, this research direction is
important because the resulting algorithms are frequently of greater
practical value. This is the case because almost all naturally
occurring strings are the result of a generative process which includes
error and ambiguity. Examples include natural language text, the
speech signal, naturally occurring DNA -- and just about any other
sequence which corresponds to measurement of a natural process.
Perhaps the most natural generalized comparison method relaxes the
requirement of exact equality to admit a bounded number of errors.
Each such error is typically restricted to be either an insertion,
deletion, substitution, or sometimes a transposition of adjacent
symbols. Given a query string, it is then possible to build a finite
state machine (FSM) to detect it, or any match within the error
bounds, within a second string. We will refer to this approach
generalizations of it as FSM methods.
The recent work of [10,12]
demonstrates that text can be scanned at very high speeds within
this framework for comparison.
Another well known approach to generalized string comparison computes
edit-distance (ED), which measures the least costly transformation
of one string into another using some set of primitive operations.
The most common choices of primitive operations
are insert, delete, substitute, and
sometimes adjacent transposition. A simple dynamic program computes
this distance in quadratic time, i.e. proportional to the product of
string lengths. See [11]
for a discussion of these and related
algorithms which we will refer to as ED methods.
Both the FSM and ED approaches rather strictly enforce temporal
ordering. In most applications this is to some extent desirable. We
observe however that similar strings from natural language exhibit
strong local temporal agreement but frequently include global ordering
violations. More concretely, words or entire clauses might be
rearranged with the result nevertheless ``similar'' to the original.
For example, the strings ``ABCD'' and ``DCBA'' are maximally distant
with respect to edit distance4. To transform the first into the
second, `A', `B', and `C' are first deleted, and then `C', `B', `A'
are inserted. This is not disturbing at the word level, but if each
symbol is replaced by a word, significant divergence from human
similarity judgment becomes apparent.
This paper presents a formal basis for string comparison and search
which is entirely distinct from both the FSM and ED paradigms. It
represents a computationally affordable solution to the problem of
preserving an emphasis on local temporal ordering, while allowing
global permutation. Our framework reduces string comparison to
multiple instances of the bipartite weighted matching problem, or as
it is sometimes called, the assignment problem. The bipartite graph's
two parts correspond to the strings being compared. The nodes are
symbols or, more generally, features present at each string position.
Edges connect symbols in one string with those in another and are
given costs which vary with the magnitude of positional
displacement. Local temporal ordering is emphasized by defining
features which consist of the polygrams of varying lengths found at
each string position. The overall solution is then superposition
of assignment problems for each distinct polygram. The sections
that follow describe our method in greater detail.
The ``proximity comparison'' method is a related approach used in
several commercial spelling error correctors and information retrieval
products. We show that this earlier method may be viewed as an
approximation to the assignment problem we solve exactly. Its
principal virtue is the algorithm's simplicity and resulting speed.
However proximity comparison requires two passes over the strings
being compared while we demonstrate that exact solution is possible
with only one. In both cases 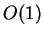 time is spent processing each
symbol. Thus the algorithms of this paper essentially supplant
the proximity comparison approach. Polygrams and other
context sensitive feature symbols
were used in proximity comparison based applications, but for practical
reasons, polygram length was generally limited to two. The ``Friendly Finder''
program5 is
an example of a proximity comparison based database retrieval system based entirely
on 1 and 2-grams and their positional relationship.
More recently Damashek and Huffman [5,6]
have developed a large scale text retrieval system based entirely on polygrams.
time is spent processing each
symbol. Thus the algorithms of this paper essentially supplant
the proximity comparison approach. Polygrams and other
context sensitive feature symbols
were used in proximity comparison based applications, but for practical
reasons, polygram length was generally limited to two. The ``Friendly Finder''
program5 is
an example of a proximity comparison based database retrieval system based entirely
on 1 and 2-grams and their positional relationship.
More recently Damashek and Huffman [5,6]
have developed a large scale text retrieval system based entirely on polygrams.
It is convenient to imagine two strings  and
and  arranged
on top of one another as in Figure 1. In this
example the graph's nodes consist of unigrams only, i.e., single
letters. In the `linear-cost' model the matching's cost is determined
by simply adding the horizontal displacements of each graph edge, and
imposing a penalty based on the number of unmatched nodes. It is
evident from the figure that a lower cost matching would result if
arranged
on top of one another as in Figure 1. In this
example the graph's nodes consist of unigrams only, i.e., single
letters. In the `linear-cost' model the matching's cost is determined
by simply adding the horizontal displacements of each graph edge, and
imposing a penalty based on the number of unmatched nodes. It is
evident from the figure that a lower cost matching would result if
 were shifted left by one position. This illustrates that the
cost of an optimal matching is a function of the string's relative
`alignment'. In some applications fixed alignment is assumed while
others require that alignment also be optimized. In the case of string
search, the long
were shifted left by one position. This illustrates that the
cost of an optimal matching is a function of the string's relative
`alignment'. In some applications fixed alignment is assumed while
others require that alignment also be optimized. In the case of string
search, the long  string is imagined to advance leftward with each
time step. Then problem then is to maintain an optimal matching
dynamically as time advances and the alignment changes. We'll describe
this problem in greater detail later and describe an algorithm which is
somewhat more efficient than the obvious solution which finds an entirely
new matching for each step.
string is imagined to advance leftward with each
time step. Then problem then is to maintain an optimal matching
dynamically as time advances and the alignment changes. We'll describe
this problem in greater detail later and describe an algorithm which is
somewhat more efficient than the obvious solution which finds an entirely
new matching for each step.
Figure 1:
String Comparison by Bipartite Weighted Matching
|
Figure 1 illustrates that each edge in the matching
connects identical symbols. Thus, for a given alignment, the overall
matching problem may be decomposed into a union of subproblems - one
for each alphabet member. We will show that each of these may be
further decomposed into `levels'. The level decomposition is
trivially produced in one-pass using what amounts to the ``parenthesis
nesting algorithm''. Finally, for each level, a simple one-pass
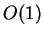 time per node algorithm finds the optimal matching. Since the
combined sizes of all subproblems equals the size of the original
problem, the original problem is solved in one-pass, using
time per node algorithm finds the optimal matching. Since the
combined sizes of all subproblems equals the size of the original
problem, the original problem is solved in one-pass, using 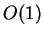 time
per symbol.
time
per symbol.
Finally we discuss the text search application and techniques which
improve processing speed and search quality. Polygraphic symbols of
variable length are employed at each node to increase the system's
sensitivity to local ordering changes. Before searching for the
optimal matching and alignment, several prefilter stages are employed
to effectively rule out most candidates. The LIKEIT system now
under development combines these techniques. In practice a database
record may be located given almost any query which remotely resembles
it. The system is character and polygram oriented and does not make
any effort to extract words from the query or the database. It is
perhaps best described as an approximate phrase retrieval system which
tolerates re-ordering while considering word proximity.
Bipartite Matching for String Comparison
We start with the mathematical definitions of strings, of bipartite
matchings and of the cost of a matching. In spite of the mathematical
abstraction of the definitions we present, the underlying idea is
quite simple; namely, given a query string  and a database string
and a database string  we wish to find an optimal one-to-one
assignment of symbols occurring in
we wish to find an optimal one-to-one
assignment of symbols occurring in  to occurrences of the same
symbols in
to occurrences of the same
symbols in  . Here `optimality' is measured in terms of the
distance from a symbol in
. Here `optimality' is measured in terms of the
distance from a symbol in  to its assigned symbol in
to its assigned symbol in  .
The `distance' corresponding to each such symbol assignment depends on
our choice of alignment for
.
The `distance' corresponding to each such symbol assignment depends on
our choice of alignment for  relative to
relative to  . For this
reason, our definition of a string will specify not just its contents,
but a position along the integer number line. The notion of an
optimal assignment is then well-defined since a position is implicit
in the definition of each string. Later we will consider a higher
level optimization problem, namely that of varying the relative
position (alignment) of the strings so as to optimize (minimize) the
assignment cost.
. For this
reason, our definition of a string will specify not just its contents,
but a position along the integer number line. The notion of an
optimal assignment is then well-defined since a position is implicit
in the definition of each string. Later we will consider a higher
level optimization problem, namely that of varying the relative
position (alignment) of the strings so as to optimize (minimize) the
assignment cost.
A string is intuitively a sequence of characters over a finite
alphabet 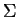 ; formally, a string
; formally, a string  has a domain
has a domain
![$[k,m] =
\{k,k+1,k+2,\ldots,m\}$](img9.gif) and is a mapping
and is a mapping
![$\alpha:[k,m]\rightarrow\Sigma$](img10.gif) . We denote by
. We denote by 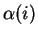 the symbol
at position
the symbol
at position 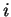 of
of  . Notice that only when a string's domain
is
. Notice that only when a string's domain
is ![$[1,m]$](img12.gif) is
is 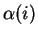 really the
really the 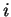 -th symbol. Allowing domains
more general than
-th symbol. Allowing domains
more general than ![$[1,m]$](img12.gif) makes it easier to describe the process of
searching for an optimal alignment, and the process of searching for
approximate occurrences of
makes it easier to describe the process of
searching for an optimal alignment, and the process of searching for
approximate occurrences of  in
in  .
.
Let  be a string with domain
be a string with domain ![$[k,m]$](img13.gif) .
If
.
If
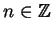 , then we
let
, then we
let
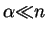 denote the string
denote the string  with domain
with domain
![$[k-n,m-n]$](img16.gif) such that
such that
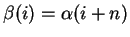 . The length,
. The length, 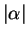 ,
of
,
of  is equal to
is equal to 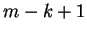 , the number of symbols in
, the number of symbols in  .
We use
.
We use
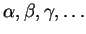 as meta-symbols for strings and
as meta-symbols for strings and
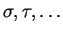 as meta-symbols for symbols from
as meta-symbols for symbols from 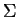 .
.
The two-sided cost is more useful
in the string comparison problem where one wants a notion
of the distance between  and
and  ; on the other hand, the
one-sided cost is more useful for the string search problem
where one wants to know to what extent
; on the other hand, the
one-sided cost is more useful for the string search problem
where one wants to know to what extent  is contained within
is contained within  .
Note that if
.
Note that if  and
and  are equal length, then the one-sided and
two-sided costs are identical.
are equal length, then the one-sided and
two-sided costs are identical.
The function
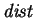 enjoys the property of being a metric:
enjoys the property of being a metric:
Theorem 1
Let the cost function
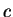
be non-decreasing and satisfy
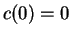
and
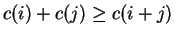
for all
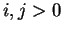
.
Then
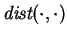
is a metric. That is,
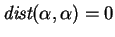
,
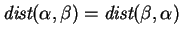
and
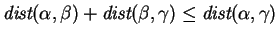
,
for all

,

and
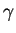
.
There are a large number of enhancements that can be made to the definitions
of cost and distance. For example, it is possible to assign every character a
real-valued weight and then weight the costs proportionally to the
weight of the character. It is also possible to more heavily weight
characters near the beginning of  , etc. These enhancements can be
very useful in practice to improve the perceived quality of the optimal
assignment; however, they make little difference to the algorithms described
in this paper, so we shall use just the simple notion of cost as defined
above.
, etc. These enhancements can be
very useful in practice to improve the perceived quality of the optimal
assignment; however, they make little difference to the algorithms described
in this paper, so we shall use just the simple notion of cost as defined
above.
In [4]
the authors have developed linear time and near-linear time algorithms
for finding minimum cost bipartite matchings when the cost function
is concave down. Although space does not permit us to review the
details of this algorithm, we shall review a few keys
aspects of the algorithm which are needed in the case when the cost
function is linear (i.e., when
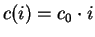 for some constant
for some constant 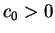 ).
).
For simplicity assume that  and
and  are both strings with
domain
are both strings with
domain ![$[1,n]$](img34.gif) .6Let
.6Let  be a symbol which occurs at position
be a symbol which occurs at position 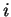 in
in  , i.e.,
, i.e.,
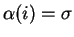 . Then
. Then
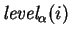 is equal to
the number of
is equal to
the number of  's that occur in
's that occur in ![$\alpha[i,i-1]$](img38.gif) minus the
number that occur
minus the
number that occur ![$\beta[1,i-1]$](img39.gif) . Similarly, if
. Similarly, if 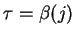 ,
then
,
then
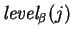 is equal to the number of
is equal to the number of 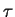 's in
's in ![$\alpha[1,i]$](img43.gif) minus the number in
minus the number in ![$\beta[1,i-1]$](img39.gif) minus 1. A simple, but important,
fact about optimal matchings is:
minus 1. A simple, but important,
fact about optimal matchings is:
Proposition 2
([
1, Lemma 1] or
[
4, Lemma 4])
Let
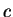
be concave down and
assume
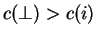
for all
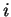
.
There is an optimal cost matching
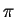
such that, for all
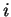
,
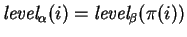
whenever
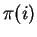
is
defined.
Proposition 2 provides the first step towards an algorithm
for finding
an optimal matching. This first step is to separately consider each
symbol  and to calculate the level of each occurrence of
and to calculate the level of each occurrence of  in both
in both  and
and  ; for each level
; for each level 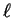 , we can separately
find an optimal matching on the
, we can separately
find an optimal matching on the  's at level
's at level 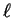 . Taking the
union of the these matchings
gives an optimal matching for
the original strings.
This allows us to reduce the problem of finding the optimal
bipartite matching between
. Taking the
union of the these matchings
gives an optimal matching for
the original strings.
This allows us to reduce the problem of finding the optimal
bipartite matching between  and
and  to the following
problem:
to the following
problem:
A complete solution to the alternating matching problem, and thereby
the matching problem, for concave-down cost functions was given by the
authors in [4].
A particularly simple, yet useful, special case of this is when
the cost function is linear. In this case, the following
theorem explains how the algorithm of
[4]
is simplified.
Part (a) is a simple special case of the well-known Skier and Skis
problem, see [7,9]. Part (b)
is the generalization to unbalanced matching.
In [4]
we proved that there is a linear time algorithm
to solve the alternating matching problem of Theorem 3 (since
a linear cost function clearly satisfies the weak crossover condition; the
algorithm, as explained there, made two passes over the words from left to right.
For the special case of a linear cost function, there is a much simpler online
algorithm which uses  time per symbol:
time per symbol:
Theorem 4
Let
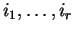
and
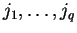
be an instance of the alternating matching problem and
assume w.l.o.g. that
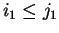
.
There is an online algorithm, which scans the values
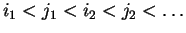
in
sequential order using constant time per value, which finds the optimal matching
described in Theorem
3.
The previous section considered the problem of finding the minimum
cost matching between two strings  and
and  ; will the
positions of the two strings were held fixed. Frequently, however, it
is desirable to allow the strings to be shifted relative to one
another to find a better matching. An example of this would be
matching the string
; will the
positions of the two strings were held fixed. Frequently, however, it
is desirable to allow the strings to be shifted relative to one
another to find a better matching. An example of this would be
matching the string 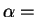 ``SOUR'' against
``SOUR'' against 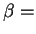 ``DINOSAUR''.
If the strings are aligned so that both
``DINOSAUR''.
If the strings are aligned so that both  has domain
has domain ![$[1,4]$](img68.gif) and
and  has domain
has domain ![$[1,8]$](img69.gif) , then the total cost will be
, then the total cost will be
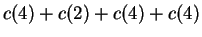 . However, by realigning the strings and
shifting
. However, by realigning the strings and
shifting  leftward by 4 (thereby letting it have domain
leftward by 4 (thereby letting it have domain
![$[-3,4]$](img71.gif) , the total cost is reduced to
, the total cost is reduced to
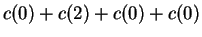 .
.
We call the problem of finding the optimal shift of  the realignment problem. We give below two heuristics for finding a good
realignment. The first, based on `center-of-gravity', is quick to
implement but does not always produce an optimal free realignment.
The second, based on a median calculation always produces an optimal
free realignment, but is more time-consuming to compute.
the realignment problem. We give below two heuristics for finding a good
realignment. The first, based on `center-of-gravity', is quick to
implement but does not always produce an optimal free realignment.
The second, based on a median calculation always produces an optimal
free realignment, but is more time-consuming to compute.
Let  and
and  be fixed strings; we define
be fixed strings; we define 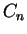 to equal
to equal
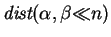 . The problem is find a
. The problem is find a 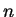 which
minimizes
which
minimizes 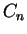 and to find a corresponding optimal cost
matching
and to find a corresponding optimal cost
matching  . The general idea is to iteratively calculate an
optimal match at a given alignment, then to calculate a ``free
realignment'' which improves the cost of the match, and then to repeat
the process. More formally, we define a free realignment as follows:
. The general idea is to iteratively calculate an
optimal match at a given alignment, then to calculate a ``free
realignment'' which improves the cost of the match, and then to repeat
the process. More formally, we define a free realignment as follows:
The general approach we take to realignment is based on the following
algorithm:
` =13`^M=13
Algorithm
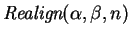 Set
Set 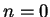 Loop
Set
Loop
Set 
 optimal matching of
optimal matching of  and
and
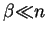 .
Let
.
Let
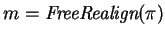 If
If 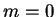 ,
Exit loop
Set
,
Exit loop
Set 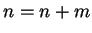 Endloop
Endloop
Here
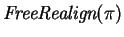 is a function that computes a free
realignment.
is a function that computes a free
realignment.
We suggest
two possible methods of computing
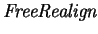 : the first is based on a
`center-of-gravity' calculation:
the center of gravity,
: the first is based on a
`center-of-gravity' calculation:
the center of gravity,
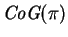 , of
, of 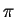 is defined to equal
is defined to equal
rounded to nearest integer.
Then one can use
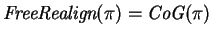 . The
. The
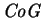 function
is easy to compute, is fast, and has worked well in the LIKEIT system
described in section 3.4. However, it is not guaranteed
to always yield the best possible free realignment: an example of
this is when the string
function
is easy to compute, is fast, and has worked well in the LIKEIT system
described in section 3.4. However, it is not guaranteed
to always yield the best possible free realignment: an example of
this is when the string  ``ABC'' is compared to the string
``ABC'' is compared to the string
 ``A - - - BC'' where the dashes represent a long string of blanks;
in this case, the
``A - - - BC'' where the dashes represent a long string of blanks;
in this case, the
 free realignment would reposition
free realignment would reposition  so that
so that
 is placed at the two-thirds mark of
is placed at the two-thirds mark of  . However, the optimal
free realignment, i.e., the one with minimum cost, would be to have the
end of
. However, the optimal
free realignment, i.e., the one with minimum cost, would be to have the
end of  positioned at the end of
positioned at the end of  so that the substrings ``BC''
are perfectly aligned.
so that the substrings ``BC''
are perfectly aligned.
Our second free realignment algorithm is based on the median value (rather than
the mean) of the differences 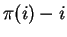 . The median
. The median 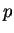 of
a multiset
of
a multiset 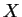 of integers is defined as usual; if
of integers is defined as usual; if 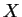 has an even number
of members, then there are two ``middle'' elements
has an even number
of members, then there are two ``middle'' elements 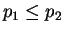 of
of 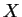 and
every
and
every 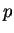 ,
,
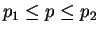 is considered to be a median value for
is considered to be a median value for 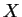 .
Let
.
Let
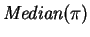 be defined to equal
the (i.e., any) median of
the multiset
be defined to equal
the (i.e., any) median of
the multiset
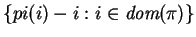 . Then the following theorem
shows that
. Then the following theorem
shows that
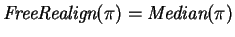 is an optimal free realignment.
is an optimal free realignment.
Theorem 5
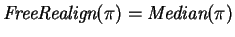
gives a minimum cost free realignment
of

and

under
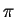
.
Unfortunately, although the use
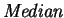 for free realignment always
provides an optimal free realignment, this does not mean that
for free realignment always
provides an optimal free realignment, this does not mean that
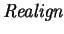 must converge to an alignment which is even locally
optimal. For example, suppose that
must converge to an alignment which is even locally
optimal. For example, suppose that 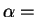 ``BCA'' with domain
``BCA'' with domain
![$[1,3]$](img99.gif) , that
, that 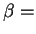 ``ACBXA'' with domain
``ACBXA'' with domain ![$[1,5]$](img100.gif) , that
, that 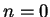 , and
that
, and
that 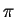 is the optimal matching for this alignment with
is the optimal matching for this alignment with 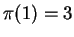 ,
,
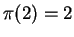 and
and 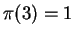 . The (only) median value for this
. The (only) median value for this 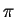 is
is
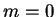 . However, the alignment is not locally optimal, since there is
a matching
. However, the alignment is not locally optimal, since there is
a matching 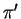 of
of  and
and
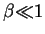 which has
lower cost, assuming
which has
lower cost, assuming
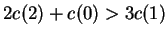 ; namely,
; namely,
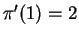 ,
,
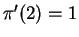 and
and
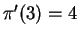 .
.
For this reason, the above realignment remains merely a useful
heuristic, which works well in practice, but may fail to produce an
optimal alignment in some rare situations. Both the
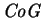 function
and the
function
and the
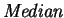 function are computable in linear time; but, in
practice, the
function are computable in linear time; but, in
practice, the
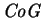 is slightly simpler and quicker to compute and seems to
yield very good results. Therefore, the
is slightly simpler and quicker to compute and seems to
yield very good results. Therefore, the
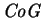 -based free
realignment is used in the prefilter stages of the LIKEIT system, while
the
-based free
realignment is used in the prefilter stages of the LIKEIT system, while
the
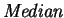 approach when computing the final matching.
approach when computing the final matching.
Our development above began by considering the problem of approximate
string comparison given a fixed alignment of the query string relative
to a database string. We then discussed optimization of this
alignment. But in both cases the setting was record oriented,
i.e., it was assumed that  and
and  are complete records
such as words, names, etc. In this section we consider the different
but related problem of approximate string search using our bipartite
matching outlook. Here, one of the two strings is generally much
longer, e.g., a paragraph or an article,
and represents the text to be searched. The shorter string is
thought of as the human generated query. The text is imagined to be
in motion passing by the query as depicted in
Figure 2.
are complete records
such as words, names, etc. In this section we consider the different
but related problem of approximate string search using our bipartite
matching outlook. Here, one of the two strings is generally much
longer, e.g., a paragraph or an article,
and represents the text to be searched. The shorter string is
thought of as the human generated query. The text is imagined to be
in motion passing by the query as depicted in
Figure 2.
Figure 2:
In Approximate String Search an optimal Bipartite
Weighted Matching is maintained within a fixed window as text
slides by a stationary query.
|
Our earlier record oriented approach could in principle be applied in
this setting but several problems exist. First, the local search
heuristics introduced cannot be relied upon to produce a global
optimum alignment, so one would be led to recompute the entire
matching for each alignment. Second, under the linear cost function,
the agreement between our mathematical notion of similarity, and human
judgment, appears to break down substantially. To see this consider
that varying the position of a distant matching symbol affects the
score just as much as nearby variations. If one is searching for
keywords without regard to their position, this may be reasonable
behavior. But if the query represents a phrase or collection of words
which are expected to occur in close proximity, then those parts of
the query which match only to distance locations, can easily dominate
the overall matching score. This in part motivated the authors to
consider non-linear quasi-convex cost functions in their earlier work.
The approach we take in this paper is to use linear costs, but
restrict the matching process to a moving window in the text indicated
with a dotted line in Figure 2. That is, matching
edges are allowed only within the window. For each position of the
text relative to the query, a different bipartite matching may exist.
The problem we face then consists of efficiently maintaining an
optimal matching as the text slides by.
As before, the problem separates immediately by alphabet symbol and we
may therefore focus on the subproblem corresponding to a single
symbol. We will again use the notion of a level decomposition but now
must from time to time adjust it as the text slides by. Focusing
on a single level, it is important to realize that the optimal
matching may itself change as the text moves; before the need arises
to recompute levels. We think of these two eventualities as events
for which an alarm is set sometime in the future, i.e. the events
consisting of the recomputation of levels, and of the optimal matching
for a level. Until one of these alarms sounds, it is easy to see that
each matching edge will grow either shorter or longer by one with each
time step. An edge will never change growth direction between alarms
because such a change would correspond to a releveling event. Hence
in-between alarms, the overall matching cost will change by a constant
amount per time step given by the total of each edge change.
The algorithms we describe work by computing for each symbol
subproblem, the cost of the optimal matching, the number of time steps
before an alarm event, and the change in matching cost per time step.
The cost changes for each symbol are summed to form a single value.
So until an alarm sounds for some symbol, processing a time step
consists of adding this single value to adjust the cost of the optimal
matching. A trivial outer loop manages the alarms and updates the
cost change variables.
In the worst case, alarms might sound on nearly every time step and
our algorithm is no better than the direct approach in which one
merely recomputes the optimal matching cost for at every time step.
But in some problem domains such as natural language text, the
alphabet may be defined so that considerable savings result. For
example one can define the alphabet to consist of, say, 2-grams or
3-grams but exclude 1-grams. Doing this makes the problem
considerable more sparse and many subproblems will sleep for
many time steps before any work is needed. So if 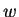 is the window's
size, our algorithms might perform
is the window's
size, our algorithms might perform 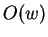 work per time step. One
might hope to find and algorithm with instead does
work per time step. One
might hope to find and algorithm with instead does 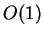 or
or 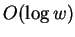 work per step, perhaps on an amortized basis. This represents an
interesting area for future work. Failing such a result, one might
analyze algorithms like the one we present under the assumption of
some distribution of strings.
work per step, perhaps on an amortized basis. This represents an
interesting area for future work. Failing such a result, one might
analyze algorithms like the one we present under the assumption of
some distribution of strings.
Since the outer level processing is rather straightforward, we confine
our discussion to the matching subproblem for a single symbol which we
will denote  . Our algorithm represents the occurrences of
. Our algorithm represents the occurrences of
 in
in  as a linked list which is formed before search
begins. The occurrences in
as a linked list which is formed before search
begins. The occurrences in  are also maintained as a linked
list but this list is sometimes updated. An entry is added to the
tail when
are also maintained as a linked
list but this list is sometimes updated. An entry is added to the
tail when  is shifted onto (becomes the) right-end of
is shifted onto (becomes the) right-end of  during a time step. The list's head is deleted when
during a time step. The list's head is deleted when  is
shifted out of the window. Assuming a constant number of symbols are
present at each string position the maintenance of these lists is
clearly
is
shifted out of the window. Assuming a constant number of symbols are
present at each string position the maintenance of these lists is
clearly 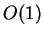 cost per step. No lists need to be formed for alphabet
symbols in
cost per step. No lists need to be formed for alphabet
symbols in  which do not occur in
which do not occur in  .
.
Time steps are denoted 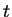 and numbered from zero. We denote by
and numbered from zero. We denote by 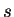 the offset of the windows right edge from the first position of
the offset of the windows right edge from the first position of
 . The list entries for
. The list entries for  consist of an integer giving
the time step during which the particular
consist of an integer giving
the time step during which the particular  occurrence was
shifted onto
occurrence was
shifted onto  . The list entries for
. The list entries for  consist of the
position of each
consist of the
position of each  occurrence in the natural coordinate system
in which the first position is zero. At each time step the
occurrence in the natural coordinate system
in which the first position is zero. At each time step the  lists are effectively renumbered by adding
lists are effectively renumbered by adding 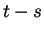 to each element before
it is used.
to each element before
it is used.
We will show that a single scan through the two lists associated with
 finds the optimal matching, its cost, and the two alarm
intervals corresponding to leveling and rematching as described above.
This scan is performed when an earlier alarm sounds, and also when
finds the optimal matching, its cost, and the two alarm
intervals corresponding to leveling and rematching as described above.
This scan is performed when an earlier alarm sounds, and also when
 either appears on the right, or vanishes from the left of the
window.
either appears on the right, or vanishes from the left of the
window.
The first part of the process consists of merging the two lists to
produce a single sorted list. During the merge it is a
straightforward matter to split the list into sublists, one for each
level. Also, during the merge, it is easy to set the leveling alarm
by focusing on positions in the merged list where a  list
element is immediately followed by an
list
element is immediately followed by an  list element. The
minimum gap between such pairs gives the value of the leveling alarm
and may be trivially maintained during the scan.7 We have seen in an
earlier section that the optimal matching and its cost may be found
for each level in an online fashion, so we have only to show that the
rematching alarm can be set as well.
list element. The
minimum gap between such pairs gives the value of the leveling alarm
and may be trivially maintained during the scan.7 We have seen in an
earlier section that the optimal matching and its cost may be found
for each level in an online fashion, so we have only to show that the
rematching alarm can be set as well.
Before turning to this we remark that an 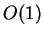 or
or 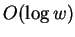 per
step algorithm will need to either leave leveling behind, or maintain
the levels using non-trivial data structures. To see this consider
that a block of say 10
per
step algorithm will need to either leave leveling behind, or maintain
the levels using non-trivial data structures. To see this consider
that a block of say 10  occurrence in
occurrence in  moving over a
block of 10
moving over a
block of 10  occurrences in
occurrences in  will generate a leveling
event at every time step. Moreover a quadratic number of matching
edge changes are generated despite the fact that the canonical skis
and skiers matching might have been used; avoiding all leveling alarms,
matching edge changes, and rematching alarms. This is of course only
true for examples like the one above in which the number of
will generate a leveling
event at every time step. Moreover a quadratic number of matching
edge changes are generated despite the fact that the canonical skis
and skiers matching might have been used; avoiding all leveling alarms,
matching edge changes, and rematching alarms. This is of course only
true for examples like the one above in which the number of  occurrence in
occurrence in  exactly equals the number in
exactly equals the number in  . Still
though it may provide intuition leading to an improved algorithm for
the general case.
. Still
though it may provide intuition leading to an improved algorithm for
the general case.
Figure 3:
The cost of leaving the 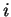 th element unmatched minus
the cost of leaving the last element unmatched, increases
by
th element unmatched minus
the cost of leaving the last element unmatched, increases
by 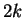 with each time step.
with each time step.
|
Focusing now on an individual level, recall that it must consist of
elements which alternate between  and
and  . If level is of
even length, then all elements are matched and no rematching is
required until the leveling itself changes. If the level is of odd
length, then exactly one element will be left unmatched in an optimal
matching. Since we are processing the level online, we don't know in
advance whether it is of odd or even length. But this poses no real
problem since we may assume that it is odd until we reach the end and
perhaps find out otherwise.
. If level is of
even length, then all elements are matched and no rematching is
required until the leveling itself changes. If the level is of odd
length, then exactly one element will be left unmatched in an optimal
matching. Since we are processing the level online, we don't know in
advance whether it is of odd or even length. But this poses no real
problem since we may assume that it is odd until we reach the end and
perhaps find out otherwise.
Assume without generality that the situation is as in
Figure 3, i.e. the level begins with a  element, that the level is of odd length, and that
element, that the level is of odd length, and that  contains
the unmatched element. Part (a) of this figure depicts the matching
in which element
contains
the unmatched element. Part (a) of this figure depicts the matching
in which element 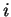 of
of  is left unmatched. Part (b) shows the
matching in which the last element is excluded. As
is left unmatched. Part (b) shows the
matching in which the last element is excluded. As  slides to
the left, the edges to the left of
slides to
the left, the edges to the left of 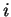 in both parts of the figure,
decrease in cost by
in both parts of the figure,
decrease in cost by 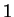 . However the
. However the 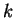 edges to the right of
edges to the right of 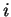 behave differently. In part (a) they grow more costly by
behave differently. In part (a) they grow more costly by 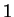 while in
(b) their cost declines by
while in
(b) their cost declines by 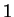 . So the difference between the cost of
these two matchings, i.e. that of part (a) minus that of part (b),
increases by
. So the difference between the cost of
these two matchings, i.e. that of part (a) minus that of part (b),
increases by 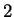 with each time step. Of course this is true only
until elements cross, but by that time a leveling alarm will
have sounded.
with each time step. Of course this is true only
until elements cross, but by that time a leveling alarm will
have sounded.
Figure 4:
Graph of the difference computed in Figure 3.
Minima correspond to optimal matchings, and as time passes
the 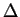 values increase at a rate which increases linearly
from right to left.
values increase at a rate which increases linearly
from right to left.
|
For each position 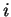 we denote this difference
we denote this difference 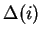 . The
optimal matching corresponds to a minimum of this function's graph. We
now imagine animating the graph with respect to time using the
. The
optimal matching corresponds to a minimum of this function's graph. We
now imagine animating the graph with respect to time using the 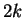 per step rule derived above. Each value
per step rule derived above. Each value 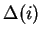 may be expanded
to become a function of time:
may be expanded
to become a function of time:
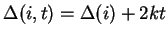 where
where
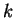 denotes the level's length minus
denotes the level's length minus 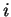 . It is apparent that the as
we move from left to right through a level, the rate of increase in
. It is apparent that the as
we move from left to right through a level, the rate of increase in
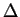 declines. This situation is illustrated in
Figure 4. So as time passes, the values of
declines. This situation is illustrated in
Figure 4. So as time passes, the values of 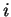 which represent minima will in general change. Notice that the the
absolute vertical location of this graph does not affect the
identification of an optimal matching since the minima are unchanged
by vertical translation. Also observe that the differences
which represent minima will in general change. Notice that the the
absolute vertical location of this graph does not affect the
identification of an optimal matching since the minima are unchanged
by vertical translation. Also observe that the differences
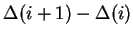 are easily computed online from local
differences within the level list. So up to vertical translation,
this graph may be built online starting from an arbitrary value and
accumulating
are easily computed online from local
differences within the level list. So up to vertical translation,
this graph may be built online starting from an arbitrary value and
accumulating
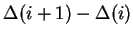 values.
values.
We will show that as the graph is built from left to right, we can
easily and in constant time update the value of variable alarm
which gives the number of time steps until the graph has a new global
minimum. This corresponds of course to a change in the optimal
matching and is the ``rematching'' alarm we require to complete our
algorithm for string search. Two observations are all that is needed
to understand the short algorithm that follows. First, if during
left to right graph construction, a new global minimum is encountered,
then no earlier point can ever replace it since all earlier points
are increasing in value at a greater rate. Second, if the current
point is greater than or equal to the current global minimum, then
the number of time steps that will pass before the current point
becomes smaller than the current global minimum, is exactly
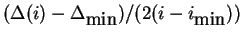 . The following
algorithm results:
. The following
algorithm results:
` =13`^M=13
Algorithm
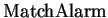 Set
Set
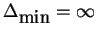 For
For
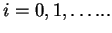 If
If
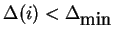 Set
Set
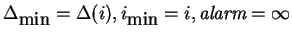 Else
Else
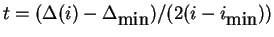 If
If
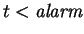 Set
Set
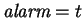
In this section, we give a new characterization of what we here call
the proximity metric on strings. This metric and various
generalizations, developed primarily by the second author,
has been reported in
[16,13,15,2]
and has been used extensively for natural language applications, especially
spelling correction,
by Proximity Technologies and a large number
of word processing software publishers, and by Franklin Electronic Publishers
in their hand-held solid-state electronic books. Other product implementations
include the PF474 VLSI circuit [14], the ``Friendly Finder'' database
retrieval system, the ``Proximity Scan'' subroutine library,
and the ``Clean Mail''
program for eliminating duplicates in mailing lists.
We are
proposing the bipartite graph matching approach
to string matching as
an improvement over the proximity metric for string matching.
The proximity metric has a fast, efficient implementation and has proven
to work well for many natural language applications. However, we argue
below that our new bipartite graph matching approach provides a qualitative
improvement over the proximity matching and, as we have already seen, the
bipartite graph based string matching can be performed efficiently in
linear time, so its performance rivals that of the proximity metrics.
Space does not allow a complete treatment of the proximity metric, but
we do include its full definition and proofs of the main new results.
For the rest of this section, we let  and
and  have equal
length and both have domain
have equal
length and both have domain ![$[1,n]$](img34.gif) .
.
It is clear that
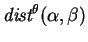 has value
has value 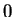 if
and only if
if
and only if 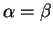 , and has value
, and has value 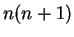 if and only if
if and only if
 and
and  have no common symbols. Traditionally, the
proximity metric has been a scaled version of
have no common symbols. Traditionally, the
proximity metric has been a scaled version of
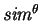 ;
namely,
;
namely,
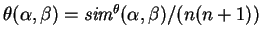 .
The next theorem is proved
in [13], and we omit its proof here:
.
The next theorem is proved
in [13], and we omit its proof here:
Theorem 6
Fix
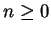
. Then
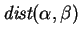
is a metric.
It has been known that
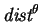 acts somewhat like
a matching-based string comparison method with linear cost function;
it also has been noted that the
acts somewhat like
a matching-based string comparison method with linear cost function;
it also has been noted that the
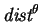 metric acts counter-intuitively
when there are unequal numbers of a given symbol in
metric acts counter-intuitively
when there are unequal numbers of a given symbol in  and
and  .
These phenomena are both explained by the following characterization
of
.
These phenomena are both explained by the following characterization
of
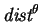 .
.
Before giving the characterization of
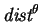 , we give a slightly
revamped definition of the
, we give a slightly
revamped definition of the
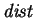 function; which is basically a
reformalization
of the discussion in section 2.1 where the algorithm finding an
optimal cost matching was implemented to first split symbols into
alternating tours at each level and then to find an optimal matching
for each tour independently.
We shall work with the cost function
function; which is basically a
reformalization
of the discussion in section 2.1 where the algorithm finding an
optimal cost matching was implemented to first split symbols into
alternating tours at each level and then to find an optimal matching
for each tour independently.
We shall work with the cost function 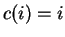 and
and
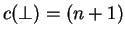 .
Let
.
Let
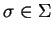 be a symbol and
be a symbol and
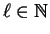 be a level number:
a
be a level number:
a 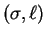 -matching
-matching 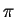 on
on  and
and  is a maximal
matching which maps (positions of) occurrences of
is a maximal
matching which maps (positions of) occurrences of  at
level
at
level 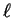 in
in  to
(positions of) occurrences of
to
(positions of) occurrences of  at
level
at
level 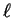 in
in  . (I.e.,
. (I.e., 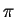 is injective
is either total or onto.)
The cost of such a
is injective
is either total or onto.)
The cost of such a 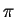 is equal to
is equal to
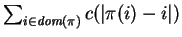 .
Recall that the level
.
Recall that the level 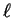 occurrences of
occurrences of  in
in  and
and  form an alternating tour and that Theorem 3
describes the ways in which minimum cost
form an alternating tour and that Theorem 3
describes the ways in which minimum cost 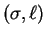 -matchings can be
formed. If case (a) of Theorem 3 holds, then
we say
-matchings can be
formed. If case (a) of Theorem 3 holds, then
we say  and
and  are
are 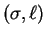 -balanced; otherwise,
there are unequal numbers of occurrences of
-balanced; otherwise,
there are unequal numbers of occurrences of  at level
at level 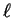 in
in
 and
and  and the strings
are said to be
and the strings
are said to be 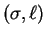 -unbalanced.
We define
-unbalanced.
We define
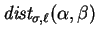 to be the minimum two-sided cost of
to be the minimum two-sided cost of
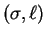 -matchings on
-matchings on  and
and  .
When there are no occurrences of
.
When there are no occurrences of  at level
at level 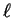 , then
, then
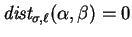 .
Proposition 2 tells us that the bipartite graph string
matching distance can be defined as
.
Proposition 2 tells us that the bipartite graph string
matching distance can be defined as
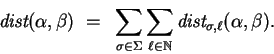
Now to give a similar characterization of
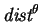 , let
, let
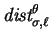 be defined by:
be defined by:
Note that in the case where  and
and  are
are 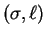 -unbalanced,
-unbalanced,
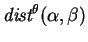 is just a constant, independent of the
positions of level
is just a constant, independent of the
positions of level 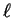 occurrences of
occurrences of  .
It may seem slightly
counterintuitive that the constant is
.
It may seem slightly
counterintuitive that the constant is 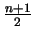 instead of
instead of 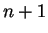 , since
if
, since
if  and
and  differ by exactly one character substitution then
differ by exactly one character substitution then
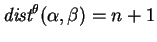 . However, in this case, there are
two values of
. However, in this case, there are
two values of 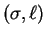 for which there is an unbalanced tour; one
for the character in
for which there is an unbalanced tour; one
for the character in  and one for the substituted character in
and one for the substituted character in  .
Each of there two unbalanced tours contributes
.
Each of there two unbalanced tours contributes 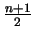 as
a
as
a
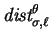 which is a net contribution of
which is a net contribution of 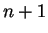 .8
.8
The string matching algorithms based on bipartite graph
matchings now are seen to present several advantages
over the proximity matchings. The principal two advantages are:
(1) The proximity matching approach is based on counting
common occurrences of symbol and does not give any assignment (i.e., matching)
of symbols in one string to symbols in the other string. The bipartite
graph approach to string matching does give such an assignment.
It can be potentially very useful to have such as assignment; firstly, since
it shows explicitly correspondences between the strings, and secondly since
the assignment can be used in a post-processing phase to further evaluate
the correspondence between the matched strings.
(2) The second advantage is the proximity matching seems to have serious
flaws when symbols do not occur equal numbers of times in both strings.
For an example consider the strings 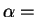 ``ABA'' and
``ABA'' and
 =``BAB'' and
=``BAB'' and 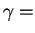 ``ABB''. Here we have
``ABB''. Here we have

(To normalize these distances to the range ![$[0,1]$](img161.gif) , they should be divided
by 12; e.g.,
, they should be divided
by 12; e.g.,
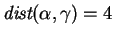 reflects the fact that
reflects the fact that
 and
and 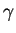 differ in exactly
differ in exactly 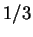 (
(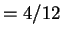 ) of their
symbols.) But now one clearly feels that
) of their
symbols.) But now one clearly feels that  is more similar to
is more similar to  than
than  is. Therefore, the fact that
is. Therefore, the fact that
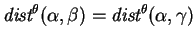 is undesirable, but
is undesirable, but
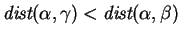 is as desired.
is as desired.
See the conclusion for a discussion of the relative merits of
the bipartite graph approach to string matching and of the
edit-distance (ED) approach to string matching.
In the bipartite approach to string matching discussed
above, a single string comparison is decomposed into
a linear superposition of matching problems; one for each alphabet
symbol. In this framework, even extensive permutation of a
string can result in a new string which is very close to the original,
as measured by the minimum cost of a matching between the new string
and the original string.
For natural language applications,
this behavior presents problems because perceptual distance increases
rapidly with local permutational rearrangement, while the cost of an
optimal matching does not. Fortunately, there is a simple way to augment
the string matching algorithm discussed above, to overcome these
problems; namely, to add additional polygraphic symbols to the strings
before performing the comparison.
The polygraphic symbols, called polygrams, consist of a sequence of
ordinary symbols. That is, a 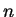 -gram, is a sequence of
-gram, is a sequence of 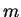 -symbols from
the underlying alphabet
-symbols from
the underlying alphabet 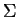 . Before comparing the strings
. Before comparing the strings  and
and
 , we preprocess them by adding, at each character position, new symbols
for the
, we preprocess them by adding, at each character position, new symbols
for the 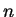 -grams which end at that position of the string. To give a concrete
example, LIKEIT system has used to the following method of preprocessing
a string
-grams which end at that position of the string. To give a concrete
example, LIKEIT system has used to the following method of preprocessing
a string  with domain
with domain ![$[1,m]$](img12.gif) : for each value
: for each value 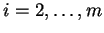 and
each
and
each 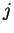 such that
such that
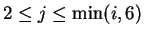 ,
let
,
let 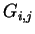 be the
be the 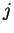 -gram comprising symbols
-gram comprising symbols
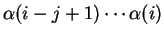 ;
then the polygrams
;
then the polygrams
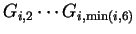 are inserted into
are inserted into  immediately following symbol
immediately following symbol 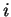 of
of  .
A similar
preprocessing is applied to
.
A similar
preprocessing is applied to  .
The number 6 has been chosen empirically
as it works well for natural language text applications.
For other applications,
e.g., DNA sequence analysis,
it might be more appropriate to use polygrams of different lengths.
.
The number 6 has been chosen empirically
as it works well for natural language text applications.
For other applications,
e.g., DNA sequence analysis,
it might be more appropriate to use polygrams of different lengths.
This preprocessing
makes  and
and  nearly six times as long, so one might fear
that it would increase the runtimes by a factor of six.
However, in practice, the
preprocessing
greatly improves the perceived quality of the matches and greatly reduces the
run time of the search process. The reason for the paradoxical
reduction of the runtime of the search
is that the prefilterings discussed in the next section, will
do a much more effective filtering thereby reducing greatly the number
of actual string comparisons which must be performed. Note that insertion
of polygraphic characters can be done efficiently,
by a finite state machine scanning from
left to right only.
nearly six times as long, so one might fear
that it would increase the runtimes by a factor of six.
However, in practice, the
preprocessing
greatly improves the perceived quality of the matches and greatly reduces the
run time of the search process. The reason for the paradoxical
reduction of the runtime of the search
is that the prefilterings discussed in the next section, will
do a much more effective filtering thereby reducing greatly the number
of actual string comparisons which must be performed. Note that insertion
of polygraphic characters can be done efficiently,
by a finite state machine scanning from
left to right only.
The LIKEIT system also gives different weights to polygrams than to
single symbols; namely, a 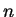 -gram receives a weight of
-gram receives a weight of 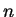 , so the
weight of a polygram is proportional to its length.
, so the
weight of a polygram is proportional to its length.
It should be noted that when polygrams are used, the optimal matching
may not respect overlapping polygrams. That is to say, even though two
polygrams overlap in  , they may be matched to widely divergent
polygrams in
, they may be matched to widely divergent
polygrams in  . As an example consider matching the strings
. As an example consider matching the strings
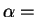 ``BART'' and
``BART'' and 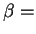 ``BARCHART''.
The initial 3-gram ``BAR'' in
``BARCHART''.
The initial 3-gram ``BAR'' in  would match the initial 3-gram of
would match the initial 3-gram of  ; whereas the overlapping
3-gram ``ART'' in
; whereas the overlapping
3-gram ``ART'' in  would match to the final 3-gram of
would match to the final 3-gram of  .
.
Polygrams are only one kind of extra symbols that can be inserted into
strings before
matching occurs. Other natural text search applications have used
the addition of symbols encoding phonetic information into the strings; in
this approach, phonetic information is inserted into both  and
and  using an algorithmic method (that is, the phonetic information is all inserted
algorithmically, there is no use of a dictionary).
using an algorithmic method (that is, the phonetic information is all inserted
algorithmically, there is no use of a dictionary).
Our matching approach may be thought of as a crude model for human
similarity judgment. Even though the corresponding are linear time
and very simple, it is in practice important to consider even simpler
models and algorithms in order to increase search speed. Perhaps the
simplest model consists of comparing the set of polygrams which occur
in both strings, along with their frequencies. That is, ignore
position entirely.
This may be thought of as a crude projection of the matching model so
as to use a cost function which assumes a constant value for all
matching edges independent of edge length. It corresponds to the use
of frequencies only in [5,6].
Other model simplifications involve approximations we have already
seen. Examples are the use of free realignment only, the
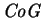 heuristic, and approximate solutions to each level's matching problem.
Another simplification consists of dealing fewer polygram sizes.
These simplified algorithms form prefilters which are applied to
the database in order to limit the search to a subset which is then
processed by later prefilters and ultimately by the final algorithm.
As records are considered by a prefilter, they are added to a heap of
bounded size. The next prefilter reads from this heap and writes to a
new one. For particular domains, transaction logs or query models may
be used to intelligently set the size of these heaps so that some
estimate of the probability of error (failing to pass-on the correct
record) is acceptable.
heuristic, and approximate solutions to each level's matching problem.
Another simplification consists of dealing fewer polygram sizes.
These simplified algorithms form prefilters which are applied to
the database in order to limit the search to a subset which is then
processed by later prefilters and ultimately by the final algorithm.
As records are considered by a prefilter, they are added to a heap of
bounded size. The next prefilter reads from this heap and writes to a
new one. For particular domains, transaction logs or query models may
be used to intelligently set the size of these heaps so that some
estimate of the probability of error (failing to pass-on the correct
record) is acceptable.
Our framework
allows for matching edges only between identical characters. This in some sense
corresponds to a discrete metric on 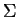 , i.e. a distance function assuming zero
only upon equality, and unity otherwise. In many languages this is awkward and in
some it may be an unacceptable simplification.
The simplest current practical technique
known to the authors consists of mapping each alphabet element to a string. The
mapping then attempts to capture linguistic relationships.
, i.e. a distance function assuming zero
only upon equality, and unity otherwise. In many languages this is awkward and in
some it may be an unacceptable simplification.
The simplest current practical technique
known to the authors consists of mapping each alphabet element to a string. The
mapping then attempts to capture linguistic relationships.
The LIKEIT Text Search Engine: Summary Preview
The ideas of this paper and the authors' earlier work have lead to the
development of LIKEIT; a new text search engine for the Web
[17]. The weighted matching approach
represents a single conceptual framework that deals with variations in
word spelling, form, spacing, ordering, and proximity within the text.
The system's objective is to provide an easy to administer, distributed
search service offering a great deal of error tolerance, and a very
simple user interface. The Web user's query is communicated to one or
more a LIKEIT search servers and an HTML document is
returned containing the most similar information found. The optimal
matching is visualized for the user by highlighting selected
characters in the returned text. Relationships between servers may be
established to form a distributed network search service which can
include explicit hierarchy when desired.
When a database of roughly 50,000 bibliographic citations is searched
for the query PROBLMOFOPTIMLDICTIONRY the title OPTIMAL
BOUNDS ON THE DICTIONARY PROBLEM is returned first. The search
requires a little over two seconds on a 133MHz Pentium processor based
system. In a more realistic example, a search for ``SAMBUSS''
finds papers by the first author as intended. Keyword-based
systems such as GLIMPSE and WAIS cannot by design. We remark that the algorithms of
this paper might then find application in construction of front-end
spelling correctors for keyword-based systems such as these.
There are several interesting directions for future work. Our
algorithms for approximate string search might be improved to provide
constant or nearly constant time bounds per time step. Strategies for
polygraphic indexing or hashing might be explored so that prefilters
can more rapidly limit the search's range. General techniques for
dealing with relationships between elements of 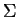 while
retaining computational efficiency might be developed. The alphabet
symbol weights and other parameters might be in some way learned by
the system. Finally, other application areas such as DNA analysis
might be explored.
while
retaining computational efficiency might be developed. The alphabet
symbol weights and other parameters might be in some way learned by
the system. Finally, other application areas such as DNA analysis
might be explored.
To conclude, we review again some of the relative advantages and disadvantages
between the bipartite graph string matching (BGSM) algorithms discussed in this
paper and prior edit distance (ED) algorithms. First, our BGSM algorithms
have the advantage of being online and taking linear time; in contrast,
ED algorithms are based on dynamic programming and require quadratic time
in general (but they can be made linear time if only a limited number of edit
operations
are allowed). The BGSM algorithms give a better quality match when the
strings being compared contain substantial differences; whereas the
ED approach gives a higher quality matching when the two strings
differ by only a few
edit operations (e.g., three or fewer). This is primarily due to the fact that
the BGSM algorithms match distinct alphabet symbols independently.
However, with use of polygraphic symbols, this disadvantage of the
BGSM algorithms can be largely overcome.
The ED distance algorithms have been widely used in text search
applications. A precursor to the BGSM algorithms, the proximity
matching, has also been widely used.
The BGSM algorithm provides a qualitative improvement over the
proximity matching; and is being deployed as a general
purpose tool in the LIKEIT text
search package.
- 1
-
A. AGGARWAL, A. BAR-NOY, S. KHULLER, D. KRAVETS, AND B. SCHIEBER, Efficient minimum cost matching using quadrangle inequality, in Proceedings
of the 33th Annual IEEE Symposium on Foundations of Computer Science, IEEE
Computer Society, 1992, pp. 583-592.
- 2
-
S. R. BUSS, Neighborhood metrics on n-dimensional blocks of
characters, Tech. Rep. 00218-86, Mathematical Sciences Research Institute,
Berkeley, September 1985.
- 3
-
S. R. BUSS, K. G. KANZELBERGER, D. ROBINSON, AND P. N. YIANILOS, Solving the minimum-cost matching problem for quasi-convex tours: An
efficient ANSI C implementation, Tech. Rep. CS94-370, U.C. San Diego,
1994.
- 4
-
S. R. BUSS AND P. N. YIANILOS, Linear and
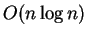 time
minimum-cost matching algorithms for quasi-convex tours.
time
minimum-cost matching algorithms for quasi-convex tours.
To appear in Siam J. Comput.. An extended abstract of this
paper appeared in Proceedings of the 5th Annual ACM-SIAM Symposium
on Discrete Algorithms, 1994, pp. 65-76., 199?
- 5
-
M. DAMASHEK, Gauging similarity with
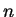 -grams: Language-independent
categorization of text, Science, 267 (1995), pp. 843-848.
-grams: Language-independent
categorization of text, Science, 267 (1995), pp. 843-848.
- 6
-
S. HUFFMAN AND M. DAMASHEK, Acquaintance: A novel vector-space
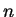 -gram technique for document categorization, in Proceedings, Text
REtrieval Conference (TREC-3), Washington, D.C., 1995, NIST, pp. 305-310.
-gram technique for document categorization, in Proceedings, Text
REtrieval Conference (TREC-3), Washington, D.C., 1995, NIST, pp. 305-310.
- 7
-
R. M. KARP AND S.-Y. R. LI, Two special cases of the assignment
problem, Discrete Mathematics, 13 (1975), pp. 129-142.
- 8
-
D. E. KNUTH, J. JAMES H. MORRIS, AND V. R. PRATT, Fast pattern
matching in strings, SIAM Journal on Computing, 6 (1977), pp. 323-350.
- 9
-
E. LAWLER, Combinatorial Optimization: Networks and Matroids, Holt,
Rinehart and Winston, 1976.
- 10
-
U. MANBER AND S. WU, GLIMPSE: A tool to search through entire file
systems, in Proceedings of the Winter 1994 USENIX Conference, 1994,
pp. 23-32.
- 11
-
D. SANKOFF AND J. B. KRUSKAL, Time Warps, String Edits and
Macromolecules: The Theory and Practice of Sequence Comparison,
Addison-Wesley, 1983.
- 12
-
S. WU AND U. MANBER, Fast test searching allowing errors,
Communications of the ACM, 35 (1993), pp. 83-91.
- 13
-
P. N. YIANILOS, The definition, computation and application of
symbol string similarity functions, Master's thesis, Emory University, 1978.
- 14
-
height 2pt depth -1.6pt width 23pt, A dedicated
comparator matches symbol strings fast and intelligently, Electronics
Magazine, (1983).
- 15
-
P. N. YIANILOS AND S. R. BUSS, Associative memory circuit system and
method, continuation-in-part.
U.S. Patent #4490811, December 1984.
- 16
-
P. N. YIANILOS, R. A. HARBORT, AND S. R. BUSS, The application of a
pattern matching algorithm to searching medical record text, in IEEE
Symposium on Computer Applications in Medical Care, 1978, pp. 308-313.
- 17
-
P. N. YIANILOS AND K. G. KANZELBERGER, The LikeIt distributed
Web search system.
Manuscript, in preparation, 1995.
A Bipartite Matching Approach to
Approximate String Comparison and Search
This document was generated using the
LaTeX2HTML translator Version 2K.1beta (1.47)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -image_type gif -nonext_page_in_navigation -noprevious_page_in_navigation -up_url ../main.html -up_title 'Publication homepage' -numbered_footnotes string_compare.tex
The translation was initiated by Peter N. Yianilos on 2002-06-30
Footnotes
- ... Buss1
- Supported in part by NSF grant DMS-9503247.
Department of Mathematics,
University of California, San Diego,
La Jolla, CA 92093-0112. Email: sbuss@ucsd.edu.
- ... Yianilos2
-
NEC Research Institute,
4 Independence Way, Princeton, NJ 08540 and
Department of Computer Science, Princeton University, Princeton, NJ 08544.
Email: pny@research.nj.nec.com.
- ... algorithms3
- Earlier
related works
[4,3]
of the authors may be obtained by anonymous ftp from euclid.ucsd.edu, directory pub/sbuss/research, filenames quasiconvex.ps and quasiconvex.Ccode.ps.
- ... distance4
- We assume only insertion and
deletion operators for simplicity
- ...
program5
- First published in 1987 by Proximity Technology Inc.
- ....6
- This simplifying assumption holds
without any loss of generality, since we can always pad strings with
new symbols which do not occur in the other string, so the strings
then have the same domain. Then a common shifting makes both strings begin
with position 1.
- ... scan.7
- During the
merge ties are broken in favor of
 .
.
- ....8
-
Another way to think about why
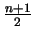 is used, is that
is used, is that
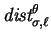 is intended to be a variation of a two-sided
cost.
is intended to be a variation of a two-sided
cost.
Up: Publication homepage
Peter N. Yianilos
2002-06-30
![]() time per position
online algorithm is presented for comparing two strings given
a fixed alignment. Heuristics are given for
optimal alignment. In the approximate string search problem,
one string advances in a fixed direction relative to the other
with each time step. We introduce a new online algorithm for
this setting which dynamically maintains an optimal bipartite
weighted matching.
time per position
online algorithm is presented for comparing two strings given
a fixed alignment. Heuristics are given for
optimal alignment. In the approximate string search problem,
one string advances in a fixed direction relative to the other
with each time step. We introduce a new online algorithm for
this setting which dynamically maintains an optimal bipartite
weighted matching.

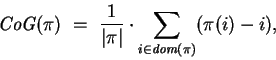

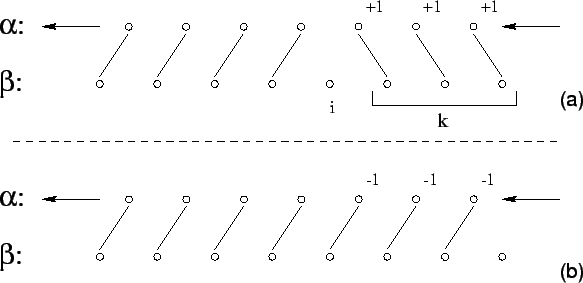
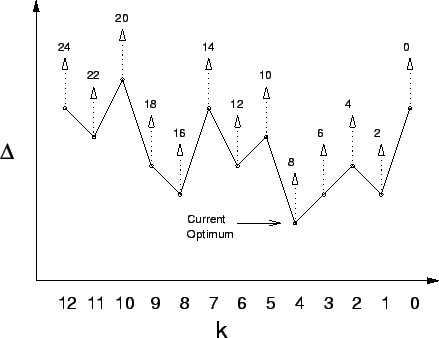
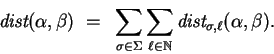
![\begin{displaymath}
{\mbox{\it dist}}^\theta_{\sigma,\ell} ~ = ~ \left\{\begin{a...
... [1ex]
\frac{n+1}{2} & \mbox{\rm otherwise}
\end{array}\right.
\end{displaymath}](img153.gif)
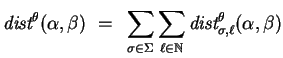 .
.