Secure Short-Key Cryptosystems:
Forty Bits is Enough

Samuel R. Buss ¹
Department of Mathematics
Univ. of Calif., San Diego -
Peter N. Yianilos ²
NEC Research Institute
Princeton, N.J.

June 1999

Abstract:

This paper discusses the use of short secret keys, as short as 40 bits or fewer, to implement secure public and private key cryptosystems. Short keys are readily memorized and do not need to be written down or stored electronically. Still, they can provide security comparable to that provided by conventional cryptosystems with much longer keys.

Our short secret key cryptosystems are based the use of slowed down key generation, as advocated by Quisquater, et al. We use a ``slow one-way'' function to convert a short secret key into an expanded key, which can be used in a conventional (long key) cryptosystem. Although the notion of slowdown in cryptographic systems is well-known, our analysis suggests that it is far more useful than is generally recognized.

The first contribution of this paper is the analysis of the security of short key cryptosystems and the tradeoffs between key length, amount of slowdown, and security. An important aspect of our analysis is the identification of the advantages of extremely slow slowdown functions for key generation. The second contribution is the inclusion of an auxiliary, nonsecret key; which we argue is necessary to maintain security, and also allows a single short key to be used for multiple independently secure communication sessions, and to be used as a master key in key management protocols.

Keywords: Cryptography, short secret key, slow one-way functions, security, key management.

Introduction

There are a wide variety of key-based cryptosystems which allow secret communication based on the use of keys which control encryption and decryption algorithms. In symmetric key systems, two parties share a common secret key and use common encryption and decryption methods. In public key cryptosystems, one party holds a secret key and the other party holds a public key (and often another set of secret/public keys are used dually in conjunction).³

The length of the secret key is an important parameter of a cryptosystem which affects the security of the cryptosystem. In order to have good security in practical symmetric key systems the secret key is typically of length 90 bits or longer; in public key systems, the secret key may need to be 1000 bits or longer for good security. This paper discusses a method for using short secret keys, of length approximately 40 bits, which achieve security equivalent to the security of conventional (long key) cryptosystems. Our short key cryptosystems can be used as either symmetric cryptosystems or as public key cryptosystems.

Perhaps the main advantage of the short key cryptosystem lies in key management. It is well-known that users have trouble remembering secret keys without writing them down; for 1000 bit keys, it more-or-less necessary to store the key electronically since such a long key can not be reliably typed in repeatedly. However, the 40 bit key of our short key cryptosystem is much easier to remember: this means that many key management issues can be avoided by the simple expedient of the user memorizing his or her key. This means that the short key cryptosystems are more secure against attacks which electronically access the user's computers and against attacks involving physical access or theft.

It is generally believed that a secret key must be sufficiently large in order to prevent attacks which exhaustively search the key space. In addition, one must assume that an adversary carrying out an exhaustive key search attack may construct special purpose hardware to test putative keys. In addition, the adversary may be able to test many keys simultaneously in parallel, either with the use of parallel computers or by distributing the workload to many computers across networks. A typical assumption is that $10^6$ keys per second can be considered by a single processor and at this rate a 40 bit key may be found in roughly ten days. However, with the use of special purpose hardware it is possible to check far more than $10^6$ keys second: Blaze et al.[3] suggest that RC4 keys could be checked at the rate of $3\times 10^7$ keys per second with FPGA's and at the rate of $8\times 10^8$ keys per second with custom VLSI chips. For parallel attacks, using multiple machines, even the estimate of $10^9$ keys per second would be deemed too low. For instance, as this paper was being written in mid-1998, it was reported that the EFF DES Cracker machine was capable of testing almost $5\times 10^{10}$ DES keys per second, using an array of 1500 custom VLSI chips. Thus it would seem necessary to use keys which are considerably longer than 40 bits to implement a secure system (see the discussion in [3]). This is unfortunate because short keys have the advantage that a person can easily remember them.

However, as is well-known (see [9,10]) exhaustion attacks are proportionally slowed down by increasing the time needed to test a single key. Quisquater, Desmedt, and Davio [9] were the first to suggest that a key generation scheme might be purposefully slowed down to thwart exhaustive key search attacks. Following their idea, we investigate the advantages of short key cryptosystems based on the idea of slow key expansion. The slow key expansion inserts a long delay into the time needed to test a putative key; thereby rendering it impossible to check millions or even thousands of keys per second. We extend the work of Quisquater et al. in two ways. First, we identify the necessity of an auxiliary nonsecret key both to prevent table-driven attacks and to allow a single short key to be used for multiple independently secure communication sessions. Second, we discuss the security of particular protocols based on short keys, and analyze the tradeoffs between key length, slowdown, and security; in particular we propose the use of extremely slow one-way functions. We also discuss the hardness properties that the slowdown function must satisfy. The result is secure cryptosystems with keys of length only 40 bits (the exact key length could be either shorter than or longer than 40 bits depending on the needs of the cryptosystem).

One of our motivations for this paper is that despite the straightforward nature of the slowdown technique used to create short key cryptosystems, its utility does not seem to be widely appreciated (see, for example, [3], which has an extensive discussion of exhaustive key search attacks, but does not mention slow-down methods).

A short key cryptosystem is built in tandem with a conventional symmetric key cryptosystem or a conventional public key cryptosystem. In our proposal, a secure cryptosystem is controlled by a short secret key, which can be expanded into an expanded key by use of a slow one-way function. A slow one-way function is a function which can be computed only with a certain delay and such that the inverse of the function cannot be feasibly computed. The expanded keys then play the role of the secret keys in the traditional symmetric key and public key systems. In addition, in order to substantially enhance security as well as to greatly increase the flexibility of the short key cryptosystem protocol, we augment the short secret key with an public auxiliary key. The auxiliary key is publicly known: it may be chosen at random or may contain identifying information. The expanded key will depend on both the private key and the auxiliary key and thus multiple expanded keys may be generated from a single secret key; this allows the same secret key to used for an extended time, even in multiple, independently secure, communication channels. In this way, a short secret key can be used as a master key in key management protocols of type proposed by [6,7].

The fact that the time required to test a potential secret key is important for the security of a cryptosystem is certainly well-known: the best example is the use of a 3-5 second delay in the Unix login protocol when an incorrect userid/password combination is presented. Quisquater et al. [9] proposed a slowdown in key generation for DES. A number of other authors have suggested the use of purposely slow-to-compute functions, similar in spirit to our slow functions but for other applications. These include [4] for designing uncheatable benchmarks, [5] for combating junk mail, [11] for ``timed-release'' cryptography and [2,1] for partial key escrow. The package transform of [10] is another approach to slowing down exhaustive key search, but only applies when very long messages are being sent. Our use of an auxiliary key is similar to the `salt' used with Unix passwords, to prevent table based attacks; auxiliary keys have also been used for theoretical constructions such as the the amplification of weak one-way permutations into one-way permutations. In spite of the prior usages of slowdowns, the effectiveness of purposeful slowdowns for key generation has not been recognized; for instance, the paper [3] discusses the need for long keys for security, without ever considering the use of slowdown functions. The current work is novel firstly in that we propose the use of very slow functions, with runtime from a few seconds up to several hours or even longer, as a crucial ingredient in preserving the security of cryptosystem. Secondly, the level of security which can be achieved is surprisingly high (see the tables for section 3.3). Thirdly, with the auxiliary keys, this allows short secret keys to serve as master keys in a key management protocol.

Section 2 of this paper describes the mathematical framework for the short key cryptosystems and defines the relationships between the short secret key, the public auxiliary keys and the expanded keys. Section 3 proposes several scenarios for the use of short key cryptosystems, illustrating their use in secure communication protocols. This includes estimates on timing, on level of security, on the overhead of computing expanded keys, etc. In addition, it describes how a single secret key may be used securely as the basis for multiple expanded keys for public key cryptography. In section 4, we suggest candidates for slow one-way functions.

The fact that we focus on 40 bit secret keys is somewhat arbitrary. Indeed for certain applications, even shorter keys will be adequate but there is a tradeoff with the slowness of the slow one-way function. For other applications, where stronger security is required or less slowness can be tolerated, one may wish to use short keys which are slightly longer than 40 bits. Finally, the length 40 bits is commonly regarded as the length permitted by the U.S. government for export purposes; however, this is not a real reason to consider 40 bit keys, both because we expect future changes in cryptography laws and because under current law the 40 bit limit would not necessarily apply to short key cryptographic protocols.

Short Keys and Slow Expansion

A short key cryptosystem consists of

(1)

a short key $K$ of length $\ell$ bits, $\ell=40$ for instance;

(2)

a slow one-way function $f$;

(3)

a conventional (long key) cryptosystem $C$. The system $C$ may be any symmetric or private key system, and it must use keys of sufficient length to be secure;

(4)

and usually auxiliary keys which are publicly known keys of $p$ bits in length.

The slow one-way function $f$ requires some explanation. Recall that a one-way function is a function $g$ so that $g(z)$ is easy to compute (in polynomial time, say), but such that $g$ is hard to invert; i.e., given a value $w$ of $g$, it is hard to compute a value $z$ such that $g(z)=w$. We further define a function $f$ to be slow if there is a known best runtime function $t=t(n)$ so that on inputs of length $n$, $f(z)$ can be computed in time $t(n)$, but cannot be computed in time substantially less than $t(n)$. Furthermore, we require that if $p$ distinct values $z_i$ are given, then any sequential machine which computes (even most of) the values of $f(z_i)$ should require time approximately equal to $p\cdot t(n)$; in other words, computing multiple values of $f$ simultaneously is no easier than computing the values independently. A slow one-way function is a function which is both slow and one-way. Generally, if one has a slow function $f^\prime$, and one can obtain a slow one-way function by composing $f$ with a one-way permutation.

In section 4 below, we shall and shall propose some candidates for slow one-way functions. For the moment, we just remark that the existence of slow one-way functions is not entirely obvious. In any event, until problems such as the P vs NP problem are solved, we will be unable to prove the existence of one-way functions. (It is at present the case that no conventional cryptographic system has been proved to be mathematically secure; our short key cryptosystems are no different in this regard.)

The basic protocol for short key cryptosystems is as follows. Two entities, Alice and Bob, wish to communicate securely. If the underlying conventional cryptosystem $C$ is a symmetric key system, then Alice and Bob share knowledge of $K$. On the other hand, for $C$ a public key system then only one (Alice, say) knows the secret key $K$. Alice, possibly jointly with Bob, chooses an auxiliary key, which we denote by $P$. The auxiliary key $P$ may be publicly known, and thus no secure communication is needed for its choice. Both $K$ and $P$ are input to the slow one-way function $f$ yielding the value $E=f(K,P)$. This value $E$ is called the expanded key and must have sufficient length to be used as a key for the conventional cryptosystem $C$, which is assumed to be secure against direct attacks on the conventional cryptosystem for that key length. Alice then uses the expanded key $E$ as the secret key for the system $C$ to communicate with Bob.

For $C$ a symmetric cryptosystem, Alice and Bob each have knowledge of the secret key $K$, which must be exchanged securely only once. The auxiliary key $P$ can be computed publicly and even changed repeatedly. Since Bob knows both $K$ and $P$, he uses $f$ to compute $E=f(K,P)$ and then, with knowledge of $E$, Alice and Bob communicate using $E$ as the secret key for the symmetric key system $C$.

For $C$ a public key system, Alice merely uses $E$ to generate her private and public keys $K_C^{priv}$ and $K_{C}^{pub}$ for the system $C$. As usual she keeps her private key $K_C^{priv}$ secret and she sends her public key $K_C^{pub}$ to Bob via a non-secure channel, but it is unnecessary for her to publicize her auxiliary key $P$. However, Alice does not need to save her long private key permanently, since she can always re-create it from $K$ and $P$ using $f$.

To give a brief estimate of the security of the short key cryptosystem, assume that an attacker knows the auxiliary key $P$ and has intercepted Alice's communication to Bob and is attempting a brute force attack by trying every possible 40-bit secret key. Further suppose that the computation of $f(K,P)$ requires time 1 second on a single computer and that the attacker uses 10000 computers in parallel to compute $f(K,P)$ for various values of $K$. Since $2^{40}/1000 \approx 10^9$, it will take the attacker approximately $10^9~\hbox{seconds} \approx 34.87~\hbox{years}$ to try all possible secret keys $K$. This allows for a substantial level of security! If more security is needed, one can easily choose a slower slow one-way function $f$. If less security is needed, one can use keys shorter than 40 bits.

An important role of the auxiliary key $P$ is to prevent a table-based attack. That is, without the use of $P$, the expanded key $E$ would depend only on $K$ and an attacker could build a table giving the expanded key corresponding to each value of $K$. For 40 bit keys, this table would contain $10^{12}$ keys, which is certainly not too large to store with today's memory technologies. The computation effort to compute this table would be immense, but perhaps not prohibitive, since the payoff would be large, namely, the table would allow a wide variety of messages to be almost immediately decoded. However, with the use of the public key $P$, this table-based attack is completely thwarted since the public key should be at least as long as the secret key and thus the table would be impossibly large.

Another role of the auxiliary key is to allow a single short key to be used as a master key in key generation protocols, see section 3.2. We discuss in more detail various short key cryptosystems protocols and their security in the next section.

Scenarios for Short Key Cryptography

The usefulness of 40 bit keys

One of the primary reasons that short key cryptography is useful is that is greatly simplifies key management and key security. The primary reason for this is that, as will be seen from the protocols below, that the secret key $K$ may be merely memorized without any need to write it down or store it electronically. The auxiliary keys may be longer and need to stored in writing or electronically, but they are publicly known anyway, and there is no need to keep the auxiliary keys secret.

There are several traditional ways in which the short keys might be memorized. The most straightforward way would be to use alphanumeric characters to encode the key. For instance, if a key consists of a string of symbols from a 36 symbol alphabet (uppercase letters and digits), then an eight symbol string encodes a secret key of just over 41 bits, while a seven symbol string encodes a secret key of just over 36 bits.⁴

A second possibility is to use a generalization of a method widely used by online internet service providers for user passwords. Namely, choose a set of approximately 10,322 well-known, distinct English words. Choosing three of these words at random, e.g., ``berm-aquatic-happy'' or ``seismic-shelf-lip'', encodes a secret key of 40 binary bits since $(10322)^3>2^{40}$. Of course, the words need to be chosen truly at random, unlike the two examples given here.⁵Using three English words to encode a key has the effect of making the key much easier to remember since mnemonic methods are more readily usable for key memorization.

For slightly longer keys, one could use four English words instead of three English words: this would give a secret key of 53 bits.

Suggested short secret key protocols

We first consider short key cryptographic protocols in which the underlying conventional long key cryptosystem $C$ is a symmetric key system. In this case, Alice and Bob begin by picking a short key $K$ of length $\ell$ bits. Later, when they wish to carry out a private communication, they jointly choose an auxiliary key $P$: this could be done by picking it at random, or by one them picking the auxiliary key unilaterally, or by having Alice and Bob each choose half the key at random if they fear the other has been subverted by an adversary. They then both compute $E=f(K,P)$, which takes time $t$. The expanded key $E$ is used as the key for the cryptosystem $C$ for their communications. Once they are done with the round of communication, they may erase the key $E$: if they later need to recover $E$, they can do so by recomputing $f(K,P)$.

One feature of the above protocol is that it is possible to use multiple auxiliary keys $P_i$, each one yields a key (presumably generally distinct) expanded key $E_i = f(K,P_i)$. Thus each communication session can use a distinct expanded key $E_i$. If any of the keys $E_i$ are compromised or revealed, then the rest of the communication sessions remain securely private, because of the one-way-ness of $f$.⁶

As a speculative application, the ability to use distinct expanded keys for different communication sessions would allow an business or an embassy to have a secured, shielded system that is used once per day, say, to generate a new expanded key $E_i$. The expanded keys would be used for a limited period of time and then erased.

Like any symmetric key cryptosystem, short key cryptosystems can also be used for user authentication. For this application, we envision a battery-powered, electromagnetically shielded, hand-held device which computes the function $f$. If a user, Alice, is remotely contacting Bob, then Bob may send a randomly chosen auxiliary key $P$. Alice enters first $P$ and then her short secret key $K$ into the hand-held device. After 10 seconds (for instance), the hand-held device displays the value $f(K,P)$. Alice then returns that value to Bob: Bob also knows $K$ and separately computes $f(K,P)$, comparing it to Alice's response. If they match, then Alice is authenticated. For this application to benefit from the use of the short key, it needs to be designed so that the value of $K$ and all intermediate memory values used in the computation of $f$ are thoroughly erased after the computation. In this case, theft of the hand-held device cannot compromise the secret key $K$.

Now we consider the protocols for the situation where the underlying conventional, long key cryptosystem $C$ is a public key system. If Alice wants to generate a public/private key pair for communication with Bob, she generates an auxiliary key $P$ (chosen randomly, say) and then computes $K_C^{priv} = E = f(K,P)$, which is her private key for use with the cryptosystem $C$. From this she computes the public key $K_C^{pub}$ which corresponds to $K_C^{priv}$ and sends $K_C^{pub}$ to Bob on an (insecure) channel.⁷ Note that Alice does not need to reveal her auxiliary key to Bob; on the other hand, if $P$ is revealed, then there is no loss of security. Once Alice and Bob complete a communication, Alice may erase her copies of $K_C^{priv}$; if she needs to recover it later she can recompute it from $E$ and $P$. This gives Alice the ability to recover old messages and to prove the content of old messages, without the security risk of keeping a long (1000 bits or more) private key in writing or electronically stored.

By varying the auxiliary key $P$, Alice can use a single short key to generate a large number of private/public key pairs for the cryptosystem $P$. In this way, Alice can have a large number of secure communications based on a single short secret key.

Since public key cryptosystems are quite flexible and allow many operations such as message signatures, message undeniability, message authentication, etc., all of the capabilities can be achieved with a short key cryptosystem.

Analysis of security

In designing a short key cryptosystem to have adequate security, the two most important parameters which can be varied are (a) the secret key length and (b) slowness of the slow one-way function $f$. These parameters should be chosen so as to keep the key length short, and so as to keep the slowness of $f$ being a serious impediment. In choosing the parameters, one should consider how large an attack may be mounted, how certain one is about the slowness of $f$, and how often the slow function $f$ must be computed.

We let $\ell$ denote the length of the secret key, and we let $t$ be the time required to compute $f(K,P)$ for keys $K$ of length $\ell$ (we assume here that the length of $P$ and the method of computing $f$ has been fixed). To measure the serious of the attack, we use a factor $\alpha$ and an attack time $s$. The factor $\alpha$ is the ratio of the computational power available to the attacker to the computational power of the computer used for computing $f(K,P)$. The value $\alpha$ includes the following factors:

• the amount of parallelism available to the attacker (usually equal to the number of computers at his disposal)
• the faster speed of the attacker's computers. This may be non-trivial when $f$ is computed by a slow machine and the attacker has very powerful computers. One should also consider how long the cryptosystem should remain secure and the increased speed of future computers.
• allowance for our lack of confidence that we know the best way to compute the slow function $f$.

The time value $s$ is the amount of real time the attacker is willing to spend, or has available, to attack the short key system.

Since there are $2^\ell$ potential secret keys, the system is deemed to be safe from attackers provided

$$2^\ell\cdot t ~> >~ \alpha\cdot s.$$

Or to restate this, the time it would take the adversary to exhaustively try all possible $\ell$ bit secret keys is

$$\frac {2^\ell \cdot t} \alpha.$$

To give some feeling for the security levels, the Tables 1-3 list values of this adversarial time for three values of $\ell$ and various values of $t$. To make some sense of the values of $\alpha$, one might consider that $\alpha=1000$ corresponds to an attacker harnessing the power of a large number of computers in a single organization to try potential secret keys in parallel; the value $\alpha=1,000,000$ might represent the effort of a government making a determined and expensive attack with a large number of small dedicated computers; and the value $\alpha = 1,000,000,000$ could represent a multiyear large-scale government attack or could represent the power of most of the personal computers in the world working in parallel.

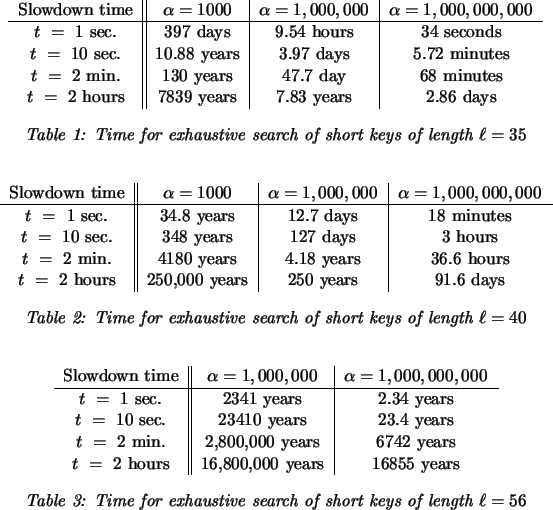
For true security, one probably should use a value of $\alpha\ge 1,000,000$; however the smaller value $\alpha=1000$ might be acceptable for low security applications. For security against a ``worldwide'' attack where $\alpha=10^9$, one probably should use short keys of length closer to 56.

One tradeoff in picking the slowdown time $t$ is that the time cannot be so long as to impede the implementation of the cryptographic protocol. If Alice and Bob's secure connection is to be long-lived, then a quite long slowdown may be reasonable, providing additional security. An initial one time slowdown of hours, or even days or longer, might be acceptable; later, new expanded keys may be generated by running $f$ again with its execution overlapped with the communication session in progress so that no further delays are experienced.

Finally, it is stressed that the public auxiliary keys must be chosen to minimize the likelihood that two sessions will use the same one. Combining some random bits (say 40) with the encoded standard date and time is a natural approach.

Candidates for slow one-way functions

A slow one-way function $f$ must enjoy the following hardness properties, which generalize the usual notion of one-way-ness:

1.

The must be some reliable estimate $t_f$ for a lower bound on the time to compute a value of $f(x)$ with a given amount of computational hardware.

2.

Given a value $z=f(x)$ it must be hard to determine the value $x$ in the sense that one cannot do much better than exhaustive search which considers all possible values of $x$ and computes $f(x)$ for each of them. In particular, there is no way to test whether $z=f(x)$ in time significantly less than $t_f$. In addition, this search is not parallelizable in the sense that for any set $X=\{x_i\}_i$ of cardinality $N$, it takes time about $N\cdot t_f$ to determine which whether $z\in f(X)$ (with the same given amount of hardware as in 1.).

3.

Furthermore the one-way-ness must be robust under the presence of auxiliary keys. Namely, if an adversary is given values $P_1,\ldots,P_k$ and given the values $z_i=f(\langle K,P_i\rangle)$ it should still take the same amount of time to determine $K$.

Of course, the search problem for $f$ is inherently parallelizable; so an adversary who is able to use a large amount of hardware can speed up the exhaustive search for the value of $x$. This is of course part of the reason for our use of the parameter $\alpha$ in the previous section.

As we remarked before, any slow function can be converted into a slow one-way function merely by composing the slow function with a one-way function. Thus, practically speaking, it is sufficient to find good candidates for slow functions, since from this one can readily create a slow one-way function.

A natural choice for the slow function $f$ is to base in on iteration of the pseudorandom number generator $g$. Letting $g$ be a strong pseudorandom number generator with a sufficiently large internal state that maps $m$ bit numbers to $m$ bit numbers, one can form an initial seed  $\sigma=\sigma(K,P)$ and then apply $g$ repeatedly to the seed until the desired slowdown is achieved. One or more subsequent values of $g$ is then read out and hashed to generate the expanded key $E$. It is easy to generate an extended key of any length using this scheme so that it might be used to generate a 56-bit DES key, or several for repeated DES, etc.

An important consideration when choosing a slow function $f$ is whether it is possible to build special, custom hardware that accelerates the computation of values of the function $f$. In particular, if it is difficult to get a large speedup with custom hardware, then one does not need to use such a large value for $\alpha$. The pseudorandom generator approach above is attractive because processors in widespread use can evaluate functions like this very efficiently with the computation taking place entirely within cache memory. Moreover, it is inherently sequential, guarding against a parallel attack. For these reasons, it is unlikely that supercomputers or even special purpose hardware can provide a major improvement in the time needed to compute a single value of the function $f$ based on such a pseudorandom number generator.

One possible problem with above pseudorandom number generator method is that one must ensure that it is not possible to quickly compute multiple iterations of $g$; this is not a general design requirement for pseudorandom number generators, although doubtlessly most pseudorandom number generators have this property. To be more careful with this, one might combine the pseudorandom generator $g$ with a one parameter family of one-way permutations $h_w$. (Candidates for $h$ include many of the standard symmetric key cryptographic functions, including DES, etc., where the parameter $w$ serves as the secret key for the cryptographic function. One should use DES for this only if a hardware implementation is available.) Then make the parameter $w$ a function of $K$ and $P$ and set $\sigma_1 = \sigma = \sigma(K,P)$ as before, and set $\sigma_{i+1} = h_w(\sigma_i)\oplus g^i(\sigma)$ where $g^i$ denotes the $i$-fold iteration of $g$. Choosing a value $i_0$ large enough so that the computation of $\sigma_{i_0}$ requires run time $t$, one can use $\sigma_{i_0}$ (and possibly a few subsequent $\sigma_i$'s if more bits are needed) to form the expanded key $E$.

Quisquater et al. [9] proposed iterated DES as a slowdown function for key generation. Several other authors have suggested functions with purposeful slowdowns, for other applications. For the application of uncheatable benchmarks, Cai et al.[4] propose iterated powering modulo a product of two large primes; as a second proposal, they suggest a one-way benchmark where one uses a one-way function $f$ and a hash function $h$ and the slow problem is the problem of finding a value $x$ so that $f(h(x))=z$ for a given value $z$. By controlling the size of the set from which $x$ is drawn they control the runtime of a procedure which finds $x$ from $z$. Dwork and Naor [5] propose slow functions as means of reducing junk email. Their suggestions for slow functions include extracting square roots modulo a prime $p$, with $p$ carefully chosen so that the expected time to find a square root can be controlled. Rivest, Shamir and Wagner [11] suggest time-lock cryptography which depend on tailoring the computation runtime of a problem: they also suggest iterated powering modulo a product of two large primes as a slow function. It should be noted that iterated power modulo the product of two large primes (as suggested by [4,11]) is not so good for our application, unless one is able to completely discard all knowledge of the two large primes; this is because knowledge of the primes would open a trapdoor that would circumvent the the slowness of the slow one-way function.

Conclusion

We have shown that slow key expansion may be used to construct secure public key or symmetric cryptosystems in which very little secret knowledge is required. A 40-bit secret, for example, may be remembered as eight alphanumeric symbols or only three entries drawn from a 10,322 word dictionary of common English words. Security is enhanced because secret keys this small can be remembered by the owners and may never be stored for any long period in the cryptosystem itself. When used with auxiliary nonsecret keys, short secret keys can be used as master keys in a key generation protocol and allow multiple independently secure communication sessions.

Acknowledgement We thank Mihir Bellare, Russell Impagliazzo and Francis Zane for helpful comments on a draft of this paper.

Bibliography

1

M. BELLARE AND S. GOLDWASSER, Encapsulated key escrow.
Typseset manuscript, at http://www-cse.ucsd.edu/users/mihir, 1996.

2

height 2pt depth -1.6pt width 23pt, Verifiable partial key escrow.
Typseset manuscript, at http://www-cse.ucsd.edu/users/mihir, to appear in Proc. 4th ACM Conf. on Computer and Communications Security, 1997.

3

M. BLAZE, W. DIFFIE, R. RIVEST, B. SCHNEIER, T. SHIMOMURA, E. THOMPSON, AND M. WIENER, Minimal key lengths for symmetric ciphers to provide adequate commercial security: A report by an ad hoc group of cryptographys and computer scientists.
Typeset manuscript, 1995.

4

J.-Y. CAI, R. J. LIPTON, R. SEDGEWICK, AND A. C.-C. YAO, Towards uncheatable benchmarks, in Proceedings of the 8th Annual Conference on Structure in Complexity Theory (SCTC '93), IEEE Computer Society Press, 1993, pp. 2-11.

5

C. DWORK AND M. NAOR, Pricing via processing or combatting junk mail, in Advances in Cryptology--CRYPTO '92, E. F. Brickell, ed., Lecture Notes in Computer Science #740, Springer-Verlag, 1993.

6

W. F. EHRSAM, S. M. MATYAS, C. H. MEYER, AND W. L. TUCHMAN, A cryptographic key management scheme for implementing the Data Encryption Standard, IBM Systems Journal, 17 (1978), pp. 106-125.

7

S. M. MATYAS AND C. H. MEYER, Generation, distribution and installation of cryptographic keys, IBM Systems Journal, 17 (1978), pp. 126-137.

8

A. J. MENEZES, P. C. VAN OORSHOT, AND S. A. VANSTONE, Handbook of Applied Cryptography, CRC Press, Boca Raton, 1997.

9

J.-J. QUISQATAR, Y. DESMEDT, AND M. DAVIO, The importance of ``good'' key scheduling schemes (how to make a secure DES scheme with $\le 48$ bit keys, in Advances in Cryptology-CRYPTO'85, H. C. Williams, ed., Lecture Notes in Computer Science #218, Springer Verlag, 1985, pp. 537-542.

10

R. L. RIVEST, All-or-nothing encryption and the package transform, in 4th International Workshop on Fast Software Encryption, FSE'97, E. Biham, ed., Lecture Notes in Computer Science #1267, Springer Verlag, 1997, pp. 210-218.

11

R. L. RIVEST, A. SHAMIR, AND D. A. WAGNER, Time-lock puzzles and timed-release crypto.
Typeset manuscript, at http://theory.lcs.mit.edu/$\sim$rivest, 1996.

12

B. SCHNEIER, Applied Cryptography, J.Wiley and Sons, New York, 1996.

About this document ...

Secure Short-Key Cryptosystems:
Forty Bits is Enough

This document was generated using the LaTeX2HTML translator Version 2K.1beta (1.47)

Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.

The command line arguments were:
latex2html -split 0 -image_type gif -nonext_page_in_navigation -noprevious_page_in_navigation -up_url ../main.html -up_title 'Publication homepage' -accent_images textrm -numbered_footnotes sk.tex

The translation was initiated by Peter N. Yianilos on 2002-06-25

Footnotes

... Buss¹

Partially supported by NSF grants DMS-9503247 and DMS-9803515. Email: sbuss@ucsd.edu.

... Yianilos²

Email: pny@cs.princeton.edu.

... conjunction).³

We presume the reader is familiar with the basics of cryptographic protocols; two good sources for this are [12,8].

... bits.⁴

The examples below will show that a 36 bit key is often quite adequate.

... here.⁵

Indeed, the second example is the name of an earthquake safety device! This is obviously a very bad choice; but also any non-random choice will reduce significantly reduce the effective length of the secret key.

....⁶

The security of the short secret key even under loss of a some expanded keys is the only reason for needing $f$ to be one-way.

... channel.⁷

Often, Alice and Bob want the conversation to be secure in both directions, in which case, Bob has his own short secret key $K^\prime$ and generates his own auxiliary key $P^\prime$: from these he uses the slow one-way $f$ to compute his pair of private/public keys for $C$. For simplicity, we shall discuss only Alice's situation.