Samuel R. Buss 2. - Peter N. Yianilos 3.
We report a new and very fast algorithm for an abstract
special case of this problem. Our first requirement is that
the nodes of the graph are given as a `quasi-convex tour'.
This means that they are provided circularly ordered as
![]() where
where
![]() , and that for any
, and that for any
![]() , not necessarily adjacent but in tour
order, with
, not necessarily adjacent but in tour
order, with ![]() of one color and
of one color and ![]() of the
opposite color, the following inequality holds:
of the
opposite color, the following inequality holds:
If ![]() , our algorithm then finds a minimum-cost
matching in
, our algorithm then finds a minimum-cost
matching in ![]() time. Given an additional
condition of `weak analyticity', the time complexity is
reduced to
time. Given an additional
condition of `weak analyticity', the time complexity is
reduced to ![]() . In both cases only linear space is
required. In the special case where the circular ordering is
a line-like ordering, these results apply even if
. In both cases only linear space is
required. In the special case where the circular ordering is
a line-like ordering, these results apply even if
![]() .
.
Our algorithm is conceptually elegant, straightforward to implement, and free of large hidden constants. As such we expect that it may be of practical value in several problem areas.
Many natural graphs satisfy the quasi-convexity condition. These include graphs which lie on a line or circle with the canonical tour ordering, and costs given by any concave-down function of arclength -- or graphs whose nodes lie on an arbitrary convex planar figure with costs provided by Euclidean distance.
The weak-analyticity condition applies to points lying on a
circle with costs given by Euclidean distance, and we thus
obtain the first linear-time algorithm for the minimum-cost
matching problem in this setting (and also where costs are
given by the ![]() or
or ![]() metrics).
metrics).
Given two symbol strings over the same alphabet, we may imagine one to be red and the other blue, and use our algorithms to compute string distances. In this formulation, the strings are embedded in the real line and multiple independent assignment problems are solved; one for each distinct alphabet symbol.
While these examples are somewhat geometrical, it is important to remember that our conditions are purely abstract; hence, our algorithms may find application to problems in which no direct connection to geometry is evident.
![]()
![]()
The minimum-cost matching problem is substantially easier in the case
where the nodes are in line-like order or are circularly ordered. The
simplest versions of line-like/circular orderings are where the points
lie on a line or lie on a curve homeomorphic to a circle, and the cost
![]() of an edge between
of an edge between ![]() and
and ![]() is equal to the shortest
arclength distance between the nodes. The matching problem for this
arclength cost function has been studied by
Karp-Li [14],
Aggarwal et al. [1],
Werman et al. [23] and others, and is the `Skis and
Skiers' problem of Lawler [18]. Karp-Li have
given linear time algorithms for this matching problem;
Aggarwal et al. have generalized the linear time algorithm to the
transportation problem.
is equal to the shortest
arclength distance between the nodes. The matching problem for this
arclength cost function has been studied by
Karp-Li [14],
Aggarwal et al. [1],
Werman et al. [23] and others, and is the `Skis and
Skiers' problem of Lawler [18]. Karp-Li have
given linear time algorithms for this matching problem;
Aggarwal et al. have generalized the linear time algorithm to the
transportation problem.
A more general version of the matching problem for graphs in line-like
order has been studied by
Gilmore-Gomory [10]
(see [18]). In this version, the cost of an
edge from a red node ![]() forward to a blue node
forward to a blue node ![]() is defined to
equal
is defined to
equal ![]() and from a blue node
and from a blue node ![]() forward to a red node
forward to a red node ![]() to equal
to equal ![]() , for some functions
, for some functions ![]() and
and ![]() . This matching
problem has a linear time algorithm provided
. This matching
problem has a linear time algorithm provided ![]() .
.
Another version of the matching problem for line-like graphs is considered by Aggarwal et al.[1]: they use graphs which satisfy a ``Monge'' property which states that the inequality (1.1) below holds except with the inequality sign's direction reversed. They give a linear time algorithm for the matching problem for (unbalanced) Monge graphs.
In the prior work most closely related to this paper, Marcotte and
Suri [20] consider the matching problem
for a circularly ordered, balanced tour in which the nodes are the
vertices of a convex polygon and the cost function is equal to
Euclidean distance. This matching problem is substantially more
complicated than the comparatively simple `Skis and Skiers' type
problems; nonetheless, Marcotte and Suri give an ![]() time
algorithm which solves this minimum-cost matching problem. For the
case where the nodes are the vertices of a simple polygon and the cost
function is equal to the shortest Euclidean distance inside the
polygon, they give an
time
algorithm which solves this minimum-cost matching problem. For the
case where the nodes are the vertices of a simple polygon and the cost
function is equal to the shortest Euclidean distance inside the
polygon, they give an ![]() time algorithm.
time algorithm.
The main results of this paper apply to all the above matching
problems on circularly ordered or line-like tours, with the sole
exception of unbalanced, Monge graphs. For the `Skis and Skiers'
and the Gilmore-Gomory problems, Theorem 1.9 gives new linear
time algorithms which find minimum-cost matchings which are different
than the traditional minimum-cost matchings (and our algorithms are
more complicated than is necessary for these simple problems). Our
algorithms subsume those of Marcotte and Suri and give some
substantial improvements: First, with the weak analyticity condition,
we have linear time algorithms for many important cases, whereas
Marcotte and Suri's algorithm takes ![]() time. Second, our
assumption of quasi-convexity is considerably more general than their
planar geometrical setting and allows diverse applications. Third,
our algorithms are conceptually simpler than the divide-and-conquer
methods used by Marcotte and Suri, and we expect that our algorithms
are easier to implement.
time. Second, our
assumption of quasi-convexity is considerably more general than their
planar geometrical setting and allows diverse applications. Third,
our algorithms are conceptually simpler than the divide-and-conquer
methods used by Marcotte and Suri, and we expect that our algorithms
are easier to implement.
All of our algorithms have been implemented as reported in [5]; a brief overview of this implementation is given in section 3.4.
We list some sample applications of our algorithms in Examples 1-8 below. One example of a matching problem solution is shown in Figure 1.1. For this figure, a 74 node bipartite graph was chosen with nodes on the unit circle. For this matching problem, the cost of an edge is equal to the Euclidean distance between its endpoints. The edges shown form a minimum-cost matching.

|
Our quasi-convex property is equivalent to the ``inverse quadrangle inequality'' used, for instance, by [8], but is weaker than the similar ``inverse Monge property'' of [4]. In fact, we show below that any Monge matching problem may be trivially transformed into a quasi-convex matching problem, but not vice-versa.
Dynamic programming problems based on cost functions which satisfy the (inverse) quadrangle inequality and some closely related matrix-search problems have been studied by many authors, including [,,,,,,,,,,,,]. However, we have discovered no direct connection between our quasi-convex matching problem and the problems solved by these authors.
The notion of a Monge array [13] is
related to that of quasi-convexity, but the Monge condition is a
stronger (i.e., quasi-convexity is strictly more general). Because of
the similarity between the definitions of both properties, we take the
time to illustrate this point in detail. To understand the Monge
property in our bipartite setting, imagine the cost function to be an
array, and impose the restriction that its first argument select a red
point, and the second a blue point. The array is Monge provided that
for all ![]() satisfying
satisfying
![]() and
and
![]() , we have:
, we have:
However not every quasi-convex tour can be rearranged to form a Monge
array. We will now exhibit such a quasi-convex tour. Its nodes lie
along the real line, and costs are given by the square root of
inter-node distance; tour order is from left to right. Given a
subtour of the form
![]() , then it is easily shown that in
any Monge reordering,
, then it is easily shown that in
any Monge reordering, ![]() iff
iff ![]() .
Similarly, given a tour of the form
.
Similarly, given a tour of the form
![]() ,
, ![]() iff
iff ![]() . Our counterexample then consists of any
tour having a subtour of the form:
. Our counterexample then consists of any
tour having a subtour of the form: ![]() . To understand
why, we attach subscripts resulting in
. To understand
why, we attach subscripts resulting in
![]() and proceed to apply the two rules above to get the implications:
and proceed to apply the two rules above to get the implications:
We now give the definitions necessary to state the main results of
this paper. We think of the nodes of the graph ![]() as being either a
line-like or circular tour of the graph; in the case of a circular
tour, we think of the node
as being either a
line-like or circular tour of the graph; in the case of a circular
tour, we think of the node ![]() as following again after
as following again after ![]() .
.
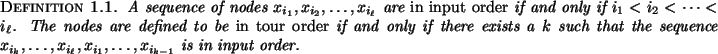
Reordering terms in (1.1) gives
To give a geometric intuition to quasi-convexity, note that
when
![]() are the vertices of a quadrilateral, the
inequality states that the sum of the lengths of diagonals is greater
than or equal to the sum of the lengths of two of the sides.
are the vertices of a quadrilateral, the
inequality states that the sum of the lengths of diagonals is greater
than or equal to the sum of the lengths of two of the sides.
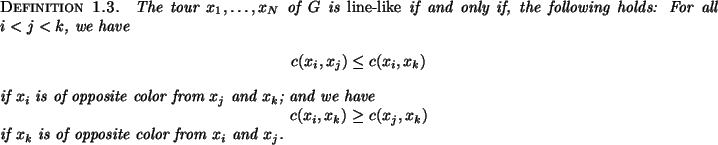
The property of quasi-convexity is defined independently of the starting point of the tour; i.e., the nodes of the tour can be `rotated' without affecting quasi-convexity. Obviously, the definition of line-like tours is sensitive to the choice of starting point of the tour.
Our main theorems give either ![]() or
or ![]() time algorithms
for all of the following examples, with the exception of example 7:
time algorithms
for all of the following examples, with the exception of example 7:
Remark: The running times of the algorithms are given
in terms of the number ![]() of nodes, even though the input size may in
some cases need to be
of nodes, even though the input size may in
some cases need to be ![]() to fully specify the values of the
cost function. However, in all the examples above, the input size is
to fully specify the values of the
cost function. However, in all the examples above, the input size is
![]() since the cost function is specified by the nodes' positions on
a line, on a curve, or in the plane. In any event, our runtime
analysis assumes that any value
since the cost function is specified by the nodes' positions on
a line, on a curve, or in the plane. In any event, our runtime
analysis assumes that any value ![]() of the cost function can
be computed in constant time. If this is not the case, then the
runtimes are to be multiplied by the time needed to compute a value of
the cost function; this is the situation in example 7 above.
of the cost function can
be computed in constant time. If this is not the case, then the
runtimes are to be multiplied by the time needed to compute a value of
the cost function; this is the situation in example 7 above.
We next define an ``weak analyticity'' condition which will allow yet faster algorithms.
It is not hard to see that the property of quasi-convexity implies
that, if the ![]() -crossover point
-crossover point ![]() exists, then
exists, then
![]() whenever
whenever
![]() are in tour order and
are in tour order and
![]() whenever
whenever
![]() are in tour order. Thus binary search provides
an
are in tour order. Thus binary search provides
an ![]() -time procedure which, given
-time procedure which, given ![]() ,
, ![]() and
and ![]() ,
will determine if
,
will determine if ![]() exists and, if so, which node
exists and, if so, which node ![]() is. This
is the approach taken in the algorithms of Theorem 1.4,
and is the source of the
is. This
is the approach taken in the algorithms of Theorem 1.4,
and is the source of the ![]() factor in the runtime. However, in
some cases,
factor in the runtime. However, in
some cases, ![]() can be found in constant time and we define:
can be found in constant time and we define:
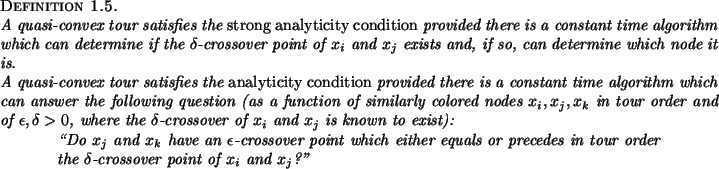
Even the analyticity condition is too strong to be satisfied in many situations, so we also define a `weak analyticity condition' as follows.

![]()
Clearly the strong analyticity condition implies the analyticity
condition, which in turn implies the weak analyticity condition. In
most applications, we do not have the analyticity or strong
analyticity conditions, but the weak analyticity condition does hold
in many natural situations. In particular, examples 1, 2, 3 and 4 do
satisfy the weak analyticity condition, provided that the concave-down
function is sufficiently natural. Consider, for instance, example 1
with the concave-down function ![]() ,
, ![]() , or
, or ![]() , etc. For example 1, the input nodes
, etc. For example 1, the input nodes
![]() are given
with a sequence of real numbers
are given
with a sequence of real numbers
![]() which
are the positions of the nodes on the real line. Given nodes
which
are the positions of the nodes on the real line. Given nodes ![]() ,
,
![]() and
and ![]() , the first possible position for the
, the first possible position for the
![]() -crossover of
-crossover of ![]() and
and ![]() can be found by solving the
equation
can be found by solving the
equation
![]() for
for ![]() ; since we assume that
arithmetic operations take constant time, the solution
; since we assume that
arithmetic operations take constant time, the solution ![]() can be
found in constant time. Note that
can be
found in constant time. Note that ![]() is only the theoretical
crossover point; the actual crossover is the first node
is only the theoretical
crossover point; the actual crossover is the first node ![]() such
that
such
that ![]() . Unfortunately, even after
. Unfortunately, even after ![]() is known, it will not
be possible to determine
is known, it will not
be possible to determine ![]() in constant time, unless some
additional information is given about the distribution of the nodes on
the real line. Thus, the analyticity condition and strong analyticity
conditions do not hold in general for example 1. The reason the
analyticity condition does not hold is that, if the theoretical
in constant time, unless some
additional information is given about the distribution of the nodes on
the real line. Thus, the analyticity condition and strong analyticity
conditions do not hold in general for example 1. The reason the
analyticity condition does not hold is that, if the theoretical
![]() -crossover point occurs after the theoretical
-crossover point occurs after the theoretical
![]() -crossover point, then the analyticity algorithm must output
`No' if there is a node after the theoretical
-crossover point, then the analyticity algorithm must output
`No' if there is a node after the theoretical ![]() -crossover point
and before or at the theoretical
-crossover point
and before or at the theoretical ![]() -crossover point, and must
output `Yes' otherwise (because in the latter case the two actual
crossover points coincide). Unfortunately, there is no general way to
decide this in constant time, so the analyticity condition is false.
However, the weak analyticity condition does hold, since the function
-crossover point, and must
output `Yes' otherwise (because in the latter case the two actual
crossover points coincide). Unfortunately, there is no general way to
decide this in constant time, so the analyticity condition is false.
However, the weak analyticity condition does hold, since the function
![]() may operate by computing the theoretical
may operate by computing the theoretical ![]() -crossover
of
-crossover
of ![]() and
and ![]() and the theoretical
and the theoretical ![]() -crossover of
-crossover of
![]() and
and ![]() and outputting ``Yes'' if the former is less than the
latter.
and outputting ``Yes'' if the former is less than the
latter.
For similar reasons, example 3 satisfies the weak analyticity
condition: in this case, since the nodes lie on a circle and the cost
function is Euclidean distance, the theoretical crossover position is
computed (in constant time) as the intersection of a hyperbola and the
circle. Likewise, the weak analyticity condition also holds for
example 2 if the concave-down function is sufficiently nice, and it
holds for example 6, where nodes lie on a circle under the ![]() and
and
![]() metrics. Example 4, where the nodes form the vertices of a
convex polygon, does not seem to satisfy the weak analyticity
condition in general; however, some important special cases do. For
example, if the vertices of the convex polygon are known to lie on a
polygon with a bounded number of sides, on an oval, or on a branch of
a hyperbola, then the weak analyticity condition does hold.
metrics. Example 4, where the nodes form the vertices of a
convex polygon, does not seem to satisfy the weak analyticity
condition in general; however, some important special cases do. For
example, if the vertices of the convex polygon are known to lie on a
polygon with a bounded number of sides, on an oval, or on a branch of
a hyperbola, then the weak analyticity condition does hold.
The analyticity condition has been implicitly used by
Hirschberg-Larmore [12] who defined a
Bridge function which is similar to our ![]() function: they
give a special case in which Bridge is constant-time computable
and thus the analyticity condition holds. Later,
Galil-Giancarlo [8] defined a ``closest
zero property'' which is equivalent to our strong analyticity
condition.4 As we illustrated above, the analyticity and strong
analyticity conditions rarely hold. Thus it is interesting to note
that the algorithms of Hirschberg-Larmore and of Galil-Giancarlo will
still work, with only minor modifications, if only the weak
analyticity condition holds.
function: they
give a special case in which Bridge is constant-time computable
and thus the analyticity condition holds. Later,
Galil-Giancarlo [8] defined a ``closest
zero property'' which is equivalent to our strong analyticity
condition.4 As we illustrated above, the analyticity and strong
analyticity conditions rarely hold. Thus it is interesting to note
that the algorithms of Hirschberg-Larmore and of Galil-Giancarlo will
still work, with only minor modifications, if only the weak
analyticity condition holds.
Our second main theorem implies that these examples which satisfy the weak analyticity condition have linear time algorithms for minimum-cost matching:
Remark: In order to achieve the linear time algorithms, it is necessary that nodes of the graph be input in their tour order. This assumption is necessary, since without it, it is possible to give a linear time reduction of sorting to the matching problem for line-like tours.
Our main theorems also apply to minimum-cost matchings for some
non-bipartite quasi-convex tours. If a non-bipartite graph ![]() has
has
![]() nodes and has cost function
nodes and has cost function ![]() , then a matching for
, then a matching for ![]() is a set
of
is a set
of
![]() edges with all endpoints distinct. Parts (i) of Main
Theorems 1.4 and 1.9 hold also for non-bipartite
graphs which are line-like quasi-convex tours. And parts (ii) of Main
Theorems 1.4 and 1.9 hold also for non-bipartite
graphs which are quasi-convex tours with an even number of nodes. The
non-bipartite cases are discussed in section 4; the algorithms are
simple modifications of the algorithms for the bipartite tours.
edges with all endpoints distinct. Parts (i) of Main
Theorems 1.4 and 1.9 hold also for non-bipartite
graphs which are line-like quasi-convex tours. And parts (ii) of Main
Theorems 1.4 and 1.9 hold also for non-bipartite
graphs which are quasi-convex tours with an even number of nodes. The
non-bipartite cases are discussed in section 4; the algorithms are
simple modifications of the algorithms for the bipartite tours.
It is apparent that our algorithms can be parallelized but we have not
investigated the precise runtime and processor count that is needed
for a parallel implementation. He [11] has
given a PRAM implementation of Marcotte and Suri's algorithm which
uses ![]() processors and
processors and ![]() time and it is clear that our
algorithm can be computed with the same number of processors with the
same time bounds using He's methods.
time and it is clear that our
algorithm can be computed with the same number of processors with the
same time bounds using He's methods.
Our algorithms apply only to unbalanced tours only if they are line-like. This is because in the line-like case the leveling process, described in the next section, induced by choosing the first node as starting point, is guaranteed to decompose the problem into alternating color sub-problems, which may be independently solved and reassembled to produce an overall solution. Now some of these sub-problems may be unbalanced, but again using using the line-like property, we are able to force balance by adding a dummy node when necessary. These then are two different uses of the line-like property.
In balanced, unimodal tours5such as the circle, the leveling concept of section 2 holds in a
weaker form. However, we have been unable to extend our results to
the unbalanced unimodal case. As an example of the difficulty of
this, consider the highly eccentric ellipse of Figure 1.3;
the bipartite tour containing its four nodes is unbalanced and is
neither line-like nor unimodal. Notice that no starting point induces
a leveling which places ![]() and
and ![]() at the same level - despite
the fact that the minimum cost matching consists of an edge between
them. The path to extending our methods to such cases is therefore
less clear.
at the same level - despite
the fact that the minimum cost matching consists of an edge between
them. The path to extending our methods to such cases is therefore
less clear.
![\begin{definition}
Let $x_i$\ and $x_j$\ be nodes. We write $[x_i,x_j]$\ to deno...
...ightarrow x_\ell$\ with $x_i, x_j, x_k, x_\ell$\ in
tour order.
\end{definition}](img110.gif)
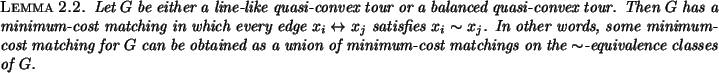
To prove Lemma 2.2 we use:
![]()
proof: (Sketch) If a minimum-cost matching does have a pair of jumpers which cross, the quasi-convexity property allows them to be `uncrossed' without increasing the total cost. Repeatedly uncrossing jumpers will eventually yield a minimum-cost matching with no crossing jumpers. (See Lemma 1 of [1] for a detailed proof of this.)
Lemma 2.2 is proved by noting that a minimum-cost matching
with no crossing jumpers must respect the ![]() -equivalence classes.
This is because, if a jumper
-equivalence classes.
This is because, if a jumper
![]() is in a crossing-free
matching with
is in a crossing-free
matching with ![]() , then the nodes in the interval
, then the nodes in the interval ![]() must
be matched with each other and thus
must
be matched with each other and thus ![]() must have equal
numbers of red and blue nodes. In the unbalanced, line-like case,
this also depends on the fact that, w.l.o.g., there is no jumper which
crosses an unmatched node (this is an immediate consequence of the
line-like condition).
must have equal
numbers of red and blue nodes. In the unbalanced, line-like case,
this also depends on the fact that, w.l.o.g., there is no jumper which
crosses an unmatched node (this is an immediate consequence of the
line-like condition).![]()
By Lemma 2.2, in order to find a minimum-cost matching, it
suffices to extract the ![]() -equivalence classes, and find
minimum-cost matchings for each equivalence class independently. It
is an easy matter to extract the
-equivalence classes, and find
minimum-cost matchings for each equivalence class independently. It
is an easy matter to extract the ![]() -equivalent classes in linear
time by using straightforward counting. Each equivalence class
consists of an alternating color subtour: in the balanced case, there
are an even number of nodes in each equivalence class, and in the
line-like condition case, there may be an even or odd number of nodes.
Thus, to give (near) linear time algorithms for finding matchings, it
will suffice to restrict our attention to tours in which the nodes are
of alternating colors.
-equivalent classes in linear
time by using straightforward counting. Each equivalence class
consists of an alternating color subtour: in the balanced case, there
are an even number of nodes in each equivalence class, and in the
line-like condition case, there may be an even or odd number of nodes.
Thus, to give (near) linear time algorithms for finding matchings, it
will suffice to restrict our attention to tours in which the nodes are
of alternating colors.
In view of Lemma 2.3, we may restrict our attention to matchings which contain no crossing jumpers. Such a matching will be called crossing-free.
Finally, we can assume w.l.o.g. that the tour is balanced. To see why
we can assume this, suppose that
![]() is an unbalanced,
line-like tour of alternating colors. This means that
is an unbalanced,
line-like tour of alternating colors. This means that ![]() and
and ![]() are the same color, say red. We can add a new node
are the same color, say red. We can add a new node ![]() to the
end of the tour, label it blue, and let
to the
end of the tour, label it blue, and let
![]() for all
red
for all
red ![]() . These
. These ![]() nodes no longer form a line-like tour;
however, they do form a balanced quasi-convex tour. Solving the
matching problem for the
nodes no longer form a line-like tour;
however, they do form a balanced quasi-convex tour. Solving the
matching problem for the ![]() nodes immediately gives a solution to
the matching problem on the original
nodes immediately gives a solution to
the matching problem on the original ![]() nodes.
nodes.
The notation ![]() has already been defined. In addition, the
notation
has already been defined. In addition, the
notation ![]() denotes the interval of integers
denotes the interval of integers
![]() if
if
![]() , or the (circular) interval
, or the (circular) interval
![]() if
if
![]() . We also use the notations
. We also use the notations ![]() ,
, ![]() and
and ![]() for the intervals with one or both of the endpoints omitted.
for the intervals with one or both of the endpoints omitted.
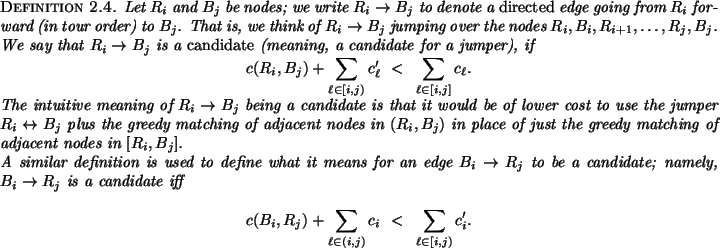
Candidates always have endpoints of opposite colors and are directed.
It is possible to have both
![]() and
and
![]() be
(distinct) candidates, or to have one or neither of them candidates.
be
(distinct) candidates, or to have one or neither of them candidates.
It is an easy observation that if there are no candidates, then the
greedy assignment(s) are minimum-cost matchings. To prove this,
suppose ![]() is a minimum-cost matching which contains a jumper:
by Lemma 2.3,
is a minimum-cost matching which contains a jumper:
by Lemma 2.3, ![]() may be picked to contain no
crossing jumpers. Since there are no crossing jumpers,
may be picked to contain no
crossing jumpers. Since there are no crossing jumpers, ![]() must
contain a jumper
must
contain a jumper
![]() such that
such that ![]() is greedy on
is greedy on
![]() (namely, pick the jumper so as to minimize the tour-order
distance from
(namely, pick the jumper so as to minimize the tour-order
distance from ![]() to
to ![]() ). Let
). Let ![]() be the matching
which is the same as
be the matching
which is the same as ![]() , except greedy on
, except greedy on ![]() . Clearly
. Clearly
![]() has one fewer jumper than
has one fewer jumper than ![]() , and since
, and since
![]() is not a candidate,
is not a candidate, ![]() has cost no greater than
has cost no greater than
![]() . Iterating this construction shows that at least one of the
jumper-less greedy matchings must be minimum-cost. To show they are
both minimum-cost, let
. Iterating this construction shows that at least one of the
jumper-less greedy matchings must be minimum-cost. To show they are
both minimum-cost, let ![]() and
and ![]() be the greedy
matchings which contain the edges
be the greedy
matchings which contain the edges
![]() and
and
![]() ,
respectively. Then
,
respectively. Then ![]() can not have cost lower than
(respectively, higher than) the cost of
can not have cost lower than
(respectively, higher than) the cost of ![]() since otherwise,
since otherwise,
![]() (
(
![]() , respectively) would be a candidate.
, respectively) would be a candidate.
![]()
Note that Lemma 2.6 says only that the edges
connecting adjacent nodes in the interior of the minimal
candidate are in every minimum-cost matching; it does not say that the
minimal candidate itself is a jumper in any minimum-cost matching.
The proof of Lemma 2.6 is fairly involved and we
postpone it until section 2.3. Lemma 2.6 also
holds for line-like tours with alternating colors for candidates
![]() with
with ![]() in input order.
in input order.
Lemma 2.6 suggests an algorithm for finding a minimum-cost matching. Namely, if there is a minimal candidate, greedily assign edges in its interior according to Lemma 2.6. This induces a matching problem on the remaining unassigned nodes, and it is clear that any minimum-cost matching on this smaller problem will lead to a minimum-cost matching for the original problem. Iterating this, one can continue removing nodes in the interiors of minimal candidates and reducing the problem size. Eventually a matching problem with no candidates will be reached; in this case, it suffices to greedily match the remaining nodes.
Unfortunately, this algorithm suggested by
Lemma 2.6 is not linear time (yet); thus we need to
refine Lemma 2.6 somewhat:
![\begin{definition}
We define:
\begin{eqnarray*}
\mbox{\sf Bnft}[R_a,B_b] & = &
...
...r $x$\ and $y$\ the same color, $\mbox{\sf Bnft}[x,y]=-\infty$.
\end{definition}](img164.gif)
It is immediate that
![]() iff
iff
![]() is a candidate; in
fact,
is a candidate; in
fact,
![]() measures the benefit (i.e., the reduction in cost),
of using
measures the benefit (i.e., the reduction in cost),
of using
![]() as a minimal jumper instead of the greedy matching
on
as a minimal jumper instead of the greedy matching
on ![]() .
.
The next lemma forms the basis for the correctness of the algorithm
given in section 3 for the serial transitive closure problem. The
general idea is that the algorithm will scan the nodes in tour order
until at least one candidate is found and then, according to
Lemma 2.8, the algorithm will choose an interval
![]() to greedily match. Once the interval
to greedily match. Once the interval ![]() has
been greedily matched, the algorithm need only solve the induced
matching problem on the remaining nodes.
has
been greedily matched, the algorithm need only solve the induced
matching problem on the remaining nodes.

proof: The proof is, in essence, an iteration of
Lemma 2.6. We argue by induction on ![]() . Let
. Let ![]() ,
,
![]() ,
, ![]() and
and ![]() satisfy the hypothesis of the lemma. Let
satisfy the hypothesis of the lemma. Let
![]() , so
, so
![]() is a minimal
candidate. By Lemma 2.6, any minimum-cost,
crossing-free solution for
is a minimal
candidate. By Lemma 2.6, any minimum-cost,
crossing-free solution for ![]() is greedy on the interval
is greedy on the interval ![]() .
Hence, it will suffice to let
.
Hence, it will suffice to let ![]() be the matching problem
obtained from
be the matching problem
obtained from ![]() by discarding the nodes
by discarding the nodes
![]() and
prove that any minimum-cost, crossing-free solution for
and
prove that any minimum-cost, crossing-free solution for ![]() is
greedy on
is
greedy on ![]() . If
. If ![]() , there is nothing to prove,
so we assume
, there is nothing to prove,
so we assume ![]() . Note that
. Note that ![]() is now the
is now the ![]() -st node in
the
-st node in
the ![]() tour order. We use
tour order. We use
![]() to denote the
to denote the
![]() function for
function for ![]() .
.
We claim:
![]()
Claim (i) is immediate from the definition of
![]() . The intuitive
meaning of (ii) is that the benefit of using the jumper
. The intuitive
meaning of (ii) is that the benefit of using the jumper
![]() is reduced by the benefit already obtained from the jumper
is reduced by the benefit already obtained from the jumper
![]() . We formally prove (ii) for the case that
. We formally prove (ii) for the case that ![]() and
and ![]() are
red and
are
red and ![]() is blue, the opposite colored case has a similar proof.
Assume
is blue, the opposite colored case has a similar proof.
Assume ![]() ,
, ![]() and
and ![]() . Then
. Then
![\begin{eqnarray*}
\mbox{\sf Bnft}^\prime[R_a,B_c] &= & \sum_{\ell\in[a,b)}c_i + ...
...ll\in[b,c] }c_i
- \sum_{\ell\in[b,c)}c_i^\prime
- c(R_b,B_c)
\end{eqnarray*}](img193.gif)
Now let
![]() . By
Claim (ii),
. By
Claim (ii),
![]() ; since
; since ![]() ,
,
![]() . Likewise,
. Likewise,
![]() . Thus, by the induction hypothesis, any minimum-cost
solution for
. Thus, by the induction hypothesis, any minimum-cost
solution for ![]() is greedy on
is greedy on ![]() and
Lemma 2.8 is proved.
and
Lemma 2.8 is proved.![]()
![\begin{definition}
The $\Delta$\ function is defined by:
\begin{eqnarray*}
\Del...
...n[a,b)}c_\ell^\prime - \sum_{\ell\in(a,b]}c_\ell
\end{eqnarray*}\end{definition}](img198.gif)
![\begin{lemma}
\mbox{\relax}
\begin{romannum}
\item
$\mbox{\sf Bnft}[R_a,B_c]...
... and only if
$c(B_a,R_c)-c(B_b,R_c)<\Delta[B_a,B_b]$.
\end{romannum}\end{lemma}](img199.gif)
Lemma 2.10 follows immediately from the definitions.
![\begin{lemma}
Let $u,v,x,y$\ be in tour order with nodes $u$~and~$v$\ of
one col...
...htarrow~~ \mbox{\sf Bnft}[u,y]>\mbox{\sf Bnft}[v,y]
\end{displaymath}\end{lemma}](img200.gif)
proof: By Lemma 2.10,
![]() is equivalent to
is equivalent to
![]() , and
, and
![]() is equivalent
to
is equivalent
to
![]() . Now, by quasi-convexity,
. Now, by quasi-convexity,
![]() , which suffices to prove the lemma.
, which suffices to prove the lemma.![]()
Let ![]() and
and ![]() be distinct red nodes. The previous two lemmas
show that if there is any node
be distinct red nodes. The previous two lemmas
show that if there is any node ![]() (with
(with ![]() ,
, ![]() and
and ![]() in
tour order) such that
in
tour order) such that
![]() is greater than
is greater than
![]() , then the first such
, then the first such ![]() is the
is the
![]() -crossover point of
-crossover point of ![]() and
and ![]() . We shall denote
this first
. We shall denote
this first ![]() , if it exists, by
, if it exists, by ![]() ; if it does not
exist, then
; if it does not
exist, then ![]() is said to be undefined. Similarly,
is said to be undefined. Similarly,
![]() is defined to the be the
is defined to the be the
![]() -crossover
point of
-crossover
point of ![]() and
and ![]() , and, if defined, is the first
, and, if defined, is the first ![]() where
where
![]() is greater than
is greater than
![]() .
.
We now assume that we have a procedure ![]() , which given
nodes
, which given
nodes ![]() ,
, ![]() ,
, ![]() in tour order returns ``True'' if
in tour order returns ``True'' if
![]() and returns ``False'' if
and returns ``False'' if
![]() . (If neither condition holds, then
. (If neither condition holds, then
![]() may return an arbitrary truth value.) If the weak
analyticity condition holds, then
may return an arbitrary truth value.) If the weak
analyticity condition holds, then ![]() is constant time
computable. Without this assumption,
is constant time
computable. Without this assumption, ![]() is
is ![]() time
computable since Lemma 2.11 allows
time
computable since Lemma 2.11 allows ![]() to be
computable by binary search.
to be
computable by binary search.
The general idea of the algorithm given in section 3 below is that it
will scan the nodes in tour order searching for candidates. Whenever
a node is reached that is the head of candidate, the algorithm will
take the candidate specified in Lemma 2.8 (the one
that was denoted
![]() ) and greedily match the nodes in its
interior. The greedily matched nodes are then dropped from
consideration and the algorithm resumes its search for a candidate.
Suppose the
) and greedily match the nodes in its
interior. The greedily matched nodes are then dropped from
consideration and the algorithm resumes its search for a candidate.
Suppose the ![]() and
and ![]() are two nodes already scanned in this process
that are being remembered as potential endpoints of candidates.
Lemma 2.10 tells us that if a node
are two nodes already scanned in this process
that are being remembered as potential endpoints of candidates.
Lemma 2.10 tells us that if a node ![]() is found where
is found where
![]() , then at all succeeding nodes
, then at all succeeding nodes ![]() ,
,
![]() . By the criterion of
Lemma 2.8, this means that after the node
. By the criterion of
Lemma 2.8, this means that after the node ![]() is
found, there is no further reason to consider candidates that begin at
node
is
found, there is no further reason to consider candidates that begin at
node ![]() , since any candidate
, since any candidate
![]() would be subsumed by the better
candidate
would be subsumed by the better
candidate
![]() .
.
To conclude this section we describe the algorithm in very general
terms; in section 3 we give the precise specification of the
algorithm. The algorithm scans nodes (starting with node ![]() , say)
and maintains three lists. The first list,
, say)
and maintains three lists. The first list, ![]() , contains the
nodes in tour order which have been examined so far. The second list,
, contains the
nodes in tour order which have been examined so far. The second list,
![]() , contains all the red nodes that need to be considered as
potential endpoints of candidates (so
, contains all the red nodes that need to be considered as
potential endpoints of candidates (so
![]() is guaranteed to contain
all the nodes satisfying the criterion of
Lemma 2.8). The third list,
is guaranteed to contain
all the nodes satisfying the criterion of
Lemma 2.8). The third list,
![]() , similarly
contains all the blue nodes that need to be considered as potential
endpoints of candidates. At any point during the scan, the lists will
be of the form:
, similarly
contains all the blue nodes that need to be considered as potential
endpoints of candidates. At any point during the scan, the lists will
be of the form:
![\begin{eqnarray*}
{\cal M} & =& x_1,\ldots,x_{r-1} \\ [1ex]
{\mbox{\AMSeusm L}...
..._p} \\ [1ex]
{\mbox{\AMSeusm L}^1} & = & B_{b_1},\ldots,B_{b_q}
\end{eqnarray*}](img233.gif)

When scanning the next node ![]() , the algorithm must do the following
(we assume
, the algorithm must do the following
(we assume ![]() is blue, similar actions are taken for red nodes):
is blue, similar actions are taken for red nodes):
Step (![]() ) is justified by recalling that if
) is justified by recalling that if ![]() is past
is past
![]() , then
, then ![]() may be removed from
consideration as an endpoint of a candidate (by
Lemma 2.8).
may be removed from
consideration as an endpoint of a candidate (by
Lemma 2.8).
Step (![]() ) is justified as follows: suppose
) is justified as follows: suppose
![]() equals or precedes
equals or precedes
![]() (using tour order, beginning at
(using tour order, beginning at ![]() ).
Then at any future candidate endpoint
).
Then at any future candidate endpoint ![]() , either
, either ![]() follows or
equals
follows or
equals ![]() , in which case
, in which case
![]() is greater than
is greater than
![]() , or
, or ![]() precedes
precedes ![]() , in which case,
, in which case,
![]() is greater than
is greater than
![]() . Thus
. Thus
![]() will never be the starting endpoint of a candidate
satisfying the criteria of Lemma 2.8, and we may
drop it from consideration.
will never be the starting endpoint of a candidate
satisfying the criteria of Lemma 2.8, and we may
drop it from consideration.
To justify Step (![]() ) we must show that the candidate
) we must show that the candidate
![]() satisfies the criteria from Lemma 2.8: in view
of the correctness of the rest of the algorithm, for this it will
suffice to show that
satisfies the criteria from Lemma 2.8: in view
of the correctness of the rest of the algorithm, for this it will
suffice to show that
![]() for
all
for
all ![]() . For this, note that Step (
. For this, note that Step (![]() ) and condition (iii)
above ensure that
) and condition (iii)
above ensure that ![]() precedes
precedes
![]() for all
for all
![]() . This, in turn, implies
. This, in turn, implies
![]() for all
for all ![]() , which
proves the desired inequality.
, which
proves the desired inequality.
After the algorithm has scanned all the nodes once, it will have found
and processed all candidates
![]() where
where ![]() . However, since
the tour is circular, it is necessary to process candidates
. However, since
the tour is circular, it is necessary to process candidates
![]() with
with ![]() . At the end of the first scan, the list
. At the end of the first scan, the list ![]() consists of all nodes,
consists of all nodes,
![]() which have not been matched
yet and
which have not been matched
yet and
![]() and
and
![]() contain nodes
contain nodes
![]() and
and
![]() , as usual. During the second scan, the
algorithm is searching for any candidates of the form
, as usual. During the second scan, the
algorithm is searching for any candidates of the form
![]() with
with ![]() or of the form
or of the form
![]() with
with ![]() (and only
for such candidates). To process a node during the second scan, the
algorithm pops
(and only
for such candidates). To process a node during the second scan, the
algorithm pops ![]() off the left end of
off the left end of ![]() , implicitly renames
, implicitly renames
![]() to
to ![]() and the rest of the nodes
and the rest of the nodes ![]() to
to ![]() , sets
, sets
![]() , does Step (
, does Step (![]() ): (still assuming
): (still assuming ![]() is blue)
is blue)
The second scan will stop as soon as both ![]() lists become empty.
At this point no candidates remain and a greedy matching may be used
for the remaining nodes in the
lists become empty.
At this point no candidates remain and a greedy matching may be used
for the remaining nodes in the ![]() list.
list.
The actual description of the algorithm with an efficient
implementation is given in section 3, and it is there proved that the
algorithm is linear time with the weak analyticity condition and
![]() time otherwise. Although we described steps
(
time otherwise. Although we described steps
(![]() )-(
)-(![]() ) only for blue
) only for blue ![]() above, the algorithm in
section 3 uses a toggle
above, the algorithm in
section 3 uses a toggle ![]() to handle both colors with the same
code. Finally, one more important feature of the algorithm is the way
in which it computes the values of the
to handle both colors with the same
code. Finally, one more important feature of the algorithm is the way
in which it computes the values of the
![]() function and of the
function and of the
![]() function: it uses intermediate values
function: it uses intermediate values ![]() which are
defined as follows.
which are
defined as follows.
![\begin{definition}
The $I[x]$\ function is defined by
\begin{eqnarray*}
I[R_a] &...
...
\end{eqnarray*}Note that $I[R_{a+1}] = I[B_a]-c(B_a,R_{a+1})$.
\end{definition}](img279.gif)
It is immediate from the definitions that, if ![]() are tour order (starting
from
are tour order (starting
from ![]() ), then
), then
![\begin{eqnarray*}
\Delta[x,y] &=& I[y]-I[x] \qquad\qquad\qquad \mbox{\rm for $x$...
...& I[x]-I[y]-c(x,y) \qquad \mbox{\rm for $x$\ blue, $y$\ red.}\\
\end{eqnarray*}](img280.gif)
These equalities permit the values of ![]() and
and
![]() to be
computed in constant time from the values of
to be
computed in constant time from the values of ![]() . Also, it is
important to note that only the relative
. Also, it is
important to note that only the relative ![]() values are needed; in
other words, it is OK if the
values are needed; in
other words, it is OK if the ![]() values are shifted by a constant
additive constant, since we always use the difference between two
values are shifted by a constant
additive constant, since we always use the difference between two
![]() values.
values.
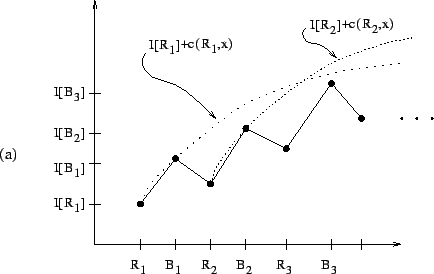
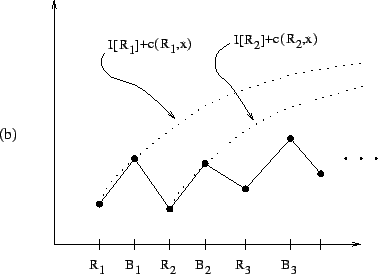
The ![]() function is not only easy to compute, but also provides
an intuitive graphical means of understanding the above lemmas and
algorithm description. For example, in Figure 2.1,
function is not only easy to compute, but also provides
an intuitive graphical means of understanding the above lemmas and
algorithm description. For example, in Figure 2.1,
![]() is a (minimal) candidate whereas
is a (minimal) candidate whereas
![]() and
and
![]() are not candidates. In Figure 2.2(a), the node
are not candidates. In Figure 2.2(a), the node ![]() is the relative crossover,
is the relative crossover, ![]() , of
, of ![]() and
and ![]() ; on the other
hand, in Figure 2.2(b), the relative crossover does not exist.
Figure 2.3(a) shows an example where
; on the other
hand, in Figure 2.2(b), the relative crossover does not exist.
Figure 2.3(a) shows an example where
![]() is true and Figure 2.3(b) shows an example
where
is true and Figure 2.3(b) shows an example
where
![]() is false.
is false.
|
proof: By symmetry, it will suffice to prove part (i). Since the lemma is
trivial in case ![]() , we assume
, we assume ![]() . Let
. Let ![]() be a
crossing-free minimum-cost matching: we must prove that
be a
crossing-free minimum-cost matching: we must prove that ![]() is
greedy on
is
greedy on ![]() . By the crossing-freeness of
. By the crossing-freeness of ![]() and by
the fact that
and by
the fact that
![]() is a minimal candidate,
is a minimal candidate, ![]() does
not contain any jumper with both endpoints in
does
not contain any jumper with both endpoints in ![]() , except
possibly
, except
possibly
![]() itself. If
itself. If
![]() is in
is in ![]() , then
the same reasoning shows that
, then
the same reasoning shows that ![]() is greedy on
is greedy on ![]() ; so we
suppose that
; so we
suppose that
![]() is not in
is not in ![]() . Since we are dealing
(with no loss of generality) with balanced tours, we may assume that
. Since we are dealing
(with no loss of generality) with balanced tours, we may assume that
![]() , by renumbering nodes if necessary.
, by renumbering nodes if necessary.
Claim (i):
![]() is not in
is not in ![]() .
.
Suppose, for a contradiction, that
![]() is in
is in ![]() .
Let
.
Let ![]() be the least value such that
be the least value such that
![]() is in
is in ![]() for some
for some ![]() . Note that such a
. Note that such a ![]() ,
, ![]() , must exist since
there are no jumpers in
, must exist since
there are no jumpers in ![]() and since
and since ![]() is not
greedy on
is not
greedy on ![]() (it can not be greedy on
(it can not be greedy on ![]() , since
, since
![]() is a candidate). By choice of
is a candidate). By choice of ![]() ,
, ![]() is greedy on
is greedy on
![]() .
These edges in the matching
.
These edges in the matching ![]() are represented by edges
drawn above the line in Figure 3.1(a).
Since
are represented by edges
drawn above the line in Figure 3.1(a).
Since
![]() is a minimal candidate,
is a minimal candidate,
![]() , so Lemma 2.10 implies
, so Lemma 2.10 implies
Claim (ii):
![]() is not in
is not in ![]() .
.
Claim (ii) is proved by an argument similar to Claim (i). Alternatively,
reverse the colors and the tour order and Claim (ii) is a version
of Claim (i).
Claim (iii):
The matching ![]() is greedy on
is greedy on ![]() .
.
Suppose, for a contradiction that ![]() is not greedy
on
is not greedy
on ![]() .
In view of Claims (i) and (ii) and since
.
In view of Claims (i) and (ii) and since ![]() has no jumpers
in
has no jumpers
in ![]() , this means that there exist
, this means that there exist ![]() and
and ![]() such
that
such
that ![]() is the least value
such that
is the least value
such that ![]() contains
contains
![]() with
with ![]() and
and ![]() is the least value such that
is the least value such that ![]() contains
contains
![]() with
with ![]() .
Namely, let
.
Namely, let ![]() be the least value
be the least value ![]() such that
such that
![]() is not
in
is not
in ![]() and
and ![]() be the least value
be the least value ![]() such that
such that
![]() is not
in
is not
in ![]() . For these choices of
. For these choices of ![]() and
and ![]() , it must be
that
, it must be
that
![]() and that
and that ![]() is greedy
on
is greedy
on ![]() and on
and on
![]() .
These edges in the matching
.
These edges in the matching ![]() are represented by edges
drawn above the line in Figure 3.1(b).
are represented by edges
drawn above the line in Figure 3.1(b).
Since
![]() is a candidate,
is a candidate,
In this section, we give the actual algorithm for the Main Theorems. The correctness of the algorithm follows from the development in section 2.2. With D. Robinson and K. Kanzelberger, we have developed efficient implementations in ANSI C of all the algorithms described below [5].7
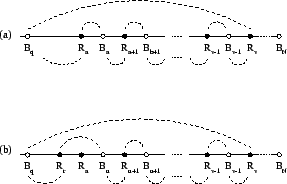
|
Subscripts ![]() ,
, ![]() , and
, and ![]() are used to select the rightmost item,
leftmost item, and the item preceding the rightmost, respectively. So
are used to select the rightmost item,
leftmost item, and the item preceding the rightmost, respectively. So
![]() refers to the leftmost element of
refers to the leftmost element of
![]() ,
,
![]() refers to the item just before the rightmost member of
refers to the item just before the rightmost member of ![]() , etc.
Each deque element is actually a pair, for example,
, etc.
Each deque element is actually a pair, for example,
![]() ; the first entry
; the first entry ![]() of the pair is a node and the second
entry
of the pair is a node and the second
entry ![]() is a numerical value, namely
is a numerical value, namely ![]() as defined in
section 2.2. To simplify notation, we shall use the same notation for
a deque element as for the node which is its first component. Thus,
as defined in
section 2.2. To simplify notation, we shall use the same notation for
a deque element as for the node which is its first component. Thus,
![]() also denotes the node which is its first component. We
write
also denotes the node which is its first component. We
write ![]() to denote its second (numerical) component.
Similar conventions apply to the
to denote its second (numerical) component.
Similar conventions apply to the
![]() deques. To simplify
our presentation of the algorithm we deal with boundary effects by
augmenting the definition of primitive operations as necessary. For
example, accessing a non-existent deque element will return an undefined indicator
deques. To simplify
our presentation of the algorithm we deal with boundary effects by
augmenting the definition of primitive operations as necessary. For
example, accessing a non-existent deque element will return an undefined indicator ![]() and, in general, functions of
undefined operands are false or zero (in particular, the cost function
and, in general, functions of
undefined operands are false or zero (in particular, the cost function
![]() and the
and the ![]() functions return zero if they have
functions return zero if they have ![]() as an argument).
as an argument).
Function Input() returns the next vertex from an imagined input tape
which moves in the forward direction only; and is assumed to hold a
balanced, alternating color tour. When the tape's end is reached,
`undefined' is returned. Procedure Output() is used to write an
individual matching to an imagined output tape. They are written as
discovered; but can easily be output in tour order (with only an extra
![]() -time computation).
-time computation).
To use the same code for red nodes and blue nodes, a variable ![]() tracks vertex color by toggling between
tracks vertex color by toggling between ![]() and
and ![]() . Our convention
is that
. Our convention
is that ![]() corresponds to blue, and
corresponds to blue, and ![]() to red.
to red.
The algorithm first reads nodes from the input and pushes them onto
the right end of the ![]() -deque, and then twice scans the nodes in
tour order. During the two scans, nodes are popped from the left end
of
-deque, and then twice scans the nodes in
tour order. During the two scans, nodes are popped from the left end
of ![]() and then pushed onto its right end.8 In addition, while processing a node, some
nodes may be popped off the right end of
and then pushed onto its right end.8 In addition, while processing a node, some
nodes may be popped off the right end of ![]() to be matched. It
will always be the case that
to be matched. It
will always be the case that ![]() contains a sequence of contiguous
nodes in tour order and that the node currently being scanned
immediately follows the (formerly) rightmost element of
contains a sequence of contiguous
nodes in tour order and that the node currently being scanned
immediately follows the (formerly) rightmost element of ![]() .
.
The variable ![]() will be maintained as a color toggle, so that
will be maintained as a color toggle, so that
![]() is equal to
is equal to ![]() if the node currently being processed is red
and to
if the node currently being processed is red
and to ![]() if the current node is blue. The algorithm used for
pushing an element onto the right end of
if the current node is blue. The algorithm used for
pushing an element onto the right end of ![]() is:
is:
![]()
Algorithm 3.1 merely computes the ![]() value for a node
value for a node ![]() and pushes the node and its
and pushes the node and its ![]() value on the right end of
value on the right end of ![]() . To
justify the computation of the value of
. To
justify the computation of the value of ![]() , note that if
, note that if ![]() is
blue, then
is
blue, then ![]() and
and ![]() was defined to equal
was defined to equal
![]() ; whereas, if
; whereas, if ![]() is red then
is red then ![]() and
and ![]() equals
equals
![]() . (Unless
. (Unless ![]() is empty, in which case,
is empty, in which case,
![]() .)
.)
Once the current node has been pushed onto the right end of ![]() ,
the following code implements Step (
,
the following code implements Step (![]() ) from section 2.2:
) from section 2.2:
![]()
To justify the correctness of the while condition, suppose that the
currently scanned node is red, so ![]() . By
Lemma 2.10,
. By
Lemma 2.10,
![]() iff
iff
![]() .
Furthermore,
.
Furthermore,
![]() is equal to
is equal to
![]() since
since
![]() contains blue
nodes and
contains blue
nodes and ![]() (by the equalities at the end of section 2.2). In
this case,
(by the equalities at the end of section 2.2). In
this case, ![]() is past the crossover point of
is past the crossover point of
![]() and
and
![]() , so
, so
![]() may be discarded from
consideration as a left endpoint of a candidate. A similar
calculation justifies the case when the current node is blue.
may be discarded from
consideration as a left endpoint of a candidate. A similar
calculation justifies the case when the current node is blue.
To implement Step (![]() ), the following code is used:
), the following code is used:
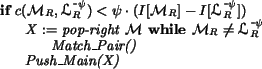
where Match_Pair is defined below. The above if statement
checks whether
![]() is a candidate; if so, the algorithm
greedily assigns edges to node in the interior of the candidate (where
`greedily' means with respect to the nodes that have not already been
assigned). Before the greedy assignment is started, the rightmost
entry is popped from
is a candidate; if so, the algorithm
greedily assigns edges to node in the interior of the candidate (where
`greedily' means with respect to the nodes that have not already been
assigned). Before the greedy assignment is started, the rightmost
entry is popped from ![]() and is saved as
and is saved as ![]() to pushed back on the
right end afterwards. There are two reasons for this: firstly, this
gets the current node
to pushed back on the
right end afterwards. There are two reasons for this: firstly, this
gets the current node ![]() out of the way of Match_Pair's operation,
and secondly and more importantly, when
out of the way of Match_Pair's operation,
and secondly and more importantly, when ![]() is pushed back
onto
is pushed back
onto ![]() , the
, the ![]() value for the current node is recomputed so
as to be correct for the reduced matching problem in which the
greedily matched nodes are no longer present. Match_Pair is the
following procedure:
value for the current node is recomputed so
as to be correct for the reduced matching problem in which the
greedily matched nodes are no longer present. Match_Pair is the
following procedure:
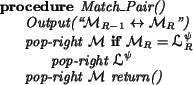
The procedure Match_Pair assigns a jumper
![]() and
discards a matched node from the deque
and
discards a matched node from the deque
![]() if it appears there.
Because of the while condition controlling calls to
Match_Pair,
it is not possible for a matched node
to occur in
if it appears there.
Because of the while condition controlling calls to
Match_Pair,
it is not possible for a matched node
to occur in
![]() , so we do not check for this condition.
, so we do not check for this condition.
To implement Step (![]() ), the following code is used:
), the following code is used:
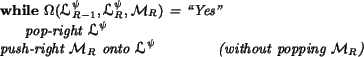
That completes the description of the how nodes are processed during
the first scan. As mentioned earlier, the last instruction (the push-right) is omitted from Step (![]() ) during the second scan.
Other than this, the processing for Steps (
) during the second scan.
Other than this, the processing for Steps (![]() )-(
)-(![]() ) is
identical in the two scans.
) is
identical in the two scans.
One potentially confusing aspect of the second scan is that the ![]() values are no longer actually the correct
values are no longer actually the correct ![]() values: for example,
it is no longer the case that
values: for example,
it is no longer the case that ![]() is necessarily equal to
zero. Strictly speaking, the
is necessarily equal to
zero. Strictly speaking, the ![]() values all shift by an additive
constant when an entry is popped from the left end of
values all shift by an additive
constant when an entry is popped from the left end of ![]() ;
however, it is not necessary to implement this shift, since the
algorithm only uses differences between
;
however, it is not necessary to implement this shift, since the
algorithm only uses differences between ![]() values. The end result
is that nothing special needs to be done to the
values. The end result
is that nothing special needs to be done to the ![]() values when we
pop-left
values when we
pop-left ![]() .
.
After both scans are completed, any remaining nodes may be greedily matched. As discussed above, there are two possible greedy matchings and both have the same (optimal) cost. Thus either one may be used: the algorithm below just calls Match_Pair repeatedly to assign one of these greedy matchings.
The complete matching algorithm is shown as Algorithm 3.2.
When interpreting Algorithm 3.2, it is necessary to recall our
conventions that any predicate of undefined arguments is to be false.
This situation can occur in the four while and if
conditions of Process_Node. If
![]() is empty, then
is empty, then
![]() is
undefined and the two while conditions and the first if
condition are to be false. Similarly, if
is
undefined and the two while conditions and the first if
condition are to be false. Similarly, if
![]() has
has ![]() elements,
then the first while condition is to be false; and if
elements,
then the first while condition is to be false; and if
![]() has
has
![]() elements, then the final while condition is to be false.
elements, then the final while condition is to be false.
The runtime of Algorithm 3.2 is either ![]() or
or ![]() depending
on whether the weak analyticity condition holds. To see this, note
that the initialization and the windup processing both take
depending
on whether the weak analyticity condition holds. To see this, note
that the initialization and the windup processing both take ![]() time. The loops for the each of the two scans are executed
time. The loops for the each of the two scans are executed ![]() times. Except for the while loops, each call to Process_Node
takes constant time. The second while loop (which calls
Match_Pair) is executed more than once only when edges are being
output. If the first or third while loop is executed more than
once, then vertices are being popped from the
times. Except for the while loops, each call to Process_Node
takes constant time. The second while loop (which calls
Match_Pair) is executed more than once only when edges are being
output. If the first or third while loop is executed more than
once, then vertices are being popped from the ![]() stacks.
Since
stacks.
Since
![]() edges are output and since
edges are output and since ![]() vertices are
pushed onto the
vertices are
pushed onto the ![]() stacks, each of these while loops
are executed only
stacks, each of these while loops
are executed only ![]() times during the entire execution of
the algorithm. An iteration of the first or second while loop
takes constant time, while an iteration of the third while loop
takes either constant time or
times during the entire execution of
the algorithm. An iteration of the first or second while loop
takes constant time, while an iteration of the third while loop
takes either constant time or ![]() time, depending on whether
the weak analyticity property holds.
time, depending on whether
the weak analyticity property holds.
When the weak analyticity condition holds, the ![]() predicate
typically operates in constant time by computing two theoretical
relative crossovers and comparing their positions. This happen, for
example, when the tour consists of points lying a circle, with the
cost function equal to Euclidean distance; section 3.3 outlines a
constant-time algorithm for this example. Without the weak
analyticity condition, the
predicate
typically operates in constant time by computing two theoretical
relative crossovers and comparing their positions. This happen, for
example, when the tour consists of points lying a circle, with the
cost function equal to Euclidean distance; section 3.3 outlines a
constant-time algorithm for this example. Without the weak
analyticity condition, the ![]() -predicate runs in logarithmic
time, by using a binary search of the
-predicate runs in logarithmic
time, by using a binary search of the ![]() -deque. This general
(not weakly analytic) case is handled by the generic
-deque. This general
(not weakly analytic) case is handled by the generic ![]() algorithm discussed in section 3.3.
algorithm discussed in section 3.3.
There are a couple of improvements that can be made to the algorithm
which will increase execution speed by a constant factor. Firstly,
the calls to Match_Pair made during the ``Windup Processing'' do not
need to check if
![]() , since
, since
![]() is empty at this time.
Secondly, if computing the cost function
is empty at this time.
Secondly, if computing the cost function ![]() is more costly than
simple addition, then it is possible for Push_Main() to use an
alternative method during the two scans to compute the cost
is more costly than
simple addition, then it is possible for Push_Main() to use an
alternative method during the two scans to compute the cost
![]() for nodes
for nodes ![]() which have just been popped from the left
of
which have just been popped from the left
of ![]() (except for the first one popped from the left in the first
scan). Namely, the algorithm can save the old
(except for the first one popped from the left in the first
scan). Namely, the algorithm can save the old ![]() value for the
node
value for the
node ![]() as it is left-popped off the deque
as it is left-popped off the deque ![]() . Then the cost
function can be computed by computing the difference between the
. Then the cost
function can be computed by computing the difference between the
![]() value of
value of ![]() and the
and the ![]() of the previous node left-popped
from
of the previous node left-popped
from ![]() . This second improvement applies only to the first
Push_Main call in Process_Node.
. This second improvement applies only to the first
Push_Main call in Process_Node.
During the first scan, the procedure ![]() is called (repeatedly)
by Process_Node to determine whether
is called (repeatedly)
by Process_Node to determine whether
![]() should be
popped before the current node
should be
popped before the current node ![]() is pushed onto the right
end of the
is pushed onto the right
end of the
![]() -deque. During the second scan,
-deque. During the second scan, ![]() is never
pushed onto the
is never
pushed onto the
![]() -deque; however, using the procedure
-deque; however, using the procedure ![]() can
allow the
can
allow the
![]() -deque to be more quickly emptied, thus speeding up the
algorithm's execution. (However, the use of the
-deque to be more quickly emptied, thus speeding up the
algorithm's execution. (However, the use of the ![]() could be
omitted during the second scan, without affecting the correctness of
the algorithm.)
could be
omitted during the second scan, without affecting the correctness of
the algorithm.)
When ![]() is called,
is called,
![]() ,
,
![]() and
and ![]() are
distinct nodes, in tour order, and of the same color. Let
are
distinct nodes, in tour order, and of the same color. Let
![]() and
and
![]() . Let
. Let ![]() denote the
denote the
![]() -crossover point of
-crossover point of
![]() and
and
![]() , and let
, and let ![]() denote the
denote the ![]() -crossover point of
-crossover point of
![]() and
and ![]() (note
(note ![]() and/or
and/or ![]() may not exist). By definition,
may not exist). By definition, ![]() and
and ![]() are
both opposite in color from the other three nodes. The
procedure
are
both opposite in color from the other three nodes. The
procedure ![]() must return True if
must return True if ![]() exists and
exists and ![]() does
not, must return False if
does
not, must return False if ![]() does not exist, and, if both
exist, must return True if
does not exist, and, if both
exist, must return True if
![]() are in tour order,
must return True if
are in tour order,
must return True if
![]() are in tour order, and may
return either value if
are in tour order, and may
return either value if ![]() .
.
In this section, we discuss two algorithms for ![]() . We first
discuss a ``generic'' algorithm that works for any cost function,
regardless of whether the weak analyticity condition holds. This
generic
. We first
discuss a ``generic'' algorithm that works for any cost function,
regardless of whether the weak analyticity condition holds. This
generic ![]() procedure is shown as Algorithm 3.3 below. The
generic
procedure is shown as Algorithm 3.3 below. The
generic ![]() executes a binary search for a node which is at or
past one of the crossover points, but is not at or past the other.
Obviously, if the crossover
executes a binary search for a node which is at or
past one of the crossover points, but is not at or past the other.
Obviously, if the crossover ![]() exists, then it exists in the range
exists, then it exists in the range
![]() , and if the crossover
, and if the crossover ![]() exists, it is in the
range
exists, it is in the
range
![]() . Furthermore,
. Furthermore, ![]() can not exist in the
range
can not exist in the
range
![]() , since otherwise it would have been
popped when
, since otherwise it would have been
popped when ![]() was reached (by the first while loop in an
earlier call to Match_Pair). Hence, the binary search may be
confined to the range
was reached (by the first while loop in an
earlier call to Match_Pair). Hence, the binary search may be
confined to the range
![]() , provided that True is returned in the event that the binary search is unsuccessful.
, provided that True is returned in the event that the binary search is unsuccessful.
In Algorithm 3.3, a new notation ![]() is used -- this presumes
that the
is used -- this presumes
that the ![]() deque is implemented as an array, the elements
of
deque is implemented as an array, the elements
of ![]() fill a contiguous block of the array elements. When we
write
fill a contiguous block of the array elements. When we
write ![]() , we mean the
, we mean the ![]() -th entry of the array. The
-th entry of the array. The ![]() deques can contain pointers to
deques can contain pointers to ![]() deque entries; in fact, in
our preferred implementation, the
deque entries; in fact, in
our preferred implementation, the ![]() deque entries contain
only a index for an
deque entries contain
only a index for an ![]() deque entry. Thus the value
deque entry. Thus the value ![]() can be
found in constant time for Algorithm 3.3.
can be
found in constant time for Algorithm 3.3.
The generic ![]() algorithm shown in Algorithm 3.3 takes
algorithm shown in Algorithm 3.3 takes ![]() time since it uses a binary search.
time since it uses a binary search.
Next we describe an example of a linear time algorithm for ![]() where the weak analyticity condition holds. For this example,
we assume that the nodes of the quasiconvex tour lie on the
unit circle in the
where the weak analyticity condition holds. For this example,
we assume that the nodes of the quasiconvex tour lie on the
unit circle in the ![]() plane, the cost function
is equal to straight-line Euclidean distance,
and the tour proceeds in counterclockwise
order around the circle.
The
plane, the cost function
is equal to straight-line Euclidean distance,
and the tour proceeds in counterclockwise
order around the circle.
The ![]() algorithm either is given, or computes, the
algorithm either is given, or computes, the ![]() coordinates of the three nodes
coordinates of the three nodes
![]() ,
,
![]() and
and ![]() .
It then uses a routine Circle_Crossover to find the theoretical
.
It then uses a routine Circle_Crossover to find the theoretical
![]() -crossover
-crossover ![]() of
of
![]() and
and
![]() and, the
theoretical
and, the
theoretical ![]() -crossover of
-crossover of
![]() and
and ![]() .
If the theoretical crossover
.
If the theoretical crossover ![]() exists, it will be in the
interval
exists, it will be in the
interval
![]() , and if
, and if ![]() exists,
exists, ![]() will be
in the interval
will be
in the interval
![]() . When
. When ![]() and
and ![]() both exist,
the
both exist,
the ![]() procedure returns True if
procedure returns True if
![]() are in
tour order or any two of these nodes are equal; and otherwise returns
False.
are in
tour order or any two of these nodes are equal; and otherwise returns
False.
Of course, the crucial implementation difficulty for the procedure ![]() is the algorithm for Circle_Crossover: this is shown as Algorithm 3.4.
Circle_Crossover takes two points
is the algorithm for Circle_Crossover: this is shown as Algorithm 3.4.
Circle_Crossover takes two points ![]() and
and ![]() lying
on the unit circle in the
lying
on the unit circle in the ![]() -plane and a real value
-plane and a real value ![]() . The
theoretical
. The
theoretical ![]() -crossover point of
-crossover point of ![]() and
and ![]() is
found as an intersection point of the unit circle and the hyperbola
consisting of those points which have distance from
is
found as an intersection point of the unit circle and the hyperbola
consisting of those points which have distance from ![]() equal
to
equal
to ![]() plus their distance from
plus their distance from ![]() (namely, the intersection
which is not between
(namely, the intersection
which is not between ![]() and
and ![]() in tour order.)
Letting the `half inner product',
in tour order.)
Letting the `half inner product', ![]() , equal
, equal
![]() ,
the distance between the two point is equal to
,
the distance between the two point is equal to ![]() , where
, where
![]() . And, the midpoint of the line segment between
the two points is distance
. And, the midpoint of the line segment between
the two points is distance
![]() from the origin.
To conveniently express the equation for the hyperbola, we
set up
from the origin.
To conveniently express the equation for the hyperbola, we
set up ![]() -axes as a rigid translation of the
-axes as a rigid translation of the ![]() axes, positioned
so that the points
axes, positioned
so that the points ![]() and
and ![]() have
have ![]() -coordinates
-coordinates
![]() and
and ![]() , respectively. This makes the origin have
, respectively. This makes the origin have
![]() -coordinates
-coordinates ![]() , where
, where
![]() with
the sign being
with
the sign being ![]() iff the angle from
iff the angle from ![]() to
to ![]() is
is
![]() . In the
. In the ![]() -plane, the hyperbola has equation
-plane, the hyperbola has equation
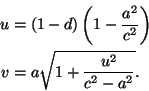
An efficient and highly portable ANSI-C implementation of our
algorithms is described in [5], which
includes complete source
code, test programs for several interesting cases, benchmark results,
and software to produce postscript graphical representations of the
matchings found.
To help ensure the correctness of our implementation,
a straightforward ![]() dynamic programming
solution was also implemented, and the results compared for 4,000,000
pseudo-randomly drawn problems. Figure 1.1 shows an
example of a matching produced by our software.
dynamic programming
solution was also implemented, and the results compared for 4,000,000
pseudo-randomly drawn problems. Figure 1.1 shows an
example of a matching produced by our software.
Benchmark results for a variety of RISC processors produced nearly
identical results when normalized by clock rate. So timing results
in [5]
are given in units of RISC cycles. Graphs of up to ![]() nodes are included in this study.
nodes are included in this study.
Recall that ![]() time is a worst case bound for generic
time is a worst case bound for generic
![]() . One interesting experimental result is that over the range
of graph sizes considered, and for the specific settings implemented
in the test programs, and given the uniform pseudo-random manner in
which problem instances were generated, the generic
. One interesting experimental result is that over the range
of graph sizes considered, and for the specific settings implemented
in the test programs, and given the uniform pseudo-random manner in
which problem instances were generated, the generic ![]() implementation exhibits very nearly linear-time performance. I.e., the
experimentally observed runtime of
implementation exhibits very nearly linear-time performance. I.e., the
experimentally observed runtime of ![]() was nearly constant.
We suspect that this
is primarily a consequence of the uniform random distribution
from which problems
were drawn, and that it should be possible to demonstrate
expected time results better than
was nearly constant.
We suspect that this
is primarily a consequence of the uniform random distribution
from which problems
were drawn, and that it should be possible to demonstrate
expected time results better than ![]() for more
structured settings.
for more
structured settings.
The benchmarks included one line-like and two circular settings.
Solving pseudo-randomly drawn matching problems of size ![]() , required
on average between
, required
on average between ![]() and
and ![]() RISC cycles per node --
depending on the setting, and on whether a constant time or generic
RISC cycles per node --
depending on the setting, and on whether a constant time or generic
![]() was employed. It is interesting to note, that in all cases,
the constant time
was employed. It is interesting to note, that in all cases,
the constant time ![]() performed better by a factor ranging from
roughly 1.5 to slightly over 3. Thus, for some problems, the linear
time result of this paper may be of practical interest.
performed better by a factor ranging from
roughly 1.5 to slightly over 3. Thus, for some problems, the linear
time result of this paper may be of practical interest.
Despite our focus on efficiency, further code improvements and cost function evaluation by table lookup, may contribute to significant performance improvement.
In this section we show how the earlier algorithms can be applied to non-bipartite, quasi-convex tours. The principal observation is that non-bipartite tours may be made bipartite by the simple construction of making the nodes alternate in color. This is already observed by Marcotte-Suri [20] in a more restrictive setting; we repeat the construction here for the sake of completeness.
First, it is apparent that the proof of Lemma 2.3 still
works in the non-bipartite case, and thus any non-bipartite, quasi-convex
tour has a minimum-cost matching in which no jumpers cross. This fact
implies the following two lemmas:
![]()
proof: It will suffice to show that any crossing-free matching has this property.
Suppose
![]() is a jumper in a crossing-free matching, with
is a jumper in a crossing-free matching, with ![]() .
Since
.
Since ![]() is
even, the matching is complete in that every node is matched.
The crossing free property thus implies that the nodes in
is
even, the matching is complete in that every node is matched.
The crossing free property thus implies that the nodes in ![]() are matched with each other; so there are an even number of such nodes,
i.e., one of
are matched with each other; so there are an even number of such nodes,
i.e., one of ![]() and
and ![]() is even and the other is odd.
is even and the other is odd. ![]()
proof: If ![]() is even then this lemma is just a special case of
the former lemma.
If
is even then this lemma is just a special case of
the former lemma.
If ![]() is odd, then add an additional node
is odd, then add an additional node ![]() to the end of
the tour, with
to the end of
the tour, with
![]() for all
for all ![]() . The resulting
tour is again quasi-convex and of even length; so the lemma again
follows immediately from the former lemma.
. The resulting
tour is again quasi-convex and of even length; so the lemma again
follows immediately from the former lemma. ![]()
When Lemmas 4.1 and 4.2 apply,
we may color the even nodes red and the odd nodes blue and reduce
the non-bipartite matching problem to a bipartite matching problem.
As an immediate corollary, we have that
the two Main Theorems also apply in the non-bipartite setting; namely,
for non-bipartite, quasi-convex tours of even length and for
non-bipartite, line-like, quasi-convex tours, the matching
problem can always be solved in ![]() time and it can be solved
in
time and it can be solved
in ![]() time if the weak analyticity condition holds.
time if the weak analyticity condition holds.
We do not know whether similar algorithms exist for the case of general (i.e., non-line-like) quasi-convex tours of odd length. Similarly, we do not know any linear or near-linear time algorithms for bipartite, quasi-convex tours which are neither balanced nor line-like.
We conclude this section by mentioning a tantalizing connection between
our work and the work of F. F. Yao[25]. Yao
gave a quadratic runtime algorithm for solving the
dynamic programming problem
As a final topic we briefly discuss the application of our matching
results to string comparison. A full treatment is beyond the scope of
this paper, but additional details and related algorithms may be found
in [6]. Given two symbol strings
![]() and
and
![]() , our goal is to measure a
particular notion of distance between them. Intuitively,
distance acts as a measure of similarity, i.e., strings that are
highly similar (highly dissimilar) are to have a small (large)
distance between them. The purpose of such formulations is usually to
approximate human similarity judgments within a pattern
classification or information retrieval system.
, our goal is to measure a
particular notion of distance between them. Intuitively,
distance acts as a measure of similarity, i.e., strings that are
highly similar (highly dissimilar) are to have a small (large)
distance between them. The purpose of such formulations is usually to
approximate human similarity judgments within a pattern
classification or information retrieval system.
Suppose ![]() is a monotonely increasing, concave-down function with
is a monotonely increasing, concave-down function with
![]() . Let symbols
. Let symbols
![]() in
in ![]() be a graph's red
nodes,
be a graph's red
nodes,
![]() in
in ![]() be its blue nodes, and consider
bipartite matchings of these
be its blue nodes, and consider
bipartite matchings of these ![]() symbols. In the simplest
formulation we define the cost of an edge
symbols. In the simplest
formulation we define the cost of an edge
![]() as
as ![]() if
if ![]() and
and ![]() are the same symbol, and as
are the same symbol, and as ![]() if
if ![]() and
and
![]() are distinct symbols. The cost of matching unequal characters
can also be set to be any other fixed value instead of
are distinct symbols. The cost of matching unequal characters
can also be set to be any other fixed value instead of ![]() . Our
distance,
. Our
distance, ![]() , between strings
, between strings ![]() and
and ![]() is then the
minimum cost of any such bipartite matching.
is then the
minimum cost of any such bipartite matching.
As an example, consider the two strings ``delve'' and ``level'' and
let ![]() . Then the distance between these two strings is
. Then the distance between these two strings is
![]() .
.
As we have set up our problem above, the computation of
![]() is not directly an instance of the quasi-convex matching
problem. However we can compute the
is not directly an instance of the quasi-convex matching
problem. However we can compute the ![]() function by considering
each alphabet symbol
function by considering
each alphabet symbol ![]() separately, and solving the quasi-convex
matching problem
separately, and solving the quasi-convex
matching problem ![]() which results from restricting
attention to occurrences of a single alphabet symbol at a time. To
make this clear, we introduce a special symbol ``-'' which indicates
the absence of an alphabet symbol.
The value of
which results from restricting
attention to occurrences of a single alphabet symbol at a time. To
make this clear, we introduce a special symbol ``-'' which indicates
the absence of an alphabet symbol.
The value of
![]() can be expressed as the sum
can be expressed as the sum
We will loosely refer to distance functions that result from this kind
of formulation as ![]() -distances. Assuming that
-distances. Assuming that ![]() satisfies
the weak analyticity condition, it is not too difficult to show that
it is possible to compute
satisfies
the weak analyticity condition, it is not too difficult to show that
it is possible to compute ![]() in linear time.
If the weak analyticity condition does not hold,
then our results give an
in linear time.
If the weak analyticity condition does not hold,
then our results give an ![]() time algorithm.
time algorithm.
A novel feature of our ![]() -distances is that distinct
alphabet symbols are treated independently. This is in contrast to
most prior work which has used `least edit distance' for string
comparison (see [21] for a survey). As an
illustration of the difference between our distance measure and the
`edit distance' approach, consider comparing the word ``abcde''
with its mirror image ``edcba''. Our approach recognizes some
similarity between these two forms, while the most standard `edit
distance' approach sees only that the two strings have ``c'' in
common -- in essence substituting the first two and last two symbols
of the string without noticing the additional occurrences of the same
symbols at the other end of the other string.
-distances is that distinct
alphabet symbols are treated independently. This is in contrast to
most prior work which has used `least edit distance' for string
comparison (see [21] for a survey). As an
illustration of the difference between our distance measure and the
`edit distance' approach, consider comparing the word ``abcde''
with its mirror image ``edcba''. Our approach recognizes some
similarity between these two forms, while the most standard `edit
distance' approach sees only that the two strings have ``c'' in
common -- in essence substituting the first two and last two symbols
of the string without noticing the additional occurrences of the same
symbols at the other end of the other string.
A special form of our ![]() -distance measure in which
-distance measure in which ![]() , and
the optimal matching is only approximated, was introduced earlier by
the authors and shown to have a simple linear time
algorithm [26,27]. Its
relationship to
, and
the optimal matching is only approximated, was introduced earlier by
the authors and shown to have a simple linear time
algorithm [26,27]. Its
relationship to ![]() -distances is described in
[6]. This earlier algorithm has been
successfully used in commercial applications, especially for spelling
correction in word processing software, typewriters, and hand-held
dictionary devices (we estimate that that over 15,000,000 such
software/hardware units have been sold by Proximity Technology,
Franklin Electronic Publishers and their licensees). Other less
prominent commercial applications include database field search (e.g.,
looking up a name or address), and the analysis of multi-field records
such as mailing addresses, in order to eliminate near-duplicates. In
both of these applications, the strict global left-right ordering
imposed by
-distances is described in
[6]. This earlier algorithm has been
successfully used in commercial applications, especially for spelling
correction in word processing software, typewriters, and hand-held
dictionary devices (we estimate that that over 15,000,000 such
software/hardware units have been sold by Proximity Technology,
Franklin Electronic Publishers and their licensees). Other less
prominent commercial applications include database field search (e.g.,
looking up a name or address), and the analysis of multi-field records
such as mailing addresses, in order to eliminate near-duplicates. In
both of these applications, the strict global left-right ordering
imposed by ![]() time `edit distance' methods, can be problematic.
On the other hand, very local left-right order preservation seems to
be an important part of similarity perception in humans. One simple
adaptation of our
time `edit distance' methods, can be problematic.
On the other hand, very local left-right order preservation seems to
be an important part of similarity perception in humans. One simple
adaptation of our ![]() -distance methods which goes a long way
towards capturing this characteristic, consists of extending the
alphabet beyond single symbols to include digraphs or multi-graphs.
The result is increased sensitivity to local permutation. Another
effective alphabet extension technique involves the addition of feature symbols to the alphabet to mark events such as likely
phonetic transitions. We expect that the use of general concave-down
distance functions (as opposed to
-distance methods which goes a long way
towards capturing this characteristic, consists of extending the
alphabet beyond single symbols to include digraphs or multi-graphs.
The result is increased sensitivity to local permutation. Another
effective alphabet extension technique involves the addition of feature symbols to the alphabet to mark events such as likely
phonetic transitions. We expect that the use of general concave-down
distance functions (as opposed to ![]() ) will improve the quality
of the similarity judgments possible within the
) will improve the quality
of the similarity judgments possible within the ![]() -distance
framework.
-distance
framework.
The development above considers strings of equal length only. The
unequal length case is not a difficult generalization; but considering
it does highlight the issue of embedding. By this we mean that
it is implicit in our formulation that the two strings are in a sense
embedded into the real line. The particular rather natural embedding
we've assumed so far, maps ![]() and
and ![]() to value
to value ![]() on the real
line - but others are possible.
on the real
line - but others are possible.
A detailed comparison of our methods with `edit distance' approaches
is beyond the scope of this paper. But we must point out that the
`edit distance' formulation is in several senses richer than
ours. First, the cost of matching different alphabet members need not
be fixed. Also, our distance formulation depends on a designated
embedding while the `edit distance' method requires no such
specification. Finally, for some problems, left-right order
preservation may be desirable. On the other hand, even the simplest
`edit distance' approach is ![]() ; compared with the
; compared with the ![]() or
or ![]() complexity of our method. We therefore feel that additional work is
needed to better understand the applications of our approach -- and perhaps extend
it.
complexity of our method. We therefore feel that additional work is
needed to better understand the applications of our approach -- and perhaps extend
it.
We wish to thank Dina Kravets, Dave Robinson, and Warren Smith for helpful discussions -- and Dave Robinson and Kirk Kanzelberger for implementing and testing the algorithms described above.
(in preparation).
This document was generated using the LaTeX2HTML translator Version 2K.1beta (1.47)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -image_type gif -nonext_page_in_navigation -noprevious_page_in_navigation -up_url ../main.html -up_title 'Publication homepage' -numbered_footnotes quasi.tex
The translation was initiated by Peter N. Yianilos on 2002-07-06