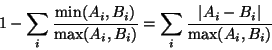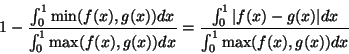Up: Publication homepage
Normalized Forms for Two Common Metrics
Peter N. Yianilos1
12/5/91 Rev 2/27/92 Rev 7/7/2002
Abstract:
We show that symmetric set difference and Euclidian distance
have particular
![$[0-1]$](img3.gif) normalized
normalized forms that remain
metrics.
The first of these
 is easily
established and generalizes to measure spaces.
is easily
established and generalizes to measure spaces.
The second applies to vectors in
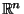 and is given by
and is given by
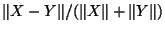 . That this is a metric is more
difficult to demonstrate and is true for Euclidian distance
(the
. That this is a metric is more
difficult to demonstrate and is true for Euclidian distance
(the 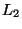 norm) but for no other integral Minkowski metric.
The short and elegant proof we give is due to David Robbins and
Marshall Buck [1].
norm) but for no other integral Minkowski metric.
The short and elegant proof we give is due to David Robbins and
Marshall Buck [1].
We also explore a number of variations.
Keywords: Metric Space,
Distance Function,
Similarity Function/Coefficient,
Euclidian Distance,
Association,
Clustering,
Vector Quantization,
Pattern Recognition,
Statistical Methods.
The notion of Metric Space [2], is a
cornerstone of mathematical topology and analysis, and is
often employed in pattern recognition and clustering systems.
The third item in this definition is usually referred to as
the triangle inequality. It is worthwhile noting that
not all approaches to pattern recognition and clustering
impose this requirement. The term similarity measure
or dissimilarity measure, or some variation thereof, is
then used to describe the comparison function.
Two well known examples of metric spaces are Euclidian  -space
with:
-space
with:
and the symmetric difference metric on members of  , the
set consisting of all finite sets:
, the
set consisting of all finite sets:
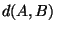 is of course geometrical length, and
is of course geometrical length, and
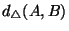 simply counts the number of elements on
which
simply counts the number of elements on
which 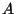 and
and 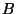 disagree.
disagree.
Both of these metrics are in general unbounded, and their
value is independent of the size of 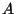 and
and 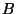 . I.e.
two very large sets that have three points of disagreement,
are just as distant under
. I.e.
two very large sets that have three points of disagreement,
are just as distant under 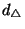 as two very small sets
which also differ by three elements. In Euclidian
as two very small sets
which also differ by three elements. In Euclidian 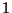 -space,
values
-space,
values 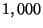 and
and 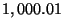 are just as distant as
are just as distant as
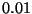 and
and 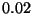 .
.
Hence we may in a sense view 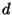 and
and 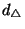 as measures
of absolute distance or difference.
as measures
of absolute distance or difference. 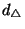 is
seen to be insensitive to
is
seen to be insensitive to 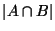 while
while 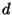 does not
independently consider
does not
independently consider 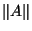 and
and 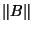 when measuring
distance.
when measuring
distance.
It is therefore natural to consider forming relative
distance measures for these underlying spaces, since such
measures may be more effective in the solution of certain
problems. Certainly the notion of relative error is an
important one in numerical analysis. For sets, and Euclidian
space, size might naturally be taken to mean cardinality,
and norm respectively. Thus we are interested in set metrics
which measure relative to the empty set, and in an
alternative to the Euclidian distance metric which measures
relative to the origin.
With no domain assumptions, 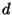 and
and 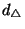 are
unbounded. This may create algorithmic difficulty (or at a
minimum inconvenience). Thus converting these metrics to
bounded forms may sometimes be useful.
are
unbounded. This may create algorithmic difficulty (or at a
minimum inconvenience). Thus converting these metrics to
bounded forms may sometimes be useful.
The simplest way in general to effect a bound is to compose
the metric with another function 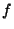 which acts as a range
compander such that the combination still satisfies
definition 1. One well known example
of such a function that bounds any metric to
which acts as a range
compander such that the combination still satisfies
definition 1. One well known example
of such a function that bounds any metric to ![$[0,1]$](img34.gif) is:
is:
There are many such formulas for bounding metrics. It may
for example be shown that the sum of metrics is a metric, and
beyond this that a metric results from composition with any
continuous, differentiable, strictly increasing function 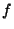 such that
such that 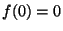 , and
, and 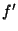 is non-increasing.
2
is non-increasing.
2
Since however any such method depends only on the value
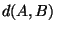 , the bounded form will inherit the absolute or
relative behavior of its unbounded parent.
, the bounded form will inherit the absolute or
relative behavior of its unbounded parent.
These metric companding methods are in contrast to
normalization to which we now turn.
In the sections that follow we will introduce the metric
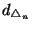 defined by
defined by
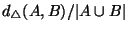 and also
metric
and also
metric 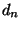 defined
3 by
defined
3 by
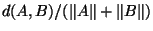 .
.
In contrast to the absolute behavior of 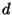 and
and
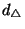 these functions judge distance with consideration
to the relative location of the origin and empty set
respectively.
these functions judge distance with consideration
to the relative location of the origin and empty set
respectively.
That they are in fact metrics is not obvious and a
considerable portion of this paper is devoted to the required
proofs.
We will also present a number of alternative forms including
mixed metrics that combine absolute and relative behavior.
To normalize the symmetric difference metric we choose to
divide its value by the size of the union of its arguments.
More formally we have:
Definition 2
Let
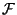
be the set consisting of all finite sets
We define function
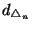
on
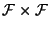
by:
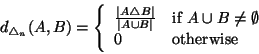 |
(1) |
We would point out here that not every reasonable attempt at
normalization results in a metric. Dividing instead by
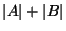 , an altogether sensible thing to do, fails to
satisfy the triangle inequality. This may be seen by letting
, an altogether sensible thing to do, fails to
satisfy the triangle inequality. This may be seen by letting
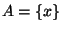 ,
, 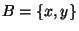 , and
, and 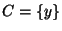 . The
. The 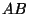 and
and 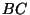 distances
are then both
distances
are then both 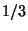 while the distance
while the distance 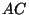 is
is 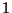 .
4
.
4
While it is clear that this function is bounded by ![$[0,1]$](img34.gif) ,
and that its behavior is more relative in that
,
and that its behavior is more relative in that 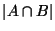 will affect its value, it must be demonstrated that
will affect its value, it must be demonstrated that
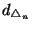 is in fact a metric.
is in fact a metric.
Proof: We must show that for all finite sets 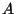 ,
,
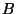 , and
, and 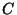 , the following are true:
, the following are true:
We have i) because
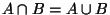 only when
only when
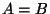 . The second requirement ii) is clear from the
commutivity of basic set operations.
. The second requirement ii) is clear from the
commutivity of basic set operations.
Item iii), the triangle inequality, requires more
work. Using EQ 1, we must show:
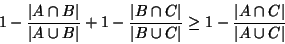 |
(2) |
It is easy to verify that this is true if
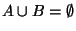 ,
,
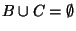 , or
, or
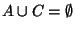 , So we restrict our attention to the case in which
none of the denominators in EQ 2 is zero.
, So we restrict our attention to the case in which
none of the denominators in EQ 2 is zero.
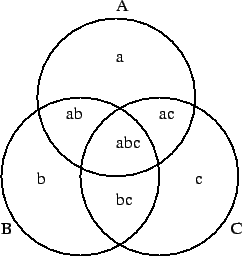
Now the union of sets A,B, and C, may be partitioned (see
figure 1) into seven disjoint subsets whose
orders we denote:
Figure 1:
Partitioning
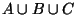
|
For later convenience we also define
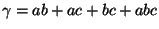 .
.
With these definitions, EQ 2 becomes with some
simplification:
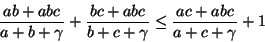 |
(3) |
Now observe that 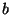 may be removed without loss of
generality from the left denominator, since its removal
can only increase that side. It will then suffice to show that:
may be removed without loss of
generality from the left denominator, since its removal
can only increase that side. It will then suffice to show that:
Now replacing 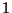 with
with
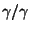 and adding fractions,
we arrive at:
and adding fractions,
we arrive at:
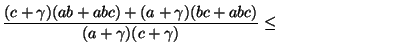 |
| |
|
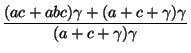 |
(5) |
The denominator of EQ 4 is equal to the
denominator in EQ 5 plus 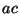 , and is
therefore no smaller.
, and is
therefore no smaller.
It therefore suffices to show the that the inequality is true
for the numerators alone, i.e. that:
Starting from the left side of this inequality we have:
and we are done. 
Our arguments for sets in 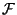 generalize easily to
measure spaces[3,4]. The case
of finite non-zero measures is straightforward since these
correspond well with finite sets and our earlier arguments.
generalize easily to
measure spaces[3,4]. The case
of finite non-zero measures is straightforward since these
correspond well with finite sets and our earlier arguments.
To see this, remember that for any
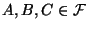 , we
earlier expressed the triangle inequality in terms of the
orders of their natural decomposition into seven disjoint
parts. Our proof of theorem 1 may then be
viewed as establishing the truth of an inequality in these
seven independent variables - an inequality that holds for
any assignment of finite non-negative values; subject only to
the restriction that the denominators may not vanish. The
same decomposition applies if
, we
earlier expressed the triangle inequality in terms of the
orders of their natural decomposition into seven disjoint
parts. Our proof of theorem 1 may then be
viewed as establishing the truth of an inequality in these
seven independent variables - an inequality that holds for
any assignment of finite non-negative values; subject only to
the restriction that the denominators may not vanish. The
same decomposition applies if
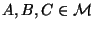 , with the
inequality relating measure instead of set order, thus
motivating the connection between
, with the
inequality relating measure instead of set order, thus
motivating the connection between
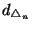 and measure spaces.
and measure spaces.
As a practical matter the finite setting is the most
important case. However the generalization extends fully to
measures which assume value 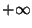 , and we will take the
time to show this.
, and we will take the
time to show this.
For elements of finite non-zero measure, definition of our
metric will correspond to simple generalization of the notion
of set order, to that of measure. For elements in general,
several cases are necessary to patch together a definition.
While these special cases manage to define the metric for all
members of the space, only the simplest discrete distance
notion applies to elements with zero or infinite measure.
Definition 3
Let
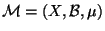
, be a measure
space, and
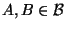
. We define function
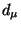
on
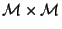
by:
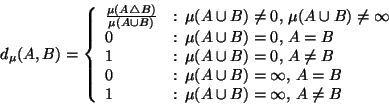 |
(6) |
We now state the corollary:
Proof:
Everything but the triangle inequality follows immediately from
the definition.
Note first that if 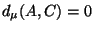 or either one of
or either one of
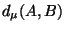 ,
, 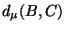 is one, then the triangle
inequality is trivially established. So in particular the
inequality is satisfied if
is one, then the triangle
inequality is trivially established. So in particular the
inequality is satisfied if 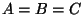 .
.
Further observe that if 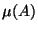 or
or 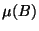 is infinite or
zero, then
is infinite or
zero, then 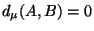 iff
iff 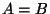 , and one otherwise. I.e.
the definition reduces to a simple equality test for these
cases.
, and one otherwise. I.e.
the definition reduces to a simple equality test for these
cases.
With these points in mind we distinguish three cases:
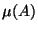 ,
, 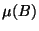 ,
, 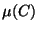 are finite with no two zero:
Interpreting set order
are finite with no two zero:
Interpreting set order 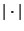 instead as
measure
instead as
measure 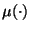 , the denominators of
EQ 2 are all non-zero and our
proof of theorem 1 applies.
, the denominators of
EQ 2 are all non-zero and our
proof of theorem 1 applies.
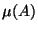 ,
, 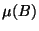 ,
, 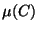 are finite and at least two
are zero:
If
are finite and at least two
are zero:
If
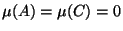 and
and 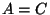 , then
, then
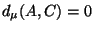 . On the other hand
. On the other hand 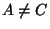 implies
implies 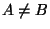 or
or 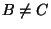 so that either
so that either
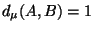 or
or 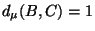 .
.
Otherwise we may assume without loss of generality that
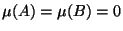 . Here
. Here 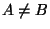 implies
implies
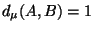 - and if
- and if 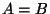 , then
, then
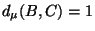 unless
unless 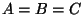 .
.
- At least one of
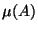 ,
, 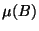 ,
, 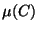 is infinite:
If
is infinite:
If 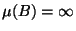 then
then 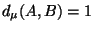 or
or
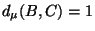 , unless
, unless 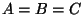 .
.
Otherwise we may assume without loss of generality that
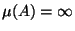 . But then
. But then 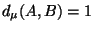 unless
unless 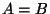 , in which case
, in which case 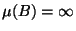 ; a
situation covered by the preceding argument.
; a
situation covered by the preceding argument.

Proceeding further we can develop a slightly more general
form for 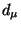 . Consider some
. Consider some
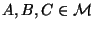 and
their associated decomposition. Now for some
and
their associated decomposition. Now for some 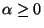 ,
adding
,
adding 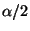 to each of
to each of 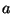 ,
, 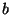 , and
, and 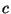 , leaves them
non-negative and the inequality therefore valid.
, leaves them
non-negative and the inequality therefore valid.
This may be thought of as extending each of 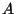 ,
, 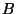 , and
, and 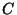 ,
by a new region which does not intersect the others.
,
by a new region which does not intersect the others.
Equation 3 then becomes:
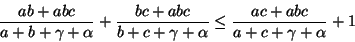 |
(7) |
This all motivates:
Definition 4
Let
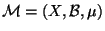
be a measure space,
and
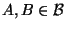
. We define function
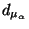
on
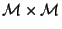
by:
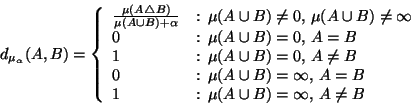 |
(8) |
for 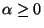 .
.
And from our discussion above it follows that:
Corollary 2
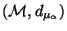
is a metric space.
Thus we see that the 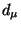 discontinuity when
discontinuity when 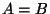 may be
eliminated
5 by biasing the denominator term
may be
eliminated
5 by biasing the denominator term 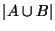 . Function
. Function
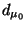 is just
is just 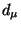 , and as
, and as
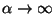 , the behavior of
, the behavior of
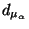 approaches that of
simple symmetric difference.
approaches that of
simple symmetric difference.
In a later section we will present several examples of metrics
that arise from the results above. Before doing so however,
we turn our attention back to Euclidian space and our goal of
establishing a normalized metric there.
In this section we will demonstrate that Euclidian distance
normalized by combined norm, defines an alternative and ![$[0,1]$](img34.gif) bounded metric on
bounded metric on
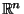 .
.
Definition 5
Let
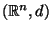
denote Euclidian N-space (The
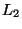
norm and corresponding standard distance function).
Then the following [0,1] bounded function
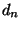
of
any two vectors
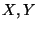
is defined to be the
Normalized Euclidian Distance between
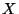
and
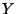
:
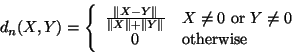 |
(9) |
That this definition is in fact a metric will later be stated
as a theorem. Its proof will require a series of Lemmas
which build insight into the function.
It is worthwhile noting that in
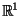 , an easy proof exists
and that a very similar
, an easy proof exists
and that a very similar
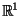 metric (a special case of our
definition 6), is employed in
[5].
metric (a special case of our
definition 6), is employed in
[5].
We would also observe that this definition fails to generate a
metric if the 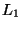 norm is substituted. 6 For if
norm is substituted. 6 For if
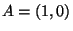 ,
, 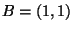 , and
, and 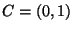 , the triangle inequality
does not hold. The
, the triangle inequality
does not hold. The  norm also fails; consider
norm also fails; consider
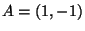 ,
, 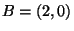 , and
, and 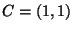 . For this example, and
the
. For this example, and
the 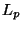 norm, the triangle inequality becomes:
norm, the triangle inequality becomes:
This fails for 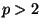 . Therefore, we have that our
definition does not generate a metric for any of the
integral Minkowski metrics
. Therefore, we have that our
definition does not generate a metric for any of the
integral Minkowski metrics 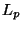 where
where 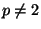 .
.
Our to-be-proven positive result for 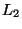 is thus that much
more interesting.
is thus that much
more interesting.
Proof:
Let 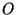 ,
, 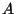 ,
, 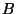 ,
, 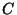 be four distinct points in Euclidean space.
Then
be four distinct points in Euclidean space.
Then
proof: Let 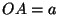 ,
, 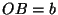 ,
, 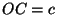 ,
, 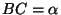 ,
, 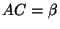 ,
, 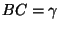 .
Then we need to prove that
.
Then we need to prove that
Note that we have
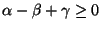 by the triangle inequality
and
by the triangle inequality
and
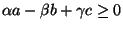 by Ptolemy's inequality.
We may suppose that
by Ptolemy's inequality.
We may suppose that 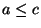 .
.
Case 1: 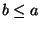 . Then we have
. Then we have
and the theorem follows immediately.
Case 2:
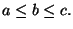 Then we have
Then we have
from which the result follows immediately as well.
Case 3: 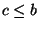 . Observe that the theorem is true for four points
. Observe that the theorem is true for four points
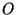 ,
, 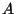 ,
, 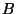 ,
, 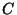 if and only if it is true for
if and only if it is true for 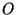 and the points
and the points
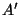 ,
, 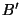 ,
, 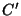 obtained by inverting
obtained by inverting 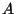 ,
, 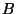 and
and 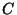 in the sphere
of radius 1 centered at
in the sphere
of radius 1 centered at 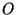 . (Recall that
. (Recall that 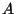 and
and 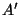 are on the
same ray from
are on the
same ray from 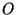 and satisfy
and satisfy 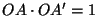 . The key fact that is
needed is
. The key fact that is
needed is
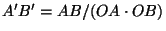 .) This reduces
case 3 to case 1.
.) This reduces
case 3 to case 1.

If we now label the origin as  , we may re-state the theorem
as a corollary in purely geometrical terms:
, we may re-state the theorem
as a corollary in purely geometrical terms:
Corollary 3
Let
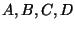
be four points in Euclidian Space and
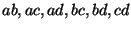
, denote their interpoint segment lengths.
Then:
So despite a singularity at the
origin, 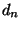 imposes a metric on
imposes a metric on
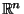 . This amounts to
a fully relative distance measure which clearly cannot
well cope with zero. By contrast, standard Euclidian
distance may be viewed as a fully absolute distance
measure. It is easy to imagine a continuum of intermediate
metrics which are partially relative.
. This amounts to
a fully relative distance measure which clearly cannot
well cope with zero. By contrast, standard Euclidian
distance may be viewed as a fully absolute distance
measure. It is easy to imagine a continuum of intermediate
metrics which are partially relative.
Furthermore, some applications, while requiring a modicum of
relative behavior, may also require better behavior at
the origin than 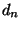 provides.
provides.
All of this motivates the following definition:
Definition 6
Let
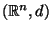
denote Euclidian N-space. Then for
values
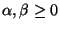
, with
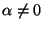
or
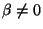
, the following
![$[0,1/\beta]$](img163.gif)
bounded function
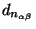
of any two vectors
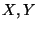
is defined to be the
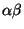 -Normalized Euclidian Distance
-Normalized Euclidian Distance
between
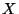
and
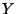
:
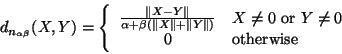 |
(12) |
The Normalized Euclidian Distance of
definition 9 corresponds to
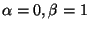 . Note that the definition 6's
special condition at
. Note that the definition 6's
special condition at 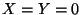 is only required when
is only required when 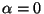 ,
for when
,
for when 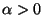 , the denominator cannot vanish.
, the denominator cannot vanish.
The case 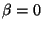 , merely corresponds to standard Euclidian
distance scaled by
, merely corresponds to standard Euclidian
distance scaled by 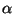 .
.
In between these two extremes lies a family of hybrid
functions that combine the relative behavior of 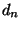 with the
absolute behavior of
with the
absolute behavior of 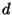 .
.
To establish that
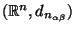 is in general a metric
space, we will require one lemma concerning the behavior of
quasi-quadrilaterals in
is in general a metric
space, we will require one lemma concerning the behavior of
quasi-quadrilaterals in
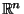 .
.
Lemma 1
Let
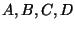
be any four points in
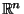
, then
with respect to the six interpoint segment lengths:
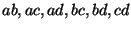
, the following is true:
I.e. the sum of the product of the lengths of
opposite sides of an arbitrary quadrilateral, is no
smaller than the product of its diagonals.
Proof: We have only to argue that we may reduce
setting to
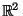 since there, the lemma is recognized as a
standard theorem of inversive geometry ([6]
Theorem 5.12) - a direct generalization of Ptolemy's theorem.
since there, the lemma is recognized as a
standard theorem of inversive geometry ([6]
Theorem 5.12) - a direct generalization of Ptolemy's theorem.
Since any four points may be embedded in
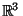 , we may
assume our setting is at most this.
, we may
assume our setting is at most this.
Within
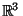 , choose coordinates so that
, choose coordinates so that 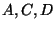 lie on
the
lie on
the 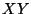 plane, and
plane, and 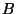 is located above (or on) it. I.e.
is located above (or on) it. I.e.
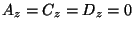 and
and 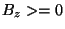 .
.
Now translate so that  is the origin.
is the origin.
Further choose rotation and orientation so that line  is
parallel to and above the X-axis with
is
parallel to and above the X-axis with 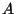 left of
left of 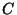 . I.e.
. I.e.
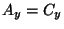 and
and 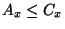 .
.
Now consider spheres 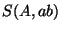 and
and 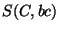 . The
intersection of these spheres is a circle perpendicular to
the XY plane and parallel to the Y-axis, having center along
. The
intersection of these spheres is a circle perpendicular to
the XY plane and parallel to the Y-axis, having center along
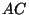 .
.
Any choice for 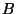 along on this circle it will leave
everything unchanged in our inequality but for
along on this circle it will leave
everything unchanged in our inequality but for 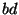 .
.
Notice that the point on this circle farthest from the
origin, is just its intersection with the XY plane.
Denoting this point 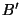 and relocating
and relocating 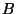 there, increases
there, increases
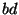 and and the inequality's right side, while leaving the
left unchanged.
and and the inequality's right side, while leaving the
left unchanged.
Thus it is clear that the inequality is true for points
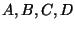 in
in
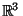 iff it is true for
iff it is true for 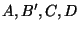 in
in
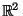 .
. 
We are now ready to establish that
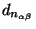 is a metric:
is a metric:
Corollary 4
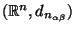
is a metric space.
Proof: The first and second metric conditions
are straightforward. We therefore turn to the triangle
inequality.
If 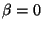 , then by definition
, then by definition 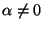 and
and
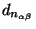 is
nothing more than scaled Euclidian distance. If
is
nothing more than scaled Euclidian distance. If 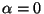 ,
then by definition
,
then by definition 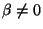 and
and
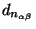 is just scaled
normalized Euclidian distance.
is just scaled
normalized Euclidian distance.
So the only interesting case is that in which
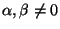 . Here, we may assume without loss of generality that
. Here, we may assume without loss of generality that 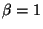 since other
cases may be reduced to this one by multiplying each term in the
triangle inequality by
since other
cases may be reduced to this one by multiplying each term in the
triangle inequality by 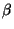 and then reducing.
and then reducing.
Now defining for convenience:
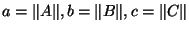 , it
remains for us to show that:
, it
remains for us to show that:
Now forming a common denominator, discarding it, and then
rearranging, we have:
We now separately consider matched lines from either side of
this expression. It turns out that the inequality holds for
each such pairing, thus establishing the overall inequality.
The inequality for the first line is just scaled ordinary
Euclidian distance. Then, letting 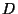 denote the origin, the
inequality holds for the second line due to
corollary 3, and for the third
7 due to
lemma 1.
denote the origin, the
inequality holds for the second line due to
corollary 3, and for the third
7 due to
lemma 1. 
To illustrate the wide variety of metrics that can be
constructed with our earlier results, we start by returning to
metrics on 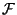 .
.
We first observe that finite sets may be regarded as binary
vectors in Euclidian space. With this observation
theorem 2 gives us that the following
is a metric:
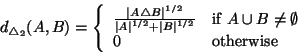 |
(13) |
It is interesting to note that without the square root
operations, this definition corresponds to normalization of
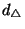 by
by 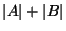 , which was earlier shown not to be
a metric.
, which was earlier shown not to be
a metric.
Again thinking of sets as binary vectors or variables, metric
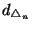 is recognized as a well known measure of association
referred to as the Jaccard coefficient
[7], or S-coefficient:
is recognized as a well known measure of association
referred to as the Jaccard coefficient
[7], or S-coefficient:
Where 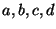 refer to the standard entries in a 2-by-2
contingency (or association) table for binary variables.
This very basic comparison function may be expressed in many
forms. Expressing essentially the same thing as a similarity
measure corresponds to the Tanimoto Coefficient,
[8], operating on binary vectors:
refer to the standard entries in a 2-by-2
contingency (or association) table for binary variables.
This very basic comparison function may be expressed in many
forms. Expressing essentially the same thing as a similarity
measure corresponds to the Tanimoto Coefficient,
[8], operating on binary vectors:
In the language of computer programming this is just the
count of 1's in the exclusive or of bit vectors 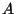 and
and
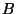 , divided by the count of 1's in their logical or.
, divided by the count of 1's in their logical or.
In [9], the measure is referred to as association. While the authors do not state that these
various forms fail to satisfy the triangle inequality, they
describe them along with other non-metric measures.
Other sources such as [10] mention
explicitly the set function
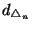 , but again fail to note
that it satisfies the triangle inequality.
, but again fail to note
that it satisfies the triangle inequality.
The Bray-Curtis measure[11], is written:
and is recognized as our 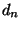 but under the
but under the 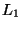 norm. Now
we have seen that this does not form a metric, but since
norm. Now
we have seen that this does not form a metric, but since
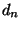 is a metric we may write:
is a metric we may write:
with the knowledge that this does form a metric.
Also in [11], the reader will recognize the
Canberra Metric as 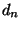 in
in
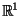 , making
, making 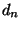 a
considerable generalization of this apparently well known
metric.
a
considerable generalization of this apparently well known
metric.
In familiar settings such as
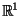 and
and
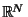 , with measure
, with measure 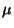 defined as
length/ area/ volume, the metric
defined as
length/ area/ volume, the metric 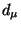 corresponds to the
amount of non-common length/ area/ volume, normalized by the
total length/ area/ volume.
corresponds to the
amount of non-common length/ area/ volume, normalized by the
total length/ area/ volume.
Here are some examples of metrics derived from
corollary 1, that are defined for
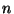 -tuples of non-negative values. For brevity's sake, we
will not show the
-tuples of non-negative values. For brevity's sake, we
will not show the 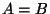 case for which any metric must evaluate
to zero.
case for which any metric must evaluate
to zero.
- Thinking of our
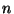 -tuple as a histogram in the plane,
we may write:
-tuple as a histogram in the plane,
we may write:
This may be viewed as a repaired Bray-Curtis
measure in that
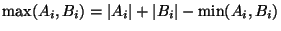 . I.e. the denominator has an
extra term which suffices to form a metric.
. I.e. the denominator has an
extra term which suffices to form a metric.
- We may take the direct product of metric spaces, and
combine metrics by any linear combination with the
result still a metric. Thus we have in particular that:
which resembles somewhat our first example but behaves
quite differently.
- Imagining now that our vectors represent the
dimensions of an N-dimensional solid object rooted at
the origin, and defining measure as volume, we have:
An example in which a single component greatly
influences the resulting value.
Now corollary 1 may also be applied to
function spaces. Let ![$C[0,1]$](img206.gif) denote the space of
non-negative continuous functions on
denote the space of
non-negative continuous functions on ![$[0,1]$](img34.gif) . Given
. Given
![$f,g \in
C[0,1]$](img207.gif) , the metric defined by:
, the metric defined by:
may be thought of as an extension of our first positive
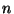 -tuple metric above, as
-tuple metric above, as
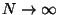 , or in a
Lebesgue/Measure-Space context.
, or in a
Lebesgue/Measure-Space context.
Extending our second 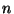 -tuple metric to Riemann integrable
functions allows us to write:
-tuple metric to Riemann integrable
functions allows us to write:
Note that in some cases, and with the proper assumptions,
the continuity and range of integration assumptions made above
may be relaxed.
Now for the sake of brevity, we have focused mainly on
examples using
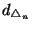 /
/ 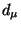 . Similar constructions apply
to
. Similar constructions apply
to 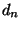 for both
for both 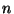 -tuples and function spaces.
-tuples and function spaces.
It is worthwhile noting (however obvious) that 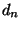 may also
be viewed as an alternate metric for the complex plane with
may also
be viewed as an alternate metric for the complex plane with
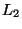 norm corresponding to complex absolute value.
norm corresponding to complex absolute value.
We close this section by commenting that 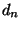 used as a
measure of relative error in numerical analysis, may prove
interesting. Given a sequence
used as a
measure of relative error in numerical analysis, may prove
interesting. Given a sequence
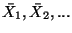 of
approximate solutions, we might define
of
approximate solutions, we might define
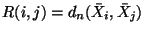 and the triangle inequality would
then give us that:
and the triangle inequality would
then give us that:
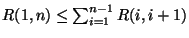 .
.
We have developed normalized forms for two important metrics
and shown each to be an endpoint of a continuum of metric
functions ranging to the original unnormalized forms.
In a combinatorial setting,
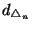 may be viewed as a
prototype for constructing a normalized bounded metric for
many applications - for every injection of a pattern space
into
may be viewed as a
prototype for constructing a normalized bounded metric for
many applications - for every injection of a pattern space
into  induces a metric on the original pattern
space.
8
induces a metric on the original pattern
space.
8
Furthermore, evaluating this metric is possible given only
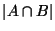 and the individual orders
and the individual orders 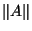 , and
, and 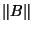 since
since
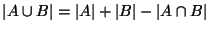 .
.
In practice, these values may sometimes be directly computed
without explicitly forming injective images in set space.
In [12] a VLSI chip is described which in
computes these three orders for a particular mapping of
finite symbol strings into  , and combines them to
define a measure of string similarity.
, and combines them to
define a measure of string similarity.
In more Euclidian settings, the family
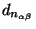 may be used
where normalized behavior is required and the metric triangle
inequality is of value, e.g. in finding nearest neighbors, or
when bounding sequential sums of distances.
may be used
where normalized behavior is required and the metric triangle
inequality is of value, e.g. in finding nearest neighbors, or
when bounding sequential sums of distances.
Beyond the existence and basic properties established in this
paper, one may examine a number of topics including the
notion of colinearity in these normalized spaces, the nature
of the geodesics corresponding to 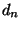 , and questions of
statistical behavior.
, and questions of
statistical behavior.
I thank David Robbins and Marshall Buck for their proof that
replaces the tortuous argument I first discovered and gave in
an earlier version of this paper.
I also thank
C.W. Gear,
N. Littlestone,
I. Rivin, and
W.D. Smith,
for helpful discussions and references, E. Baum, for corrections and
general assistance,
- and S.R. Buss for his
interest in and help with my work over many years.
- 1
-
D. Robbins and M. Buck. Private Communication, May 1993.
- 2
-
J. L. Kelly, General Topology.
New York: D. Van Nostrand, 1955.
- 3
-
H. L. Royden, Real Analysis.
New York: Macmillan Publishing, second ed., 1968.
- 4
-
R. G. Bartle, The Elements of Integration.
John Wiley & Sons, Inc., 1966.
- 5
-
D. Haussler, ``Decision theoretic generalizations of the pac model for neural
net and other learning applications,'' Tech. Rep. UCSC-CRL-91-02, University
of California, Santa Cruz, December 1990.
- 6
-
H. Coxeter and S. Greitzer, Geometry Revisited.
Washington, D.C.: Mathematical Association of America, 1967.
- 7
-
L. Kaufman and P. J. Rousseeuw, Finding groups in data: an introduction to
cluster analysis.
John Wiley & Sons, Inc., 1990.
- 8
-
R. O. Duda and P. E. Hart, Pattern Classification and Scene Analysis.
John Wiley & Sons, Inc., 1973.
- 9
-
A. Kandel, Fuzzy techniques in pattern recognition.
John Wiley & Sons, Inc., 1982.
- 10
-
R. J. Schalkoff, Pattern recognition: statistical, structural, and neural
approaches.
John Wiley & Sons, Inc., 1992.
- 11
-
A. Ralston, Statistical Methods for Digital Computers.
John Wiley & Sons, Inc., 1977.
- 12
-
P. N. Yianilos, ``A dedicated comparator matches symbol strings fast and
intelligently,'' Electronics Magazine, December 1983.
Normalized Forms for Two Common Metrics
This document was generated using the
LaTeX2HTML translator Version 2K.1beta (1.47)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -image_type gif -nonext_page_in_navigation -noprevious_page_in_navigation -up_url ../main.html -up_title 'Publication homepage' -numbered_footnotes nmet.tex
The translation was initiated by Peter N. Yianilos on 2002-07-07
Footnotes
- ... Yianilos1
-
This is a revision of an earlier unpublished Technical Memorandum
of NEC Research
Institute, 4 Independence Way, Princeton, NJ 08540
- ... non-increasing.2
-
The key is that
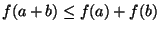 .
.
- ... defined3
-
Both of these metrics are defined to have zero
value if
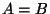 .
.
- ....
4
- This example noticed by S.R. Buss who also pointed
out that this definition satisfies a weakened triangle inequality.
- ... eliminated5
-
The same applies for
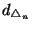 .
.
- ... substituted.6
- This may
also be seen as a result of our earlier comments regarding
other methods for normalizing
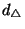 .
.
- ... third7
-
Factor
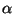 may be disregarded as it applies to
all terms, and re-grouping the paired sums, yields
a common term
may be disregarded as it applies to
all terms, and re-grouping the paired sums, yields
a common term 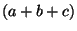 which may be similarly disregarded.
which may be similarly disregarded.
- ... space.8
-
For measure spaces we must additionally require that
if
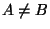 , then their images differ by more than
a set of measure zero.
, then their images differ by more than
a set of measure zero.
Up: Publication homepage
Peter N. Yianilos
2002-07-07
![]() is easily
established and generalizes to measure spaces.
is easily
established and generalizes to measure spaces.
![]() and is given by
and is given by
![]() . That this is a metric is more
difficult to demonstrate and is true for Euclidian distance
(the
. That this is a metric is more
difficult to demonstrate and is true for Euclidian distance
(the ![]() norm) but for no other integral Minkowski metric.
The short and elegant proof we give is due to David Robbins and
Marshall Buck [1].
norm) but for no other integral Minkowski metric.
The short and elegant proof we give is due to David Robbins and
Marshall Buck [1].
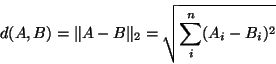
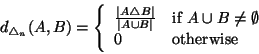
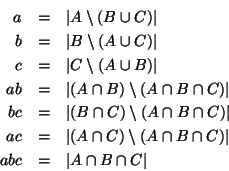
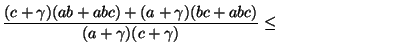
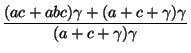
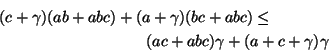
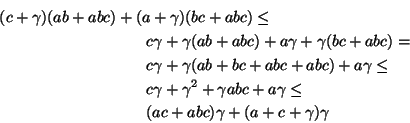
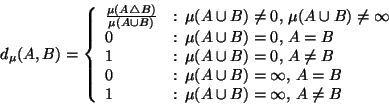
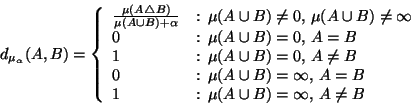
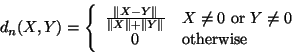
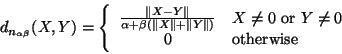
![\begin{eqnarray*}
\left.
\begin{array}{l}
\alpha^2 d(A,B) + \alpha^2 d(B,C) +...
...ptstyle (a+b)}+{\scriptstyle (b+c)}d(A,C)]
\end{array} \right.
\end{eqnarray*}](img192.gif)
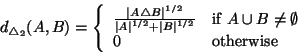
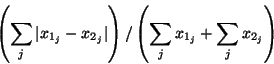
![\begin{displaymath}
\left(
\sum_j \vert x_{1_j} - x_{2_j} \vert^2
\right)^{1/...
...ight]^{1/2} +
\left[ \sum_j x_{2_j}^2 \right]^{1/2}
\right)
\end{displaymath}](img199.gif)