Metric Learning via Normal Mixtures

Peter N. Yianilos ¹

October 4, 1995

Abstract:

Natural learners rarely have access to perfectly labeled data - motivating the study of unsupervised learning in an attempt to assign labels. An alternative viewpoint, which avoids the issue of labels entirely, has as the learner's goal the discovery of an effective metric with which similarity judgments can be made. We refer to this paradigm as metric learning. Effective classification, for example, then becomes a consequence rather than the direct purpose of learning.

Consider the following setting: a database made up of exactly one observation of each of many different objects. This paper shows that, under admittedly strong assumptions, there exists a natural prescription for metric learning in this data starved case.

Our outlook is stochastic, and the metric we learn is represented by a joint probability density estimated from the observed data. We derive a closed-form expression for the value of this density starting from an explanation of the data as a Gaussian Mixture. Our framework places two known classification techniques of statistical pattern recognition at opposite ends of a spectrum - and describes new intermediate possibilities. The notion of a stochastic equivalence predicate is introduced and striking differences between its behavior and that of conventional metrics are illuminated. As a result one of the basic tenets of nearest-neighbor-based classification is challenged.

Keywords -- Nearest Neighbor Search, Metric Learning, Normal/Gaussian Mixture Densities, Unsupervised Learning, Neural Network, Encoder Network.

Introduction

We consider the problem of metric learning. That is, given a sample from some observation space, infer something about what distance should mean. The observations we consider are represented by vectors from a finite dimensional real vector space. To put this work in perspective we begin by reviewing two common approaches to pattern classification.

In the statistical pattern recognition outlook[1], one typically assumes that patterns are generated by some process of change operating on one or more starting points. Commonly these starting points represent vector means of object classes, and the process of change is assumed to be modeled by normal densities about these means. If many members of each class are available for training, then one may estimate a mean vector and covariance matrix for each class. Combined with some prior distribution on the classes themselves, it is then straightforward to compute the a posteriori probability of an unknown vector, given the model. But when few members of each class are available (perhaps only one), this approach breaks down.

In the nearest neighbor outlook, one does not need a label for each point to identify nearest neighbors. But the label is used to guess the query's label based on the neighbor's labels. In the limit (vast amounts of data) it may be argued that the metric is not important - but in almost all practical problem domains it certainly is. Humans for example can classify numeric digits long before they've seen enough examples so that pixel by pixel correlation yields a satisfactory result. Improved metrics for nearest neighbor classification were proposed by Fukanaga et al in [2] and [3], and later in [4] and [5]. But again, given very few members of each class, or in the entirely unsupervised case, their results do not apply and it is not at all clear what if anything can be done to choose a good metric.

We propose an approach for these data-starved cases drawn from the stochastic modeling outlook. The general message of this paper is that, given assumptions, one can sometimes infer a metric from a stochastic model of the training data. We focus on mixtures of normal densities, but suggest that analogous inferences might be made from a broader class of models.

We've used the term metric above in its most general sense, but nearest neighbor classification systems do not always employ distance functions that are metrics in the accepted mathematical sense. Moreover, the forms derived in this paper are not mathematical metrics. To avoid further confusion we will use the less precise terms distance function and similarity function in what follows; a nearest neighbor classifier chooses minimally distant or maximally similar database elements.

The main results of this paper are given by EQ-2, EQ-3 and EQ-4,5. Our similarity function is parameterized by a value $\alpha \in (0,1)$ and the first result is an exact closed form formula for its value as a function of $\alpha$. The second result is an approximation for small $\alpha$. The third is another kind of approximation which is presented because its derivation is, by comparison to the first two formulas, very brief.

Following derivation of these results, the notion of a stochastic equivalence predicate is introduced; it includes our first two main results as special cases. The fundamental differences between these predicates and traditional distance functions or metrics are at first conceptually confusing and troublesome, but a case is made that in some settings stochastic equivalence predicates are to be preferred.

Two Stage Generation

A Simple Starting Point

Assuming the vectors we observe are modeled well by a single normal density $N_{\mu,\Sigma}$, there are two equally valid generative interpretations. One might imagine that the vectors observed are:

• generated by mutating the mean vector $\mu$ according to the normal density $N_{0,\Sigma}$. By this we mean drawing from this zero mean normal density, and adding the result to $\mu$.

• generated by mutating some vector $c$ by the hidden normal process $N_{0,\Sigma_I}$, where $c$ is itself generated by mutating $\mu$ by a second hidden normal process $N_{\mu,\Sigma_C}$ such that $\Sigma_I + \Sigma_C = \Sigma$ - which we observe/estimate.

It is the second interpretation which we find interesting. We think of $\Sigma_C$ as generating class representatives while $\Sigma_I$ generates instances of each representative, i.e. the queries and database elements we observe.

Some other problem knowledge might be used to guess the nature of the $I$ process. For example, one might have access to a limited supply of vectors known to be generated from the same source. Another alternative is to simply assume that all admissible $I,C$ decompositions of $\Sigma$ are equally probable. By admissible we mean that both $I$ and $C$ are positive definite, and therefore correspond to non-degenerate normal densities. Then it may be shown using an elementary argument that the expected decomposition is just $I = C = \Sigma/2$. The argument is: $\Sigma = \Sigma_I + \Sigma_C$ $\rightarrow$ $(\Sigma_I+\Sigma_C)/2 = \Sigma/2$ $\rightarrow$ each pair $(\Sigma_I,\Sigma_C)$ may be written as $(\Sigma/2 + \Delta, \Sigma/2 - \Delta)$ for some matrix $\Delta$. But then $(\Sigma/2 - \Delta, \Sigma/2 + \Delta)$ also gives a valid pair. So the subset of ${\mathbb{R}}^{n^2}$ giving admissible $I$ (similarly $C$) matrices, is symmetrical about $\Sigma/2$ whence the assumption of a flat density yields $\Sigma/2$ as the expected value for both $I$ and $C$. Thus despite our general ignorance, the assumption of a certain flat density allows us to infer something of the nature of the $I$ process. ²

Given a query $Q$ and class representative $Y_i$, $N_{0,\Sigma/2}(Q-Y_i)$ then gives the probability of $Y_i$ generating $Q$, i.e. $\Pr(Q\vert Y_i)$. From the most likely $Y_i$, we may choose to immediately infer the identity of the query. Alternatively, we may compute a posteriori values $\Pr(Y_i\vert Q)$ given some prior on the $\{Y_i\}$, and make the decision accordingly. A flat prior corresponds to our choice of a maximal $\Pr(Q\vert Y_i)$. One might also use the original model to provide $\Pr(Y_i)$.

But there are two problems with this approach. First, we cannot directly observe class representatives. We see only the instances that result from the second stage of the process. Second, the argument above that justifies the choice of $\Sigma/2$ as both $\Sigma_C$ and $\Sigma_I$, does not agree with what we know about most problems. In particular, it is usually the case that the second process generates somewhat smaller changes than does the first.

We have seen that $0.5 \cdot \Sigma$ is in some sense a natural choice for both $\Sigma_I$ and $\Sigma_C$. To address the second problem above, we make the additional assumption that both $\Sigma_I$ and $\Sigma_C$ are proportional to $\Sigma$ and write $\Sigma_I = \alpha \cdot \Sigma$ and $\Sigma_I = (1-\alpha) \cdot \Sigma$. For notational convenience we will therefore sometimes write the $I$ process as $M^\alpha$ and the $C$ process as $M^{1-\alpha}$. The $\alpha = 0.5$ case is in some sense (however weakly) supported by the argument above. Other values of $\alpha$ have no such underlying argument. Our assumption of $\alpha$ proportionality is therefore best seen as a mathematical expedient that addresses the first problem while at the same time allowing us to later achieve a closed form solution for the similarity function we seek.

Addressing the first problem is the subject of the remainder of this section, leading eventually to our first main result.

The case we've just considered corresponds to a generalization of the technique used for example in [6] where inverse variances are used to weight Euclidean distance providing similarity judgments. This amounts to assuming a diagonal covariance matrix, then forming the vector $Q-Y$ and selecting the $Y$ that maximizes the probability of this difference given the zero mean normal density arising from this diagonal matrix. Weighted Euclidean distance results when one instead strives to minimize negative-logarithm of this probability. Covariances were later employed by others and amount to the technique above in the coordinate system established by the eigenvectors of the covariance matrix. A common rationale for such scaling is that the pattern recognizer should be oblivious to choice of units. So if one feature is measured in inches, and another feature with identical physical measurement error characteristics, is measured in millimeters, the pattern recognizer must automatically adapt. The thesis of this paper is that there is a deeper reason for such scaling, namely that observation of $I+C$ can sometimes teach us something about $I$.

It is a natural next step to assume instead that our data is modeled by some mixture of $k$ normal densities. After learning this mixture by some method (e.g. EM), we consider the problem of inferring a similarity function, but we begin by reviewing relevant definitions.

Preliminaries

Our observations are assumed to be elements of ${\mathbb{R}}^d$. Without loss of generality our notation will be restricted to zero-mean multi-dimensional normal densities defined by:

$$N_\Sigma(x) = \frac{1} {(2 \pi)^{d/2} \vert\Sigma\vert^{1/... ...Sigma^{-1} x} = \eta \cdot e^{\frac{1}{2} x^t \Sigma^{-1} x}$$

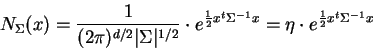
where for brevity's sake we've denoted the leading constant by $\eta$.

A normal mixture is then defined by $M = \{(c_k,\mu_k,N_{\Sigma_k})\}$ such that $c_k \geq 0, \sum_k c_k = 1, \mu_k \in {\mathbb{R}}^d$, and matrix $\Sigma_k \geq 0$, i.e. is a positive semi-definite operator. $M_k$ then refers to $(N_{\Sigma_k},\mu_k)$. We then write $\Pr(x\vert M_k) = N_{\Sigma_k}(x - \mu_k)$ and:

$$\Pr(x\vert M) = \sum_k c_k \cdot \Pr(x\vert M_k) = \sum_k c_k \cdot N_{\Sigma_k}(x-\mu_k)$$

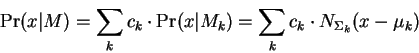
We will also make use of the following definite integral:

$$\int_{-\infty}^{+\infty} e^{-[u(x-a)^2 + v(x-b)^2 + w(x-c)^... ...v+acuw+bcvw)} {u+v+w} - {(a^2u+b^2v+c^2w)}}} {\sqrt{u+v+w}}$$ (1)

As this form is rather complex, we will denote its value $D(u,v,w,a,b,c)$ in the development that follows.

Shifting to an Eigenbasis

Each component $M_k$ is further resolved into an $I$ and $C$ portion denoted $M^I_k$ and $M^C_k$. By our proportionality assumption above $M^I_k = \alpha \cdot \Sigma_k$ and $M^C_k = (1-\alpha) \cdot \Sigma_k$, from which it follows that the eigenvectors of each $\Sigma_k^I$ are the same as those of $\Sigma_k^C$. We denote by $E_k$ the matrix whose columns are these eigenvectors. $\lambda^k_i$ then denotes the ith eigenvalue of $\Sigma_k^{-1}$. We then write $x^k_i$ to mean $(E_k^t x)_i$, i.e. the ith component of $x$ expressed in the Eigenbasis of $M_k$.

We may now compute $\Pr(x\vert M)$ in this Eigenbasis and enjoy the computational and mathematical convenience of diagonal covariance matrices:

$$\Pr(x\vert M) = \sum_k \left[ c_k \eta_k \prod_{i=1}^d e^{-\frac{1}{2} [x^k_i - (\mu_k)^k_i]^2 \lambda^k_i} \right]$$

The Joint Generation Process

Figure 1: The joint generation of a query $Q$ and database element $Y$ from a single hidden class representative $x$ which is itself generated from some $M_k$ - an element of a multi-dimensional normal mixture density, with mean $\mu _k$.

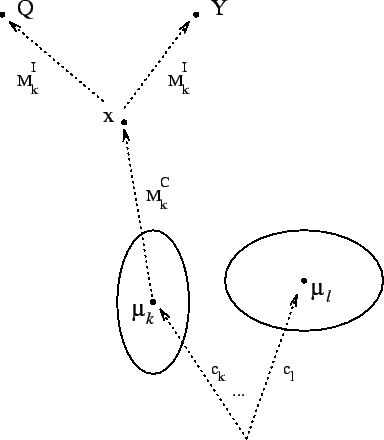
With reference to figure-1 we analyze the event consisting of the query $Q$ and a database element $Y$ being observations of a common class representative $x$, itself generated from $\mu _k$. In what follows, conditioning on our overall model of generation is implicit. We also remark that selection of a mixture element via the $c_k$ terms is assumed to be entirely part of the $C$ process. The probability of this event is given by:

$$\Pr(Q \cdot Y \cdot x \cdot \mu_k) = c_k \cdot \Pr(x-\mu... ...M^C_k) \cdot \Pr(Q-x\vert M^I_k) \cdot \Pr(Y-x\vert M^I_k)$$

So that:

$$\Pr(Q \cdot Y \cdot \mu_k) = \int_x c_k \cdot \Pr(x-\m... ...M^C_k) \cdot \Pr(Q-x\vert M^I_k) \cdot \Pr(Y-x\vert M^I_k)$$

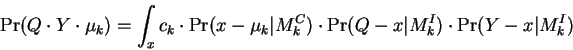
Now combining the three constant $\eta$ factors (within the $\Pr(\cdot)$ terms above) yields:

$$\eta_{k,\alpha} = \frac{1}{(2\pi)^{3d/2} \alpha^{2d} (1-\alpha)^d} \cdot \frac{1}{\vert\Sigma_k\vert^{3/2}}$$

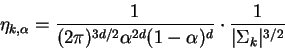
We then write:

$$\Pr(Q \cdot Y \cdot \mu_k) = c_k \cdot \eta_{k,\alpha} \c... ...Q-x)} \cdot e^{\frac{1}{2} (Y-x)^t {\Sigma^I_k}^{-1} (Y-x)}$$

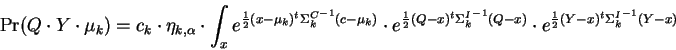
Shifting to an Eigenbasis transforms the above into:

$$\Pr(Q \cdot Y \cdot \mu_k) = c_k \cdot \eta_{k,\alpha} \cdot \prod_{i=1}^d \int_{-\infty}^\inf... ...cdot e^{-\frac{1}{2} [Y^k_i - x^k_i]^2 \frac{\lambda^k_i}{\alpha}} \cdot dx_i^k$$

$$= c_k \cdot \eta_{k,\alpha} \cdot \prod_{i=1}^d \int_{-\infty}^\inf... ... Q^k_i)^2 + \frac{\lambda^k_i}{2\alpha} (x^k_i - Y^k_i)^2 \right]} \cdot dx_i^k$$

where it has been possible to reorder the product and integral operators because in the Eigenbasis, each dimension corresponds to an independent term. The form of EQ-1 is readily recognized and we have the result:

$$\Pr(Q \cdot Y \cdot \mu_k) = c_k \cdot \eta_{k,\alpha} \c... ...{\lambda^k_i}{2\alpha}, (\mu_k)^k_i, Q^k_i, Y^k_i \right)$$

Finally, summing over the models in the mixture yields one of the main results of this paper:

Main Result 1  

$$\Pr(Q \cdot Y ) = \sum_k \left[ c_k \cdot \eta_{k,\alpha... ...k_i}{2\alpha}, (\mu_k)^k_i, Q^k_i, Y^k_i \right) \right]$$ (2)

which is a closed form exact solution for the joint probability we seek, given the assumptions we've made. We have therefore succeeded in dealing with the fact that class representatives are hidden, by simply integrating over all possibilities.

To effect classification, we select a database element $Y_i$ maximizing $\Pr(Y_i\vert Q)$. But this conditional density is just $\Pr(Q \cdot Y_i) / \Pr(Q)$ and the denominator is constant for each query. So we might as well simply maximize the joint probability.

Our computation of $\Pr(Q \cdot Y)$ above is performed in the Eigenbasis of each mixture component, i.e. in terms of the $\{Q^k_i\}$, $\{Y^k_i\}$ and $\{(\mu_k)^k_i\}$. The $\{Q^k_i\}$ must be computed for each new query, but the others may be precomputed trading a modest amount of space for considerable time savings.

Approximate Forms

The small $\alpha$ case

We will show that the assumption of small $\alpha$ leads to a simpler form of EQ-2. Our first step is to re-express each of the four sub-terms of EQ-1 under this assumption. For brevity we focus on a particular value for $i$ and $k$ and therefore omit subscripts and superscripts:

$$u + v + w = \frac{\lambda}{2} \left( \frac{1}{1-\alpha} + \frac{2}{\alpha} \right) \approx \frac{\lambda}{\alpha}$$

$$a^2u+b^2v+c^2w \approx \frac{\lambda}{2\alpha}(Q^2+Y^2) + \frac{\lambda}{2} \mu^2$$

$$a^2u^2+b^2v^2+c^2w^2 \approx \frac{\lambda^2}{4\alpha^2}(Q^2+Y^2) + \frac{\lambda^2}{4} \mu^2$$

$$2(abuv+acuw+bcvw) \approx \frac{\lambda^2}{4\alpha^2}(2QY) + \frac{\lambda^2}{4}\left( \frac{2 \mu Q}{\alpha} + \frac{2 \mu Y}{\alpha}\right)$$

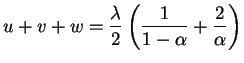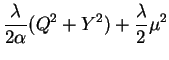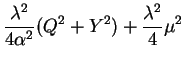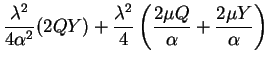Before making the substitutions above, one must modify the argument of the exponential in EQ-1 so that the second term shares a common denominator. This is accomplished by multiplying it by $u+v+w$ in exact form. Then the approximations above may be made and we are led to:

$$\Pr(Q \cdot Y \cdot \mu_k) \approx c_k \cdot \eta_{k,\alpha... ... + \frac{-\lambda}{2}(\frac{Q^k_i+Y^k_i}{2} - (\mu_k)^k_i)^2}$$

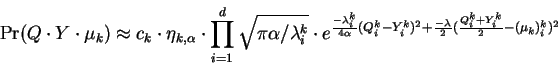
Now simplifying and rearranging constants while shifting out of the Eigenbasis and summing over mixture components leads to:

$$\Pr(Q \cdot Y) \approx \frac{1}{\alpha^d} \sum_k c_k \cdot N_{2\alpha\Sigma_k}(Q-Y) \cdot N_{\Sigma_k}((Q+Y)/2 - \mu_k)$$

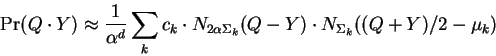
Shifting to probability notation yields the second main result of this paper:

Main Result 2  

$$\Pr(Q \cdot Y) \approx \frac{1}{\alpha^d} \sum_k c_k \Pr(Q-Y\vert M_k^{2\alpha}) \cdot \Pr((Q+Y)/2\vert\bar{M}_k^1)$$ (3)

where equality holds in the limit as $\alpha$ approaches zero. For clarity we've adjusted our notation slightly so that the superscript of $M$ refers to the selected $\alpha$ factor, and a bar above $M$ indicates that the model has a non-zero mean vector which is understood to be subtracted.

As $\alpha$ approaches zero, the first probability term becomes dominant so that $\Pr(Q \cdot Y)$ in the limit depends only on the vector difference $Q-Y$. Moreover the sum over components may be thought of as approximately a maximum selector since with models such as these, a single component usually dominates the sum. So the corresponding simplified classification rule amounts to ``maximize over database elements $Y$ and mixture components $M_k$ the probability $\Pr(Q-Y\vert M_k)$.'' We do not advocate this rule in part because the assumption of vanishingly small $\alpha$ is both unnatural, and makes our inference of the $I$ process from the observed samples, even more tenuous. We therefore suggest that EQ-3 is best applied for small, but not vanishingly small $\alpha$ values.

Simpler Derivations

The intricate mathematics of earlier sections addresses the fact that the queries $Q$ we receive and database elements $\{Y_i\}$ we observe are not class representatives - but are themselves the result of class and instance generation processes.

Assuming instead that either the query or database elements are class representatives, one is led very quickly to simpler forms. Despite the less than satisfactory nature of this assumption, we present them because of their simplicity, and because they were the starting point of the author's work. In a sense, the complex earlier sections are the author's attempt to deal with the conceptual problems associated with these early discoveries. It is worth noting that however flawed conceptually, these forms perform very well in limited experiments [7].

Assuming alternately that the queries $Q$ are class representatives, or that the database elements $\{Y_i\}$ are, yields the two forms:

Main Result 3  

$$\Pr(Q \cdot Y) = \sum_k \Pr(Q-Y\vert M^I_k) \cdot \Pr(Q\vert M^C_k) \cdot \Pr(M_l^C)$$ (4)

$$\mbox{(or)}$$

$$\Pr(Q \cdot Y) = \sum_k \Pr(Q-Y\vert M^I_k) \cdot \Pr(Y\vert M^C_k) \cdot \Pr(M_l^C)$$ (5)

It is interesting to note that EQ-3 in a sense interpolates between these two by computing $\Pr(\frac{Q+Y}{2}\vert M^C_k)$.

If computational effort must be minimized, EQ-5 is preferred since the $\Pr(Y\vert M^C_k)$ can be precomputed for each database element. Operating in an Eigenbasis is not necessary, but as before will contribute significant additional time savings. EQ-4,5 are included as main results of the paper because of their simplicity and particular computational economy. While they do not specify the nature of the $I$ and $C$ processes, we suggest that the assumption of earlier sections that $M^I_k = M^{\alpha}_k$ and $M^C_k = M^{1-\alpha}_k$ are reasonable starting points and that the neutral value $\alpha=\frac{1}{2}$ should be tried first.

We now describe a variation on EQ-5 which can yield additional computational time savings. Converting to to conditional form yields:

$$\Pr(Q\vert Y) = \sum_k \Pr(Q-Y\vert M_k^I) \cdot \Pr(M_k^C\vert Y)$$

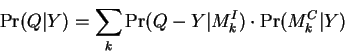
where:

$$\Pr(M_k^C\vert Y) = \frac{\Pr(Y\vert M_k^C) \Pr(M_k^C)} {\sum_i \Pr(Y\vert M_i^C) \Pr(M_i^C)} \nonumber$$

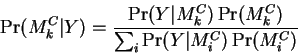
Here the database search seeks to maximize $\Pr(Q\vert Y)$ rather than $\Pr(Y\vert Q)$. Over short ranges however we expect that $\Pr(Y\vert Q) \approx \Pr(Q\vert Y)$ and therefore tolerate this reformulation of the problem. The next practical expedient consists of recording for each database element the component $k$ for which this quantity is maximized and assuming all others to be zero [7]. This amounts to precomputed hard vector quantization of the database. We are then left to deal with only a single mixture component for each database record. Additional savings are possible by passing to logarithms leaving what amounts to a weighted Euclidean distance computation and addition of a constant factor.

Metric Properties and the
``Self Recognition'' Paradox

As remarked earlier, the main results of this paper are not metrics in the accepted mathematical sense. Metrics $d(\cdot,\cdot)$ are usually understood to be non-negative real valued functions of two arguments which obey three properties: i) $d(x,y) = 0$ iff $x=y$, ii) $d(x,y) = d(y,x)$, and iii) $d(x,z) \leq d(x,y) + d(y,z)$. We have used the term because it more generally means a measurement of some quantity of interest - in our case the probability that $Q$ and $Y$ are instances of some single third element $X$ given appropriate models for the generation of class representatives, and instances thereof.

To avoid future confusion, we propose the following definition which represents a further abstraction of the setting from earlier sections:

Definition 1   The statement that a joint probability density $\Pr(X \cdot Y)$ is a stochastic equivalence predicate means that there exists a density $\Pr(s)$, and conditional density $\Pr(t\vert s)$ such that:

$$\Pr(X \cdot Y) = \int \Pr(X\vert s) \cdot \Pr(Y\vert s) \cdot \Pr(s) \cdot ds$$

Density $\Pr(s)$ is thought of as generating class representatives, while $\Pr(t\vert s)$ models the observation of class instances.

Our development based on normal mixtures involves a two stage class generation process. Thus we have a density $\Pr(s)$, conditional density $\Pr(r\vert s)$, and conditional density $\Pr(t\vert r,s)$ such that:

$$\Pr(X \cdot Y) = \int \Pr(X\vert r,s) \cdot \Pr(Y\vert r,s) \cdot \Pr(r\vert s) \cdot \Pr(s) \cdot dr \cdot ds$$

This is easily recognized as a special case of the definition above.

Stochastic equivalence predicates in general, and our formulations in particular are certainly non-negative real valued functions of two arguments, and enjoy the symmetry property (item ii above). But that's where the agreement ends. They do not satisfy the triangle inequality (item iii) but more importantly they do not satisfy item ``i'' which we term the self-recognition axiom.

Superficially there is a problem of polarity, which is solved by considering either $1 - \Pr(Q \cdot Y)$ or the logarithmic form. But then would hope that $\Pr(X \cdot X)$ would equal unity - having logarithm zero. Unity however is not the value assumed and we might then consider somehow normalizing $\Pr(X \cdot Y)$ by say $\Pr(X)$ or some combination with $\Pr(Y)$ in order to rectify the situation. Unfortunately any such strategy is doomed because of the following observation: Viewing $Y$ as a free variable, $\Pr(X \cdot Y)$ does not necessarily assume its maximal value when $X = Y$. ³

This is at first a deeply troubling fact. Other investigators have employed distance functions which do not obey property iii above, and symmetry is sometimes abandoned. But self-recognition is somehow sacred. If our distance functions are in any sense an improvement, then we are presented with:

The ``self recognition'' paradox: the better distance function
may have the property that there are queries $Q$ which do not
recognize themselves, i.e. even if $Q$ is in the database,
some other element $Y$ may be preferred.

The paradox is resolved through better understanding the quantity that the stochastic equivalence predicates measure with particular emphasis on the assumption that $Q$ and $Y$ represent independent observations.

Recall that our model imagines $Q$ and $Y$ to be noisy observations (instances) of some hidden object $X$, which may be thought of as a platonic ideal. We also assume a probability model⁴ for these ideals $X$ and a second model for the generation of noisy observations of $X$. It is crucial to observe that we also assume that the observation of $Q$ and $Y$ are independent events. So having fixed $X$, and assuming that $Q$ is a somewhat noisy image of it with correspondingly low probability $p$, the fact that $Q$ may equal $Y$ is not a remarkable event and the probability of observing them both conditioned on $X$ is just $p^2$.

An example serves to better illustrate this point. Imagine listening to music broadcast by a distant radio station. If the same song is played twice, we hear two different noise corrupted versions of the song. A reasonable but crude model of music would expect locally predictable signals and would therefore assign somewhat higher probability to the original than to noisy versions. Now let $S$ be the original recording of a song as broadcast from the station, and suppose that we hear on a particular day a very noisy version $Q$. Further suppose that over time we have assembled a database of music as recorded from this distant station. Assume the database contains a version $V$ of $S$ recorded on an earlier day on which favorable atmospheric conditions prevailed resulting in an almost noiseless version. Now given any reasonable model for noise we would expect that the probability of $Q$ given $S$ to be far less than the probability of $V$ given $S$. But then:

$$\Pr(Q \cdot Q \cdot S) = \Pr(Q\vert S) \cdot \Pr(Q\vert S) \cdot \Pr(S)$$

$$\leq \Pr(Q\vert S) \cdot \Pr(V\vert S) \cdot \Pr(S)$$

$$= \Pr(Q \cdot V \cdot S)$$

whence a search of the database using our stochastic equivalence predicate would choose $V$ even if $Q$ itself is present.⁵

To recapitulate: stochastic equivalence predicates attempt to measure the probability that two observations have a common hidden source not how much they differ. This objective leads to distance functions which do not have the self-recognizing property but are nevertheless better to the extent that their constituent models correspond to nature.

We now endeavor to illuminate the relationship between our model and the argument above to the traditional nearest neighbor outlook⁶. To begin consider EQ-4 which was derived under the assumption that the queries are class representatives (not noisy observations thereof). Notice that $\Pr(Q-Y\vert M^I_k)$ is maximized when $Q=Y$ and that the other two terms do not depend on $Y$. So this form does have the self recognizing property. The same is not necessarily true of EQ-5.

One may then reconcile the conventional nearest neighbor outlook with this paper's framework by adding the assumption that the queries are class representatives. Unfortunately for some problems this is almost certainly false and the conventional nearest neighbor approach is simply flawed. Another approach one might take is to define two conditional models, one for queries and one for database elements since the nearest neighbor approach seems to implicitly assume that queries are in essence noiseless observations of class representatives. We will however not develop this approach in this paper.

So to the extent that we can accurately model platonic ideals and observation noise, we submit that that stochastic equivalence predicates are asking the right question and conventional metrics the wrong one.

Discussion - A Range of Behavior

We view our approach as a form of unsupervised metric learning - although as we have seen, we do not obtain a metric in the mathematical sense. From the statistical viewpoint our approach is a way to obtain a joint density from a simple density plus strong additional assumptions.

If the mixture contains a single component, our methods correspond to the well known heuristic technique of employing weighted Euclidean distances - with the weights inversely proportional to the feature variances.⁷

If the number of elements in the mixture is equal to the number of classes, then our approach tends (at least conceptually) to the traditional Mahalanobis distance method given sufficient data. We will now sketch the intuition behind this observation. If many examples of each class are available, then the mixture density learned will plausibly have a term for each class. Focusing on EQ-5 because it is easiest to interpret, and on a database element $Y$ which lies very near to the mean of its class, we might hope that $\Pr(M_k^C\vert Y)$ is greatest for the class to which $Y$ belongs - and imagine it to be unity. Also $\Pr(Q-Y\vert M^I_k) \approx \Pr(Q-\mu_k\vert M^I_k)$ since we've assumed $Y \approx \mu_k$. So we might reasonably expect a nearest neighbor search of the $Y$ which are near to their class means to yield roughly the same result as a traditional Mahalanobis Distance method. Finally we might hope the the presence of other members of the class in the database will in general help - not hurt classifier performances.

If the number of elements in the mixture is intermediate between these two extremes, the elements represent super-classes of those we're interested in. Of primary interest we feel, is this intermediate region in which a more effective distance function might be discovered by uncovering hidden structure in the data.

As the database grows one may increase the number of mixture elements so that our scheme spans the entire spectrum from a starved starting point in which one can expect to have only a single representative of each class, to the data-rich extreme in which many exist.

Regarding our $\alpha$ parameter, we remark that it should be thought of as domain dependent. However values very near to zero create conceptual difficulties⁸, since they correspond to $I$ processes which generate vanishingly small variations on a class representatives. The problem is that our assumption that we can infer anything of the $I$ process as $\alpha$ approaches zero becomes increasingly tenuous.

In this paper we've presented only one approach to inference. Strong assumptions were made so that a closed form solution would result. More sophisticated approaches represent an interesting area for future work. Given some prior knowledge of the $I$ and $C$ processes one might strive to compute posteriori structures. Or one might have access to a supply of instance pairs known to have been generated by the same class representative - and somehow use this information to advantage. Finally this work might be extended to the supervised case in which class or superclass labels are available.

Model Issues

In this section we remark on several matters of practical importance and suggest simple solutions. They relate the problems associated with estimating the parameters of complex models such as the multidimensional normal mixtures we rely on - and to our choice of Gaussian densities.

The Number of Mixture Components

In our development so far, we have assumed that the number $k$ of elements in the normal mixture was somehow given. In practice it is difficult to decide which value is best. The approach we prefer begs this question by instead starting with a prior on a range of possible values and combining the results of all the models. If $M(n)$ denotes a mixture model with $n$ elements, then this amounts to computing:

$$\Pr(Q \cdot Y) = \sum_n \Pr(Q \cdot Y\vert M(n)) \cdot \Pr(M(n))$$

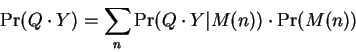
In one experiment [7], this blended distance performed as well as the single best value. Assuming a flat prior and passing to logarithms, we remind the reader that this blend is well approximated by the $\min$ operation, i.e. by choosing the shortest code-length.

Covariance Estimation

Our discussion above has avoided the details of learning the necessary mixture density, and in fact not mentioned the delicate matter of estimating the parameters of a single multivariate normal density given little data. We therefore comment that in practice one may use the well known Expectation Maximization (EM) method to obtain a (locally) maximum-likelihood mixture model. In this case as well as with a single density, some form of statistical flattening is advisable if little data is available. In this section we briefly describe practical techniques for dealing with this issue.

One convenient statistical device amounts to believing the variances before the covariances. One multiplies the off-diagonal entries of $\Sigma$ by some scaling factor $s \in [0,1)$. Avoiding unity has the additional advantage of preventing ill-conditioned matrices (assuming none of the variances are near zero). This is discussed in greater detail in [7].

It should be mentioned that given enough data one might attempt to assign different values of $s$ to each mixture component. Intuitively this makes sense since some components may have many members while others have relatively few. Those with many members might be expected to work well with $s$ values closer to unity.

Functions with Bounded Support

It is worthwhile noting that in cases where the feature vectors have finite support, e.g. each feature is contained in say the unit interval, one should instead consider estimating the parameters of a mixture of multi-dimensional beta densities. Liporace [8] demonstrates that this introduces only small complications for a somewhat general class of densities.

A Simple Example

Consider a two dimensional distribution made up of two zero mean normal densities, of equal probability, but with covariance matrices which result in ellipsoidal contours that are very different. In particular, the principal axis of each are 90 degrees apart. Also, one has a small minor axis, while the other is closer to circular. Assume that each corresponds to items of a given class. Then it is not too great a challenge for mixture density estimators to discover this structure without the labels. The stochastic equivalence predicates described in this paper will then give rise to a very different decision boundary than would result from say simple Euclidean distance. This example also illustrates that the mixture components discovered might have identical means but very different covariance matrices.

The example above might of course have been dealt with using other methods since it has a simple discrete two class structure. More interesting examples would exhibit a continuous class structure corresponding to some continuous parameter such as age. Here our discrete mixture would attempt to approximate this continuous variation by covering various regions with different normal densities.

A Neural Network Application

Encoder nets⁹ [9] are feed-forward neural networks which include a highly constricted layer - forcing the network to somehow compress/encode its inputs and then decompress/decode them to arrive at an output which approximates the inputs. This well known design approach is an effective way to avoid over-training.

Our focus is on the constricted layer only. Each input vector presented to the network gives rise to some pattern of activations at this layer. Considering this pattern as real vector, we then suggest that the methods of this paper can be applied to learn a distance function for this space of activation patterns.

So given two inputs $X,Y$ to the network giving rise to encodings $E(X)$, $E(Y)$, we might compute a distance between them. This distance can then be used to effect classification via nearest neighbor search of some labeled dataset. Thus after training, the final stages of the network can essentially be discarded.

There is some evidence that this general approach is effective. In [10] a neural net the authors call LeNet-4 was trained to achieve 1.1% classification error for the problem of handwritten digit recognition. The authors realized that a particular 50-unit layer might be thought of as a feature vector, and built a pattern classifier using the Euclidean distance metric. The resulting system achieved the same 1.1% error level. What isn't clear from their work is whether the more complex forms of this paper could have improved performance further. If the activation vector is described well by a single normal density with covariance proportional to the unit matrix, then we would expect Euclidean distance to be essentially optimal. If however structure is evident in a sample of the space of such vectors, it may be that our methods can be used to advantage.

We speculate that it might also be possible to influence training so as to prefer networks having simple statistics in their encoder layer. In addition to simplifying later distance computations, this might have a positive impact on the network itself.

Possible Applications

Common front end signal processing in speech recognition systems reduces signal windows to feature vectors of dimension 10-20. It would be interesting to explore the application of unsupervised metric learning in general, and our stochastic equivalence predicates in particular, to this setting since the data are not conveniently labeled. Many other applications might benefit from our techniques. These include almost any problem for which nearest neighbor search is somewhat effective.

Common front end signal processing in speech recognition systems reduces signal windows to feature vectors of dimension 10-20. It would be interesting to explore the learning of stochastic equivalence predicates for this space since the data are not conveniently labeled. Many other applications might benefit from our techniques. These include almost any problem for which nearest neighbor search is somewhat effective.

Acknowledgments

The author thanks Ingemar Cox and David Jacobs for helpful discussions. Our joint work on face recognition from feature vectors [11] provided much needed concrete examples from which the author drew the intuition needed to complete this work. This work now continues with the authors above as well as Joumana Ghosn [7]. I thank Adam Grove and Steve Omohundro for helpful discussions and comments on earlier drafts. I also thank Eric S. Ristad. Our joint work on handwriting recognition and stochastic modeling contributed greatly to my thinking in this area.

Bibliography

1

R. O. Duda and P. E. Hart, Pattern Classification and Scene Analysis.
John Wiley & Sons, Inc., 1973.

2

R. D. Short and K. Fukunaga, ``The optimal distance measure for nearest neighbor classification,'' IEEE Transactions on Information Theory, vol. 27, September 1981.

3

K. Fukunaga and T. E. Flick, ``An optimal global nearest neighbor metric,'' IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 6, May 1984.

4

J. H. Friedman, ``Flexible metric nearest neighbor classification,'' tech. rep., Stanford University, Dept. of Statistics, 1994.

5

D. G. Lowe, ``Similarity metric learning for a variable-kernal classifier,'' Neural Computation, vol. 7, pp. 72-85, 1995.

6

T. Kanade, Computer Recognition of Human Faces.
Birkhäuser Verlag, Stuttgart Germany, 1977.

7

I. J. Cox, J. Ghosn, and P. N. Yianilos, ``Experiments on feature-based face recognition using gaussian models and mixtures,'' tech. rep., The NEC Research Institute, Princeton, New Jersey, 1995.

8

L. R. Liporace, ``Maximum likelihood estimation for multivariate observations of markov sources,'' IEEE Transactions on Information Theory, vol. 28, pp. 729-734, 1982.

9

D. H. Ackley, G. E. Hinton, and T. J. Sejnowski, ``A learning algorithm for boltzmann machines,'' Cognitive Science, vol. 9, pp. 147-169, 1985.

10

L. Bottou, J. Denker, H. Drucker, I. Guyon, L. Jackel, Y. LeCun, U. Müller, E. Säckinger, P. Simard, and V. Vapnik, ``Comparison of classifier methods: A case study in handwritten digit recognition,'' in Proc. 12th IAPR International Conference on Pattern Recognition, April 1993.

11

I. J. Cox, P. N. Yianilos, S. L. Hingorani, and D. W. Jacobs, ``Experiments on feature-based face recognition,'' tech. rep., The NEC Research Institute, Princeton, New Jersey, 1995.

About this document ...

Metric Learning via Normal Mixtures

This document was generated using the LaTeX2HTML translator Version 2K.1beta (1.47)

Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.

The command line arguments were:
latex2html -split 0 -image_type gif -nonext_page_in_navigation -noprevious_page_in_navigation -up_url ../main.html -up_title 'Publication homepage' -numbered_footnotes mlnm.tex

The translation was initiated by Peter N. Yianilos on 2002-07-03

Footnotes

... Yianilos¹

NEC Research Institute Technical Memorandum: 4 Independence Way, Princeton, NJ 08540 - pny@research.nj.nec.com

... process.²

It is worthwhile noting that it is only because we've assumed in our second generative interpretation that both the $I$ and $C$ processes are normal, that we can conclude that the expected distributions are themselves normal. Without this assumption we have made a statement only about the covariances of these expected distributions, and said nothing of their form.

.... ³

With reference to EQ-2 let $d=1$ and focus on only the $D$ term since the leading terms are constant. Let $\lambda = 1, \alpha = 0.1, \mu = 0, q = 1, y = 1$. The result is $D \approx 0.3223$. Now set $y = 0.9$ leaving the other values unchanged. The result is $D \approx 0.3309$ which exceeds the first value. So moving $y$ away from $q$ towards $\mu$ improved the joint probability. Continuing the motion until $y = 0.8$ restores the probability to its original value, and continued motion results in further declines. So there exists a region about $q$, oriented towards the origin, which is preferred to $q$. The size of this region is a function of $\alpha$ with small values corresponding to small regions.

... model⁴

For simplicity we'll ignore the superclass model from the definition. In the case of Gaussian mixtures, this amounts to assuming a mixture with one component.

... present.⁵

We've glossed over for simplicity's sake the fact that the stochastic equivalence predicate is actually defined in terms of an integral over $X$.

... outlook⁶

By this we mean the use of a conventional metric, or a distance function having the self-recognition property.

... variances.⁷

One may also shift to an Eigenbasis so that covariances are considered.

... difficulties⁸

A point also made earlier in the paper

... nets⁹

Also known as Auto-Association Networks, or M-N-M Encoders