Leonid Gurvits and Peter N. Yianilos
(Extended Abstract)1
May, 1998
Keywords: Semidefinite programming, Maximum cut (MAX CUT ) problem, maximum entropy, maximum determinant completion, Bregman distance, Kullback-Leibler distance, normal (Gaussian) density, Sinkhorn iteration.
Semidefinite programming has emerged as an important and
practical optimization framework that is increasingly relevant
to combinatorial problems. Given symmetric matrices ![]() and
and
![]() , and vector
, and vector ![]() , the objective is to minimize
, the objective is to minimize
![]() subject to
subject to
![]() and
and ![]() .
.
There has been a great deal of recent work on the solution of
semidefinite programming problems. The ellipsoid method
together with a separation oracle due to Lo![]() asz may be
used; and the work of Nesterov and Nemirovsky [21] and
Alizadeh [2] adapts the interior-point method to
the task.
asz may be
used; and the work of Nesterov and Nemirovsky [21] and
Alizadeh [2] adapts the interior-point method to
the task.
The connection between semidefinite programming and
combinatorial optimization was first established by Lo![]() asz
in [17] and later by Lo
asz
in [17] and later by Lo![]() asz and Schrijver in
[18].
asz and Schrijver in
[18].
Goemans and Williamson [12] discovered a semidefinite
programming relaxation of the NP-hard MAX CUT problem, which
generates cuts with weight no less than
![]() of
optimal. Other optimization problems have been considered
using essentially the same approach.
of
optimal. Other optimization problems have been considered
using essentially the same approach.
For MAX CUT their method begins by constructing the symmetric
weighted adjacency matrix ![]() for the graph
for the graph ![]() under
consideration. We denote by
under
consideration. We denote by ![]() the number of vertices in
the number of vertices in ![]() , and
by the
, and
by the ![]() the number of edges.
The semidefinite programming problem is then
to find matrix
the number of edges.
The semidefinite programming problem is then
to find matrix ![]() that minimizes
that minimizes ![]() subject to
subject to ![]() and
and
![]() . This matrix is then
factored as
. This matrix is then
factored as ![]() using, for example, Cholesky
decomposition. Given a vector
using, for example, Cholesky
decomposition. Given a vector ![]() they interpret the sign
pattern of
they interpret the sign
pattern of ![]() as a cut -- and show that for uniform random
as a cut -- and show that for uniform random ![]() the expected value of this cut is at least
the expected value of this cut is at least
![]() times the weight of a maximum cut. It is easy to see
that instead of uniform random
times the weight of a maximum cut. It is easy to see
that instead of uniform random ![]() one can use a Gaussian
vector
one can use a Gaussian
vector ![]() with unit covariance matrix. Also, since only
the distribution of the sign pattern matters it is enough
to get
with unit covariance matrix. Also, since only
the distribution of the sign pattern matters it is enough
to get ![]() to within a diagonal factor, i.e.
to within a diagonal factor, i.e. ![]() ,where
,where ![]() is
a diagonal positive-definite matrix.
is
a diagonal positive-definite matrix.
This approach and the general connection of semidefinite programming to combinatorial optimization is surveyed in [11]. An alternative solution approach is given by Klein and Lu [15] based on the power-method. Benson Ye and Zhang describe a dual scaling algorithm and report on experiments for semidefinite programs arising from instances of MAX CUT [3]. The MAX CUT problem is surveyed in [22].
This paper introduces the deflation-inflation algorithm
and outlook for certain convex optimization problems including
those arising from the MAX CUT relaxation above.
Applied to MAX CUT the algorithm is quite simple. It
begins by choosing diagonal values for ![]() so that
so that ![]() .
We solve an approximation to the semidefinite program and next
choose
.
We solve an approximation to the semidefinite program and next
choose ![]() to select the desired precision.
to select the desired precision.
In each cycle of the algorithm the diagonal entries of ![]() are modified one-by-one, i.e. for each iteration only one diagonal
entry is changed. The update rule is:
are modified one-by-one, i.e. for each iteration only one diagonal
entry is changed. The update rule is:
The algorithm terminates when each ![]() is equal to
is equal to
![]() within some error tolerance.
Notice that the algorithm is essentially searching over the
space of diagonal values for
within some error tolerance.
Notice that the algorithm is essentially searching over the
space of diagonal values for ![]() .
.
We show that the algorithm above converges to a unique
solution, and that this approximates well the original
problem. Our analysis further establishes local linear
convergence under rather general circumstances - and global
convergence after
![]() diagonal
updates given a form of the algorithm that chooses diagonal
elements greedily. The local analysis and portions of
the global analysis apply to the well-studied Sinkhorn
balancing problem [23] and seems relevant to the
recent matching work of Linial, Samorodnitsky and Widgerson
[20]. Our global analysis is the first we are aware of
for projection methods of this general class, which includes
the celebrated expectation maximization (EM) algorithm
[9].
diagonal
updates given a form of the algorithm that chooses diagonal
elements greedily. The local analysis and portions of
the global analysis apply to the well-studied Sinkhorn
balancing problem [23] and seems relevant to the
recent matching work of Linial, Samorodnitsky and Widgerson
[20]. Our global analysis is the first we are aware of
for projection methods of this general class, which includes
the celebrated expectation maximization (EM) algorithm
[9].
The critical operation in each update is
![]() . Notice that only one element of
. Notice that only one element of
![]() is examined. The operation then amounts to solving a
system of linear equations. So when
is examined. The operation then amounts to solving a
system of linear equations. So when ![]() has special
structure, or is sparse, specialized statements about the
algorithm's complexity can be made. When these systems are
large and can be rapidly solved, our method may be the best
available.
has special
structure, or is sparse, specialized statements about the
algorithm's complexity can be made. When these systems are
large and can be rapidly solved, our method may be the best
available.
In the sparse case it is interesting to note that our basic
algorithm is linear space, i.e. ![]() .
.
We have implemented our algorithm for MAX CUT using
Gauss-Seidel iteration with successive over-relaxation to solve
the linear systems [8]. To avoid inverting the
resulting ![]() and performing Cholesky decomposition, we
instead compute
and performing Cholesky decomposition, we
instead compute ![]() as a power series. For sparse
constant degree random graphs our analysis suggests that this
overall method should scale roughly as
as a power series. For sparse
constant degree random graphs our analysis suggests that this
overall method should scale roughly as ![]() and our
experiments confirm this. The full paper describes this
implementation and our experimental results.
and our
experiments confirm this. The full paper describes this
implementation and our experimental results.
Recall that the starting matrix ![]() is essentially a
combinatorial object representing the weighted adjacency of
graph nodes. After the algorithm runs, modifying only its
diagonal entries,
is essentially a
combinatorial object representing the weighted adjacency of
graph nodes. After the algorithm runs, modifying only its
diagonal entries, ![]() is the matrix
is the matrix ![]() we seek. An
interesting aspect of this work is that a probabalistic
viewpoint is of utility when addressing this essentially
combinatorial problem. We view
we seek. An
interesting aspect of this work is that a probabalistic
viewpoint is of utility when addressing this essentially
combinatorial problem. We view ![]() as the covariance matrix
associated with a normal density, and
as the covariance matrix
associated with a normal density, and ![]() gives its inverse
covariance. It is easily verified that the random cuts are
then just sign patterns from random vectors drawn from this
density.
gives its inverse
covariance. It is easily verified that the random cuts are
then just sign patterns from random vectors drawn from this
density.
Each step in our algorithm corresponds to a projection operation with respect to Kullback-Leibler distance [16,6] under Bregman's general framework for convex optimization [5]. This framework is closely related to the later work of I. Csiszár and G. Tusnády [7] and generalizes much the earlier work [1,19] and also [10,4].
Our main computational focus in this paper is on the semidefinite programming problem corresponding to MAX CUT relaxation, i.e. with diagonal constraints. Another class of problems which allows basically the same complexity and convergence analysis corresponds to block-diagonal positive-definite constraints. The case of two complimentary block-diagonal constraints can be solved using Singular Value Decomposition, while our method in this case is a Riccati-like iteration. We believe that beyond two block-diagonal constraints that our method is the best currently available practical method for large problems.
Another application of our method is the efficient solution of matrix completion problems [13]. Here the objective is to find the maximum determinant positive matrix with specified values on and near to its diagonal. This corresponds to finding the maximum entropy normal density having prescribed marginal distributions.
Finally, we want to clarify one important historical point:
our choice of a barrier
![]() was motivated by
Bregman's seminal paper [5]. In a discrete
setting this approach also has many merits, but lacks the
crucial property self-concordance [21]
property. But in the Gaussian case this barrier is (basically
Bregman's) is a sense optimal [21]. This celebrated
self-concordance property has been studied in the context of
Newton-like methods. We used it to analyze the convergence of
our projection-like method.
was motivated by
Bregman's seminal paper [5]. In a discrete
setting this approach also has many merits, but lacks the
crucial property self-concordance [21]
property. But in the Gaussian case this barrier is (basically
Bregman's) is a sense optimal [21]. This celebrated
self-concordance property has been studied in the context of
Newton-like methods. We used it to analyze the convergence of
our projection-like method.
Given a joint probability distribution ![]() on a product
space
on a product
space ![]() , and another distribution
, and another distribution ![]() defined on
defined on
![]() alone, we define a new distribution
alone, we define a new distribution
![]() , which inherits as much as possible
from
, which inherits as much as possible
from ![]() while forcing its
while forcing its ![]() -marginal to match
-marginal to match ![]() . The
focus of our paper is exposing certain properties and
algorithms relating to this natural operation in which a joint
distribution is deflated via conditionalization, and
then reinflated by multiplication to exhibit some
required marginal.
. The
focus of our paper is exposing certain properties and
algorithms relating to this natural operation in which a joint
distribution is deflated via conditionalization, and
then reinflated by multiplication to exhibit some
required marginal.
We denote by ![]() the
the ![]() -marginal of
-marginal of ![]() , i.e.
, i.e.
![]() . Similarly we denote by
. Similarly we denote by ![]() the function
the function ![]() , i.e. the conditional probability of
, i.e. the conditional probability of ![]() given
given ![]() .
Next, given distribution
.
Next, given distribution ![]() on
on ![]() and denoting it
and denoting it ![]() we define the operator:
we define the operator:
which transforms ![]() into a new distribution whose
into a new distribution whose ![]() -marginal
is exactly
-marginal
is exactly ![]() .
.
Among all distributions having this marginal, ![]() is
special in as much as no other such distribution is closer to
is
special in as much as no other such distribution is closer to
![]() under the Kullback-Leibler (KL) distance [16,6]
denoted
under the Kullback-Leibler (KL) distance [16,6]
denoted
![]() . That is,
. That is, ![]() is a projector with respect to KL-distance and the set of
distributions with
is a projector with respect to KL-distance and the set of
distributions with ![]() -marginal
-marginal ![]() . This is formalized by:
. This is formalized by:
proof: We begin by establishing the following important Pythagorean KL-distance identity, which we will refer to again later in the paper:
for joint distributions ![]() and
and ![]() . From the
definition of KL-distance and the observation that
. From the
definition of KL-distance and the observation that
![]() , the left side of this equality
becomes:
, the left side of this equality
becomes:
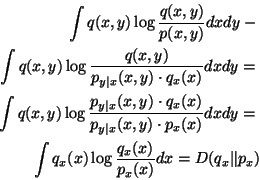
Since by assumption ![]() we may then write:
we may then write:
which is clearly minimized by choosing ![]() to be
to be
![]() ,
i.e.
,
i.e. ![]() , since KL-distance is zero when
its two arguments are the same distribution.
, since KL-distance is zero when
its two arguments are the same distribution.
![]()
Now ![]() is defined in Eq-1 for product
spaces
is defined in Eq-1 for product
spaces ![]() . But the definition easily extends to
more general finite product spaces
. But the definition easily extends to
more general finite product spaces
![]() by letting
by letting ![]() stand for some subset of the
dimensions
stand for some subset of the
dimensions ![]() , and
, and ![]() stand for the others.
The function
stand for the others.
The function ![]() is then defined on the product space
corresponding to the members of
is then defined on the product space
corresponding to the members of ![]() .
.
More formally, let
![]() be a subset of the
dimensions
be a subset of the
dimensions ![]() and
and ![]() be a function of
be a function of
![]() .
Then the operator
.
Then the operator ![]() transforms
transforms ![]() into a new
function whose
into a new
function whose ![]() -marginal exactly matches
-marginal exactly matches
![]() .
.
We view the pair ![]() as a constraint on the behavior of a
desired distribution. Then given a starting distribution
as a constraint on the behavior of a
desired distribution. Then given a starting distribution ![]() ,
and a collection
,
and a collection ![]() ,
, ![]() ,
, ![]() ,
,
![]() of such constraints, a natural approach to the
transformation of
of such constraints, a natural approach to the
transformation of ![]() into a distribution that satisfies all
of them, is to iteratively apply the
into a distribution that satisfies all
of them, is to iteratively apply the ![]() operator -- cycling
through the collection of constraints. One cycle corresponds
to the composition:
operator -- cycling
through the collection of constraints. One cycle corresponds
to the composition:
and many such cycles may be needed.
We remark that in a particular discrete probability setting
this iteration corresponds to Sinkhorn balancing
[23,24]. That is, where
![]() ,
,
![]() ,
, ![]() , and
, and ![]() .
The distribution is then represented by an
.
The distribution is then represented by an ![]() matrix
with nonnegative entries and the iteration corresponds to an
alternating row-wise and column-wise renormalization
procedure. In Sinkhorn's original paper
matrix
with nonnegative entries and the iteration corresponds to an
alternating row-wise and column-wise renormalization
procedure. In Sinkhorn's original paper ![]() and
and ![]() are
uniform and simply scale down the entire matrix so that the
sum of its entries is unity. There is a considerable
literature on this subject, but it is not the focus of our
paper.
are
uniform and simply scale down the entire matrix so that the
sum of its entries is unity. There is a considerable
literature on this subject, but it is not the focus of our
paper.
In the Sinkhorn case, the iteration of Eq-3 gives rise to a constructive algorithm because the simple discrete distributions involved have the property that:
Normal densities represent another important class for which these
properties hold and here too the approach of Eq-3 leads to
a simple and concrete algorithm.
Consider the zero-mean normal distribution on
![]() :
:
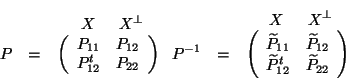
Now for any ![]() consider normal density
consider normal density ![]() on
on
![]() corresponding
to subspace
corresponding
to subspace ![]() . The marginal of
. The marginal of ![]() corresponding to subspace
corresponding to subspace ![]() is
is ![]() . So
. So
![]() .
Ignoring the leading constant and the
.
Ignoring the leading constant and the ![]() term in the exponent
the normal density corresponding to
term in the exponent
the normal density corresponding to ![]() may be written:
may be written:
from which it is clear that
![]() where
where
and for brevity in what follows we abuse our ![]() notation and write:
notation and write:
It is important to notice that this operation is best carried
out using the inverses of the matrices involved. That is,
given ![]() one arrives at
one arrives at ![]() by simply adding
by simply adding
![]() to its upper left block.
to its upper left block.
The next proposition connects our probabilistic development
involving normal densities, with the simpler notion of
positive definite matrices and their determinants. It
establishes that the Bregman distance [5, equation
1.4] arising from the determinant functional
operating on positive definite matrices ![]() , is
essentially the same as the Kullback-Leibler distance between
the zero-mean normal densities arising from these matrices.
, is
essentially the same as the Kullback-Leibler distance between
the zero-mean normal densities arising from these matrices.
then
![]() , and
, and ![]() is a strictly convex function.
is a strictly convex function.
proof: It is well known that
![]() .
It is also well known that
.
It is also well known that
![]() . Next
recall that the (Frobenius) inner product of two symmetric matrices is
just the trace of their product [14]. So
. Next
recall that the (Frobenius) inner product of two symmetric matrices is
just the trace of their product [14]. So
![]() , whence
, whence
![]() .
Now from our knowledge of normal densities and KL-distance we have that
.
Now from our knowledge of normal densities and KL-distance we have that
![]() is nonnegative, and positive iff
is nonnegative, and positive iff ![]() --
from which it follows that
--
from which it follows that ![]() is positive except when
its arguments are equal.
Since
is positive except when
its arguments are equal.
Since ![]() is continuous and differentiable its strict
convexity is established, i.e., the function's graph lies strictly
to one side of a tangent plane.
We remark that convexity may also be proven by expressing
is continuous and differentiable its strict
convexity is established, i.e., the function's graph lies strictly
to one side of a tangent plane.
We remark that convexity may also be proven by expressing
![]() in the basis where
in the basis where ![]() is
diagonal, noticing that all eigenvalues must be real and
positive, and using the inequality
is
diagonal, noticing that all eigenvalues must be real and
positive, and using the inequality
![]() .
.
![]()
In this light, our iterative approach is seen to be a Bregman
projection method. That is, proposition 1 shows that
the ![]() operator minimizes KL distance between normal
densities, but this is the same as projection under Bregman
distance operating on positive definite matrices using the
determinant functional.
operator minimizes KL distance between normal
densities, but this is the same as projection under Bregman
distance operating on positive definite matrices using the
determinant functional.
So applying the operator ![]() to a matrix
to a matrix ![]() gives
the matrix
gives
the matrix ![]() that is the closest to
that is the closest to ![]() while agreeing
with
while agreeing
with ![]() on subspace
on subspace ![]() .
Given this observation,
the natural algorithm for discovering a matrix that satisfies a
system of such constraints, is to cycle over them using the
.
Given this observation,
the natural algorithm for discovering a matrix that satisfies a
system of such constraints, is to cycle over them using the
![]() operator to forcibly impose each constraint in turn.
operator to forcibly impose each constraint in turn.
Our first theorem states that this natural algorithm works provided that a solution exists, and that it discovers the closest solution to the initial matrix chosen. Its proof requires the following observation which establishes that all members of a bounded Bregman neighborhood are themselves bounded above, and bounded strictly away from zero below.
proof: From the definition of Bregman distance we write
![]() . We are free to choose a basis in which
. We are free to choose a basis in which ![]() is
diagonal since
is
diagonal since ![]() is easily seen to be
basis-invariant. This follows from direct
calculation, or, more interestingly by reasoning that
Bregman distance is essentially the same as KL
distance, which is an entropic property of two normal
densities that fairly clearly coordinate system independent.
Then
is easily seen to be
basis-invariant. This follows from direct
calculation, or, more interestingly by reasoning that
Bregman distance is essentially the same as KL
distance, which is an entropic property of two normal
densities that fairly clearly coordinate system independent.
Then
![]() where
where
![]() denotes
the largest eigenvalue of
denotes
the largest eigenvalue of ![]() , and
, and ![]() is a constant
depending on
is a constant
depending on ![]() . So
. So
![]() as
as
![]() .
Next let
.
Next let ![]() denote the smallest diagonal element of
denote the smallest diagonal element of ![]() .
Then
.
Then
![]() .
Here
.
Here
![]() as
as
![]() , whence elements of any
bounded Bregman neighborhood must have spectra
bounded above, and bounded strictly away from zero below
, whence elements of any
bounded Bregman neighborhood must have spectra
bounded above, and bounded strictly away from zero below
![]()
proof: We write the cyclic iteration as:
![\begin{eqnarray*}
P_1 & = & S_{X_0,Q_0}(P_0) \\
\vdots & & \vdots \\
P_{n+1} & = & S_{X_{[n]_m},Q_{[n]_m}}(P_n)
\end{eqnarray*}](img146.gif)
Then for any positive definite matrix
![]() such that
such that
![]() ,
,
![]() , we have from equation 2
that:
, we have from equation 2
that:
![\begin{eqnarray*}
\scriptstyle 0 \leq D(P_1,D) & \scriptstyle = & \scriptstyle ...
...tstyle D(P_n,D) - D([P_n]_{X_{[n]_m},X_{[n]_m}}, Q_{[n]_m}) \\
\end{eqnarray*}](img149.gif)
It is then clear that
![]() , for all
, for all ![]() , and that:
, and that:
![\begin{displaymath}
\sum_{n = 0}^\infty D([P_n]_{X_{[n]_m},X_{[n]_m}},
Q_{[n]_m}) < \infty
\end{displaymath}](img152.gif)
Now the set ![]() of iterates has bounded Bregman
distance to
of iterates has bounded Bregman
distance to ![]() , so by proposition 3 this
set is bounded. Therefore a concentration point
must exist. Since
, so by proposition 3 this
set is bounded. Therefore a concentration point
must exist. Since ![]() is bounded
strictly away from zero, its closure, and therefore
all concentration points must be positive definite.
is bounded
strictly away from zero, its closure, and therefore
all concentration points must be positive definite.
Next observe that any concentration point must be stationary
under ![]() since this is a continuous mapping (in
since this is a continuous mapping (in ![]() ).
It then follows that there is a unique concentration point
which we denote by
).
It then follows that there is a unique concentration point
which we denote by ![]() . Moreover, its stationarity implies
that it satisfies all constraints.
. Moreover, its stationarity implies
that it satisfies all constraints.
Now it is easy to see that:
![\begin{displaymath}
B(\bar{P}, D) = B(P_0, D) - \sum_{n=0}^\infty
B([P_n]_{X_{[n]_m},X_{[n]_m}}, Q_{[n]_m})
\end{displaymath}](img154.gif)
Letting ![]() this implies that
this implies that
![]() . But then
. But then
![]()
![]()
We remark that a similar theorem and proof exist for alternatives to cyclic iteration such as the greedy approach in which a subspace having maximal distance to the target distribution is selected at each iteration.
In the Bregman framework, the constraint set corresponds to an intersection of convex subspaces, and the iteration converges to the point in this intersection closest to the starting point. Elements of the intersection (matrices satisfying all constraints) are stationary under the iteration.
A lot more can be said about the iteration of theorem 1. Later we discuss its rate of convergence, describe cases for which it converges in a finite number of iterations, prove that similar results hold for alternatives to the cyclic constraint ordering, and give a setting under which its computation is particularly fast.
When the intersection consists of more than one point Bregman observes that his iterative projection framework can do more than discover an arbitrary one -- it can be guided, through appropriate selection of an initial value, to converge on the point that solves some minimization problem over the intersection region. In our case it can maximize the determinant, and we will show later that the our algorithm may be used to rapidly compute the maximum determinant positive definite completion of a band matrix.
But our next step is to directly connect theorem 1 to
certain problems of semidefinite programming. See [12,11]
for a review and connections to combinatorial optimization.
In what follows we denote Frobenius matrix inner product by ![]() .
The semidefinite programming problem we address is:
.
The semidefinite programming problem we address is:
Given, find a matrix
that minimizes
, subject to
and
,
.
and we will refer to it as CLS-SDP, standing for constrained linear subspace semidefinite programming. We observe that the semidefinite relaxation of MAX CUT given in [11] is an instance of CLS-SDP. The following proposition connects the distance minimization goal of theorem 1 to this problem.
proof: Given ![]() , we have from Eq
6:
, we have from Eq
6:
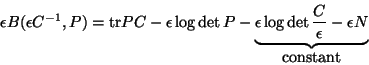
As
![]() the role of
the role of ![]() diminishes and the focus is increasingly on
diminishes and the focus is increasingly on ![]() , or
, or ![]() . We remark that when the constraints correspond to
central minors of a single band matrix, starting points of the
form
. We remark that when the constraints correspond to
central minors of a single band matrix, starting points of the
form
![]() can be shown to
function in the same way where
can be shown to
function in the same way where ![]() is any nonnegative diagonal
matrix.
is any nonnegative diagonal
matrix.
Now given ![]() denote by
denote by ![]() the
unique solution to the minimization of
the
unique solution to the minimization of
![]() . Next let
. Next let ![]() denote the minimum value of
denote the minimum value of
![]() achieved for an instance of CLS-SDP.
It is easy to see that if
achieved for an instance of CLS-SDP.
It is easy to see that if
![]() then
then
![]() .
That
.
That ![]() may be viewed as an approximate solution to the original
problem is established by proposition 6, but
we first establish a technical result needed for its proof.
may be viewed as an approximate solution to the original
problem is established by proposition 6, but
we first establish a technical result needed for its proof.
proof: We will bound
![]() , the largest
eigenvalue of
, the largest
eigenvalue of ![]() . Choose some
. Choose some
![]() satisfying the constraints. Then
satisfying the constraints. Then
![]() establishing an upper bound on
establishing an upper bound on
![]() independent of
independent of ![]() .
.
For any unit length vector ![]() it is easy to show that
it is easy to show that
![]() , the smallest eigenvalue of
, the smallest eigenvalue of ![]() .
It follows that
.
It follows that
![]() provides a lower bound
on the diagonal elements of
provides a lower bound
on the diagonal elements of ![]() that holds
for any basis in which
that holds
for any basis in which ![]() is expressed. So choosing
a basis that diagonalizes
is expressed. So choosing
a basis that diagonalizes ![]() we have that
we have that
![]() .
It also follows that
.
It also follows that
![]() . Combining these we establish
the lower bound
. Combining these we establish
the lower bound
![]() .
Eventually, as increasing
.
Eventually, as increasing
![]() are
postulated, the lower bound exceeds the upper bound --
establishing an upper bound on
are
postulated, the lower bound exceeds the upper bound --
establishing an upper bound on
![]() independent of
independent of ![]() .
.
![]()
proof: Select some
![]() satisfying the constraints
and choose
satisfying the constraints
and choose ![]() such that
such that
![]() . Next let
. Next let ![]() denote a solution to the
CLS-SDP instance. That is, a matrix that satisfies
the constraints such that
denote a solution to the
CLS-SDP instance. That is, a matrix that satisfies
the constraints such that ![]() achieves its
minimal value
achieves its
minimal value ![]() . Define
. Define
![]() . Notice
. Notice
![]() satisfies the constraints, that
satisfies the constraints, that
![]() provided
provided ![]() , and
that
, and
that
![]() . Now:
. Now:
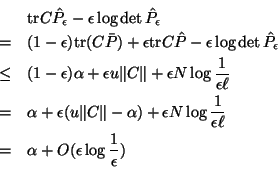
Now by definition
![]() . From proposition
5 we have that
. From proposition
5 we have that
![]() so
so
![]()
![]()
The ``band matrix'' setting provides
an elegant application of proposition
4 and theorem 1. That is, ![]() matrices with nonzero entries confined to distance
matrices with nonzero entries confined to distance ![]() from the
diagonal. Propositions 8 gives
a key result for this setting and the following general
observation is key to both of them. It tells us that when a
marginal constraint that straddles the two components of
a product distribution is forced by applying
from the
diagonal. Propositions 8 gives
a key result for this setting and the following general
observation is key to both of them. It tells us that when a
marginal constraint that straddles the two components of
a product distribution is forced by applying ![]() , then the
result exhibits marginals that agree with the component
distributions provided that the constraint agrees with a given
component on the region of overlap.
, then the
result exhibits marginals that agree with the component
distributions provided that the constraint agrees with a given
component on the region of overlap.
proof: We write:
To evaluate its ![]() marginal we first integrate over
marginal we first integrate over ![]() yielding
yielding ![]()
![]() , and then integrate
over
, and then integrate
over ![]() giving
giving
![]() . Now
if
. Now
if
![]() then the result is
then the result is ![]() as
desired. The same argument applies to the
as
desired. The same argument applies to the ![]() marginal
case.
marginal
case.
![]()
Our first band-matrix result applies the development above to solve the ``band matrix completion problem.'' [13]. It is fascinating that we can reason about this rather pure matrix problem and so easily solve it using a probabalistic outlook and the language of normal densities.
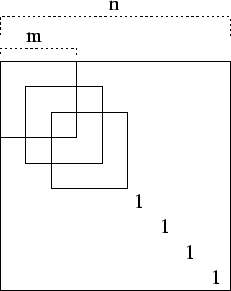
proof: We first argue that the process terminates in ![]() steps.
The sequence of computation is
depicted in figure 1. Notice that since the starting matrix is
diagonal, and each application of
steps.
The sequence of computation is
depicted in figure 1. Notice that since the starting matrix is
diagonal, and each application of ![]() only affects a central minor,
the final result must also have band structure.
By definition
the first application of
only affects a central minor,
the final result must also have band structure.
By definition
the first application of ![]() enforces the constraint corresponding
the the first central minor of
enforces the constraint corresponding
the the first central minor of ![]() .
.
After ![]() applications we consider the space to be a product of
two subspaces. The first corresponding to
diagonal elements
applications we consider the space to be a product of
two subspaces. The first corresponding to
diagonal elements
![]() , and the second to elements
, and the second to elements
![]() . Since the later portion of the matrix is diagonal,
it corresponds to the product of unit variance independent normal
densities, and the product-form requirement of proposition
7 is satisfied.
. Since the later portion of the matrix is diagonal,
it corresponds to the product of unit variance independent normal
densities, and the product-form requirement of proposition
7 is satisfied.
The constraint corresponding to the following application (![]() ) of
) of ![]() is consistent with the constraints enforced earlier because the overlap
of its corresponding central minor of
is consistent with the constraints enforced earlier because the overlap
of its corresponding central minor of ![]() with the
with the
![]() subspace
is a submatrix of the central minors already enforced. Thus, the
subspace
is a submatrix of the central minors already enforced. Thus, the
![]() of the proposition is satisfied. It then follows
that application
of the proposition is satisfied. It then follows
that application ![]() will not disturb the marginals already
enforced -- so after
will not disturb the marginals already
enforced -- so after ![]() applications all constraints are
satisfied and we denote the result
applications all constraints are
satisfied and we denote the result ![]() .
.
Now by theorem 1 ![]() minimizes the
Bregman distance
minimizes the
Bregman distance
![]() subject
to the constraints given by the central minors of
subject
to the constraints given by the central minors of ![]() .
But the diagonal of any
.
But the diagonal of any ![]() satisfying them must match
the diagonal of
satisfying them must match
the diagonal of ![]() , so the
, so the ![]() term is
constant in the minimization, whence
term is
constant in the minimization, whence ![]() maximizes
maximizes ![]() .
. ![]()
 |
A naive implementation of the computation of proposition
8 requires ![]() time. But if
time. But if ![]() is an
is an
![]()
![]() -band matrix, recall that the linear system
-band matrix, recall that the linear system
![]() can be solved in
can be solved in ![]() operations. If
operations. If ![]() is
nonsingular, its inverse can then be constructed column by
column, and any constant-sized sub-block is obtained in
is
nonsingular, its inverse can then be constructed column by
column, and any constant-sized sub-block is obtained in ![]() time. So regarding
time. So regarding ![]() as fixed, it is then clear that the
computation of proposition 8 is reduced to
as fixed, it is then clear that the
computation of proposition 8 is reduced to
![]() time. That is,
time. That is, ![]() (the inverse of the
maximum-determinant completion) may be found in
(the inverse of the
maximum-determinant completion) may be found in ![]() time.
Since
time.
Since ![]() is band-structured, it may be inverted in
is band-structured, it may be inverted in
![]() time to yield
time to yield ![]() , so that the entire problem
has this complexity.
, so that the entire problem
has this complexity.
The concrete example above builds intuition, but by instead
framing the problem in more abstract terms we are quickly
led to an ![]() time highly general solution.
time highly general solution.
Given marginals
![]() on
on
![]() , where
we assume without loss of generality that
, where
we assume without loss of generality that ![]() and
and ![]() ,
we can group variables as
,
we can group variables as
![]() where
where
![]() , and so on.
One may think of this as a block tridiagonal representation
of the system of marginals.
, and so on.
One may think of this as a block tridiagonal representation
of the system of marginals.
Starting with any product distribution
![]() we perform the following
Bregman-Sinkhorn iteration:
we perform the following
Bregman-Sinkhorn iteration:
Then the resulting maximum entropy distribution is by induction:
In the Gaussian case we have ![]() where:
where:
Then the maximal determinant completion ![]() has block
tridiagonal inverse structure with diagonal blocks
has block
tridiagonal inverse structure with diagonal blocks
![]() and off-diagonal blocks
and off-diagonal blocks
![]() - where
- where ![]() ,
,
![]() ,
,
![]() .
.
The result may be computed in ![]() time, or only
time, or only
![]() parallel time with
parallel time with ![]() processors.
processors.
The local convergence properties of our positive definite matrix iteration, and those of other instances of deflation-inflation, may be analyzed using the following
![\begin{eqnarray*}
& & \hspace{1.2em} {\mathbb{R}}^n \hspace{0.5em} {\mathbb{R}}...
... \begin{array}{cc}
I & 0 \\ [1ex]
0 & A
\end{array}\right)
\end{eqnarray*}](img248.gif)
where
![]() .
Finally, assume that for some initial point
.
Finally, assume that for some initial point ![]() , the sequence of
iterates defined by
, the sequence of
iterates defined by
![]() converges to
converges to
![]() .
Then the rate of convergence is linear.
.
Then the rate of convergence is linear.
proof: Convergence implies that for sufficiently
large ![]() ,
,
![]() where
where
![]() and
and
![]() and
and
![]() is analytic at
is analytic at ![]() .
Thus
.
Thus
![]() ,
where
,
where
![]() . Observe that the condition
. Observe that the condition
![]() implies
implies
![\begin{displaymath}
J_n =
\left( \begin{array}{cc}
I & B_n \\ [1ex]
0 & A_n
\end{array}\right)
\end{displaymath}](img258.gif)
Corollaries to these lemmas establish linear convergence for our normal-density inspired positive definite case, and provide a concise proof for a rather general form of Sinkhorn balancing. For a general Sinkhorn balancing we prove that the rate of convergence is linear iff the initial zero pattern is equal to the zero pattern of the limit. The statement and proofs of these results will be presented in the full paper.
Beyond local rate of convergence we are interested in a bound on the total number of operations required to produce an approximate solution. Our analysis applies to a form of the algorithm in which the next diagonal position to update is chosen greedily, rather than in a simple cyclic fashion. That is, we update the diagonal element that generates the largest immediate reduction in KL distance. A similar analysis is possible for the somewhat more practical ordering based on KL distance for each marginal, i.e. for each diagonal element.
The analysis requires a number of technical lemmas and is rather involved. We sketch its development here leaving the details for the full paper. The main theorem we establish is:
As the algorithm runs, the diagonal of ![]() approaches
approaches
![]() . It is first shown that the error in diagonal
elements must be no more than
. It is first shown that the error in diagonal
elements must be no more than
![]() to achieve
the desired
to achieve
the desired ![]() approximation. This results
from the observation that it is enough to continue until the
KL distance to the optimal solution is
approximation. This results
from the observation that it is enough to continue until the
KL distance to the optimal solution is ![]() .
.
Next, the initial KL distance is easily shown to be ![]() .
We denote by
.
We denote by ![]() the maximum diagonal error we will accept.
That is, the algorithm will terminate once the maximum
diagonal error less than
the maximum diagonal error we will accept.
That is, the algorithm will terminate once the maximum
diagonal error less than ![]() . Then from proposition
1 it follows that every diagonal update, up until we
stop, must generate at least
. Then from proposition
1 it follows that every diagonal update, up until we
stop, must generate at least ![]() improvement in KL
distance. So
improvement in KL
distance. So
![]() steps are required.
Letting
steps are required.
Letting
![]() we arrive at an easy
we arrive at an easy
![]() naive bound.
naive bound.
We remark that this naive analysis may be adapted to the Sinkhorn case.
Fortunately, much stronger bounds may be developed for our
normal density setting. The first step consists of letting
![]() and showing that in
and showing that in
![]() steps the solution comes within a unit KL ball.
steps the solution comes within a unit KL ball.
Once within this ball it may be shown that only
![]() steps are required to come within any fixed
power of
steps are required to come within any fixed
power of ![]() distance from the optimal solution - in
particular within
distance from the optimal solution - in
particular within
![]() .
This improves our bound to
.
This improves our bound to
![]() , but additional
improvement is possible.
, but additional
improvement is possible.
The final idea consists of appropriate ![]() scheduling. This improves the first phase of the algorithm
where the objective is to come within unit distance. We
employ a series of shrinking
scheduling. This improves the first phase of the algorithm
where the objective is to come within unit distance. We
employ a series of shrinking ![]() values where each
is a constant factor smaller then the previous one.
This constant is of the form
values where each
is a constant factor smaller then the previous one.
This constant is of the form ![]() ) for some constant
) for some constant ![]() .
For each value
.
For each value ![]() we perform
we perform
![]() diagonal operations
bringing us close enough to
diagonal operations
bringing us close enough to
![]() so that the ultimate
effect is that after
so that the ultimate
effect is that after
![]() steps we
come within unit distance of
steps we
come within unit distance of ![]() as required.
The second phase of the algorithm then runs, completing the solution.
as required.
The second phase of the algorithm then runs, completing the solution.
We remark that while we do not use the interior point method in the typical fashion as a black box, several aspects of our analysis borrow from ideas at the heart of it's analysis. Also, while our development follows an entirely different probabalistic line, it is interesting to note that we arrive at the same barrier function, which appears there.
To give a more detailed view of the technical analysis we state main lemmas here without proof.
As remarked above, essentially the same naive analysis applies to
``greedy'' Sinkhorn balancing. Suppose ![]() is a row-normalized square
incidence matrix of a bipartite graph
is a row-normalized square
incidence matrix of a bipartite graph ![]() .
.
On each step of our algorithm in its greedy form we choose
that row or column having sum of elements ![]() such that
such that
![]() is maximal, and divide all entries in it by
is maximal, and divide all entries in it by
![]() .
.
It follows directly from [5] that this algorithm
converges if and only if ![]() has a perfect matching.
has a perfect matching.
Using Hall's theorem it is easy to prove (and well known) that
if at some iteration
![]() then a perfect matching exists.
then a perfect matching exists.
Now suppose that ![]() is any double-stochastic matrix with:
is any double-stochastic matrix with:
then from proposition 1, adapted to this distance, it follows that:
Thus the number of iterations required to reach the condition
![]() is at most
is at most
![]() ,
since
,
since
![]() for all
for all ![]() , where
, where ![]() is some
small universal constant.
is some
small universal constant.
Next, if ![]() is a permutational matrix of a perfect matching for
is a permutational matrix of a perfect matching for
![]() , then
, then
![]() , where
, where
![]() denotes the degree of vertex
denotes the degree of vertex ![]() .
.
We have therefore produced a balancing algorithm that checks
the existence of a perfect matching requiring
![]() time or
time or
![]() parallel steps given
parallel steps given ![]() processors.
Here
processors.
Here ![]() denotes the number of edges in
denotes the number of edges in ![]() .
.
Our Deflation-Inflation approach can not address semidefinite programming problems in general form but we remark that our CLS-SDP variant includes problems that can not be formulated as conventional instances of semidefinite programming without the introduction of a large number of constraints. Namely, instances that involve constraints that are expressed in terms of transformed linear subspaces. We also emphasize that our method is particularly attractive for specially structured matrices, and in particular for band matrices.
In our probabalistic framework we use normal densities, which may be thought of as capturing second-order relationships between vertices - namely edges. We speculate that different probability functions might lead to interesting results. Other members of the exponential family might be considered, or higher-order generalizations of normal densities.
It is clear that any global analysis of projection-based convex optimization methods (such as EM) requires bounds on the relationship between global KL distance and marginal distances. During our analysis we remark that machinery from [21] was borrowed to allow us to establish some bounds of this sort. These entropic inequalities may be of independent interest.
Finally we remark that there is tension between work invested
in generating random cuts, and work aimed at solving the semidefinite
program for ever smaller ![]() values. Another interesting area for
future work is to focus on the variance of
the cuts generated in order to better understand this tradeoff.
values. Another interesting area for
future work is to focus on the variance of
the cuts generated in order to better understand this tradeoff.
This document was generated using the LaTeX2HTML translator Version 2K.1beta (1.47)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -image_type gif -nonext_page_in_navigation -noprevious_page_in_navigation -up_url ../main.html -up_title 'Publication homepage' -accent_images textrm -numbered_footnotes maxg.tex
The translation was initiated by Peter N. Yianilos on 2002-06-25