Andrew V. Goldberg and Peter N. Yianilos
NEC Research Institute, Inc.
4 Independence Way
Princeton, NJ 08540
Andrew V. Goldberg and Peter N. Yianilos
NEC Research Institute, Inc.
4 Independence Way
Princeton, NJ 08540
This paper presents a framework for the design of an Intermemory, and considers certain aspects of the design in greater detail. In particular, the aspects of addressing, space efficiency, and redundant coding are discussed.
Keywords: Archival Storage, Distributed Redundant Databases, Electronic Publishing, Distributed Algorithms, Error Correcting Codes, Erasure-Resilient Codes, Information Dispersal Algorithm, Digital Library, Internet.
Through publication we preserve and transmit our knowledge and culture. Electronic media promises to improve transmission but the important issue of preservation has yet to be addressed in the context of the emerging worldwide network of computers.
Print publications are preserved by our collective agreement to fund and support libraries at educational institutions and several levels of government. This solution amounts to a distributed redundant storage scheme and is further strengthened by its self-organizing nature. That is, there is no essential central world library. It is possible that the role of libraries will simply expand to include the collection of purely electronic items but in this paper we explore another possibility: that a largely self organizing distributed world memory might emerge.
Our first thought was that commercial services might arise to offer archival data storage. In this scenario the publisher of an academic journal might, for example, pay an up-front fee to ensure that a journal issue will be available archivally in electronic form. The data would be widely distributed, and financial reserves established to care for it in the future. Sloan suggests a simpler alternative in [18]; that such a service might be provided by a single major university or other institution. These approaches are, however, inconsistent with the essential spirit of the Internet, i.e. growth and effectiveness in the absence of strong central control or commercial organization.
Given the current state of world connectivity, and the clear prospects for continued growth, widely distributing archival data is not a significant technical problem. Ensuring that it survives is the real issue since unlike books which persist for centuries or more, machines have lifetimes measured in small numbers of years.
In the solution we envision, a user donates storage space ![]() to the
Memory for a period of time, and in return receives the right to
store a much smaller amount of data
to the
Memory for a period of time, and in return receives the right to
store a much smaller amount of data ![]() in it. A three-year donation of one
gigabyte might, for example, correspond to the right to archivally store 200
megabytes. Here the system's efficiency
in it. A three-year donation of one
gigabyte might, for example, correspond to the right to archivally store 200
megabytes. Here the system's efficiency ![]() is
is ![]() .
.
Our approach rests on an assumption of continued system growth. Falling costs per bit of data storage and growth in the number of Internet/Web users and their appetite for data storage are supporting factors. It is because of this assumption that a bounded-time donation of storage space can correspond to an unbounded-time storage space grant. The system's efficiency factor must be low enough to support this trade and to allow sufficiently wide distribution of each memory item.
This paper begins the process of formalizing the notion of Intermemory, presents specific proposals for certain aspects of its design, and comments on the manifold other challenges that must be addressed before the first stable and secure Intermemory goes online.
We remark that large organizations might implement one or more private Intermemories resulting an Intramemory that is maintained without explicit backup over the organization's wide area network. The public Intermemory that motivated this paper is in this sense the world's memory.
The contributions of this paper are:
The growing interest in digital libraries was recently surveyed [17] and a general discussion of the problem of preserving digital documents is contained in [16]. We observe that libraries serve two distinct roles: maintenance of a historical record, and selection of appropriate materials. Web-indexing approaches dispense with the second role and allow a user to view all the world has to offer. They fail, however, to deal with the first. Creating a record of everything on the Internet [9] represents, by contrast, an emphasis on the first role and eliminates entirely the second. Our concept of Intermemory combines the archival function with what amounts to a self-selecting publication process. It is worthwhile noting that Intermemory solves the preservation problem associated with the ephemeral nature of computer storage media. As new subscribers replace old ones, memories are automatically copied onto the latest medium.
Anderson's work [3] parallels our own, but his emphasis is on the freedom-of-expression and individual rights rationale, and less on the specific technical and architectural issues involved.
The problem of efficiently distributing a file within a distributed system having connectivity described by a given undirected graph is considered in [11]. That is, a node can reconstruct data from its neighbors. This idea is related to that of diversity coding (see [15] for recent work) in which there are multiple encoders and each of several decoders has access to some fixed subset of the encoders. By contrast, we assume that the world network provides a complete graph. So while this work is clearly related to our problem it does not appear to be directly relevant.
The topic of [10] is a discussion, in general terms, of several design issues and tradeoffs relating to the implementation of redundant distributed databases. Similar issues are discussed in [1] and both papers cite Rabin's work [14], which introduced the idea of coding-based redundancy to the database community. He in turn recognizes the earlier related work [5]. Odlyzko is also interested in perpetual storage [12], where his focus is on preservation of and access to research literature.
The redundant array of inexpensive disks (RAID) approach [13] distributes a file system over an array of disks directly attached to a host computer. Redundancy is provided by variations of a simple parity approach. Further distributing not only the storage, but also the control of a file system, is the subject of numerous papers including [4], which describes the xFS system now under development. This system distributes a file system over cooperating workstations while retaining high performance. By contrast: i) our proposed Intermemory includes redundancy and dispersal on a much larger scale, and is capable of tolerating the loss of a large portion of the participating nodes, ii) the emphasis is on the archival aspect rather than on performance, iii) participating processors are assumed to be widely dispersed on the world internet, their participation of an ephemeral nature and subject to very little central control, iv) adversarial attacks are a primary Intermemory design concern, v) our focus is on implementing a block-level substrate upon which more than one file system format might be implemented over time, and vi) because of our emphasis on archiving, a write-once model is our starting point with research continuing towards a read-write system.
 |
For the purposes of this paper the Intermemory is an immense,
distributed, self-organizing, persistent RAM containing ![]() memory
blocks. It is addressed by an
memory
blocks. It is addressed by an ![]() -bit binary address, and each
block consists of
-bit binary address, and each
block consists of ![]() words of
words of ![]() bits. Subscribers are allocated
fixed addresses into which only they may write. We assume a write-once
model: once written, the data cannot be modified or deleted.
Anyone may read from any location.
bits. Subscribers are allocated
fixed addresses into which only they may write. We assume a write-once
model: once written, the data cannot be modified or deleted.
Anyone may read from any location.
To achieve wide-spread use the Intermemory will, no doubt, have to deal with many high-level issues such as intelligent addressing, search and perhaps other functions built on top of the simple substrate we consider -- as well as interpretation of specific data types (such as text, image, and even programs) in an archival manner. These topics are beyond the scope of this paper. We also set aside the important cryptographic issues that must ultimately be addressed for the system to honor its archival promise -- and at a low level, enforce write permissions and provide data authentication. Yet other dimensions of the problem are identified in sections 3 and 4.
We contend, however, that while deployment of a complete system in the
senses identified above is a daunting task, less complete solutions
are practical today. To support this contention we have chosen to
present our Intermemory design in rather concrete terms in which
specific values are proposed for the system parameters such as
![]() ,
, ![]() , etc. In order to illuminate the architectural issues
underlying each of these design decisions we will comment on the
tradeoffs that apply.
, etc. In order to illuminate the architectural issues
underlying each of these design decisions we will comment on the
tradeoffs that apply.
A world-wide fully connected network is assumed such that the Intermemory service on each participating processor can be contacted at some network address (NA) - today an IP address and port number suffice.
In this section we describe a particular scheme based on well-known
erasure codes and the idea of using them for information
dispersal.
For simplicity we will assume that the ![]() words within each block are
elements of some finite field
words within each block are
elements of some finite field ![]() of approximately
of approximately ![]() elements.
The natural choice of
elements.
The natural choice of ![]() with prime
with prime
![]() allows for simple computation at the expense of a very small increase
in storage space when translating the original block to field-element
representation. These words may then be regarded as the coefficients
of a polynomial of degree
allows for simple computation at the expense of a very small increase
in storage space when translating the original block to field-element
representation. These words may then be regarded as the coefficients
of a polynomial of degree ![]() over
over ![]() . Then the value assumed by
this polynomial at any
. Then the value assumed by
this polynomial at any ![]() distinct points suffice to uniquely
identify it. This classical observation is a key idea in coding
theory [6] and corresponds to the Vandermonde matrix
case of Rabin's information dispersal framework [14] in the
extreme setting where each block contains a single word. The idea is
that one may evaluate the polynomial at
distinct points suffice to uniquely
identify it. This classical observation is a key idea in coding
theory [6] and corresponds to the Vandermonde matrix
case of Rabin's information dispersal framework [14] in the
extreme setting where each block contains a single word. The idea is
that one may evaluate the polynomial at ![]() points, expanding
the block by a factor of
points, expanding
the block by a factor of ![]() , such that any set of
, such that any set of ![]() values suffices
to reconstruct the original block - with these separate values
dispersed among subscribing processors. Note that we must have
values suffices
to reconstruct the original block - with these separate values
dispersed among subscribing processors. Note that we must have
![]() . The approach is space-optimal since every subset of
processors sufficient for reconstruction, i.e. of size
. The approach is space-optimal since every subset of
processors sufficient for reconstruction, i.e. of size ![]() , contains
exactly the total space of the original data. Encoding and decoding
correspond to the polynomial evaluation and interpolation
problems respectively. Using
, contains
exactly the total space of the original data. Encoding and decoding
correspond to the polynomial evaluation and interpolation
problems respectively. Using ![]() FFT-based polynomial
multiplication one may perform both evaluation [8] and
interpolation in
FFT-based polynomial
multiplication one may perform both evaluation [8] and
interpolation in ![]() time. Since these algorithms are
also efficient in practice, encoding and decoding complexity does not
limit our choice of
time. Since these algorithms are
also efficient in practice, encoding and decoding complexity does not
limit our choice of ![]() . We remark that more complex coding schemes
[2] might be considered that are asymptotically faster yet but
require slightly more than
. We remark that more complex coding schemes
[2] might be considered that are asymptotically faster yet but
require slightly more than ![]() words to reconstruct the original.
Also, the topic of reconstruction given some number of erroneous
values has been considered in the literature.
words to reconstruct the original.
Also, the topic of reconstruction given some number of erroneous
values has been considered in the literature.
The ![]() word output block may be arbitrarily divided into
subblocks and dispersed among subscribing processors. The maximum
dispersal possible using the scheme above sends a single word to each
of
word output block may be arbitrarily divided into
subblocks and dispersed among subscribing processors. The maximum
dispersal possible using the scheme above sends a single word to each
of ![]() processors. An adversary would then have to destroy
processors. An adversary would then have to destroy
![]() processors (
processors (![]() in our example below) to erase a maximally
dispersed memory block. The minimum dispersal consists of storing the
entire output block at one processor. The primary consideration in
establishing
in our example below) to erase a maximally
dispersed memory block. The minimum dispersal consists of storing the
entire output block at one processor. The primary consideration in
establishing ![]() is the tradeoff between the degree of information
dispersal possible, and the inconvenience of large blocks (by today's
standards).
is the tradeoff between the degree of information
dispersal possible, and the inconvenience of large blocks (by today's
standards).
 |
Given ![]() and
and ![]() it follows that
it follows that
![]() minimizes the input data block size which is then
minimizes the input data block size which is then
![]() bits. For example,
bits. For example, ![]() and
and ![]() gives
gives ![]() and a block size of 64 kilobytes.
If
and a block size of 64 kilobytes.
If ![]() is used then the requirement
is used then the requirement
![]() forces
forces ![]() to be slightly less than
to be slightly less than ![]() .
.
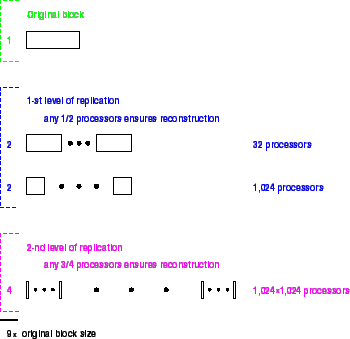
Reading a maximally dispersed block is a very expensive operation in any model in which network connections have significant cost. For this reason we propose that each data block be stored at several levels of dispersal. In the example above, the encoded block might be stored:
In most cases we expect the block to be readable by contacting a single
processor. If this fails we must contact at least 16 of the 32 at the
next level, and so on. The interesting property of the encoding
transformation is that this dispersal takes place with no additional
computation. That is, blocks are merely subdivided and dispersed. To
read a block, it is merely necessary that a sufficient number of words
from the encoded block can be accessed. These might come from
different levels. These four levels consume ![]() the storage of
the original block (not
the storage of
the original block (not ![]() because the first level need not include
any redundancy at all). The idea, then, is that space is traded for reduced
expected read time.
because the first level need not include
any redundancy at all). The idea, then, is that space is traded for reduced
expected read time.
As fragments of a block are received at a processor, they are stored in its memory along with the corresponding address and index within the block. Separate storage areas exist for the different fragment lengths corresponding to the four levels of dispersal above.
Because block addresses must be stored along with each fragment1, maximal
dispersal introduces large space penalties, on the assumption that ![]() .
For this reason we suggest that the bottommost level be omitted.
The new bottommost level disperses to
.
For this reason we suggest that the bottommost level be omitted.
The new bottommost level disperses to ![]() processors.
processors.
A second phase of dispersal is then possible in which the contents of
the bottom level incoming data buffer is treated as a data block and
further dispersed. This dispersal does not take place until the this
buffer has accumulated a full block. We suggest a single wide-spread
![]() dispersal to, say, another
dispersal to, say, another ![]() processors. In this way the
processor's bottom-level buffer is, in effect, backed up in the
network. The result is that an adversary must attack
processors. In this way the
processor's bottom-level buffer is, in effect, backed up in the
network. The result is that an adversary must attack
![]() processors (
processors (![]() of the
of the ![]() involved) to erase a memory block
that has been dispersed to this degree (assuming there enough
processors in the network to allow such dispersal). Notice that
replacing the bottom level with a second phase of dispersal increases
the overall space cost to
involved) to erase a memory block
that has been dispersed to this degree (assuming there enough
processors in the network to allow such dispersal). Notice that
replacing the bottom level with a second phase of dispersal increases
the overall space cost to ![]() because of the additional
redundancy introduced by the second phase.
Multilevel dispersal schemes such as
this represent an effective way to limit the overhead of address
storage while achieving very wide dispersal and moderate block size.
because of the additional
redundancy introduced by the second phase.
Multilevel dispersal schemes such as
this represent an effective way to limit the overhead of address
storage while achieving very wide dispersal and moderate block size.
In the system we propose a failed processor is detected by its neighbors, its data reconstructed, and its storage responsibilities assumed by another processor in the network. The manner in which these failures are detected and the reconstruction accomplished is discussed later.
Dispersal on the scale proposed above is not necessary to achieve archival performance under a model in which network or processor failures are assumed to be independent. But an assumption of independence is far from valid for many reasons. These include systematic failures introduced by software bugs, viruses, and overt adversarial action. We suggest that a healthy Intermemory might result from many independent implementations of the distributed algorithm starting from a common specification that is simple enough to be formally verified.
The probability of losing even one memory block is then dominated by the
probability that one will, despite the repair activities mentioned above,
permanently lose access to
![]() processors,
spread randomly (by virtue of the addressing approach described later)
throughout the network. We will not present calculations here because
the issue of an appropriate failure model is beyond the scope of this paper.
But it clear that the degree of maximum dispersal is the key variable.
processors,
spread randomly (by virtue of the addressing approach described later)
throughout the network. We will not present calculations here because
the issue of an appropriate failure model is beyond the scope of this paper.
But it clear that the degree of maximum dispersal is the key variable.
The discussion above illustrates how the variables ![]() ,
, ![]() ,
, ![]() ,
,
![]() , and the choice of levels and phases of distribution are related
in the design of an efficient Intermemory, and we next turn to the
system's behavior over time.
, and the choice of levels and phases of distribution are related
in the design of an efficient Intermemory, and we next turn to the
system's behavior over time.
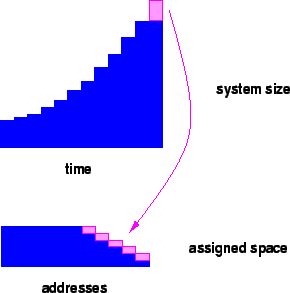 |
In our model of Intermemory, each subscriber ``invests'' a certain amount of memory for a certain time period and earns ``interest'' at each time unit. Then the original investment is withdrawn but the interest remains invested and represents the user's perpetual ownership of space within the system. Subscribers enter the system and later leave it but we assume that the net effect is that total investment increases over time. The source of the ``interest'' is the system's assumed continued expansion. That is, each unit of growth in the system's total capacity is paid-out as ``interest'' to current and in some cases to past subscribers.
More precisely,
we measure participation in the system in terms of an
arbitrary unit of memory. The number of units participating
at time ![]() is denoted
is denoted ![]() . Time is discretized and we
model the system's growth over time as:
. Time is discretized and we
model the system's growth over time as:
The rate ![]() is the reciprocal of each processor's expected
lifetime, and
is the reciprocal of each processor's expected
lifetime, and ![]() combines the effects of new users joining
the system, and technology improvements making it possible for
new entrants to contribute an increasing amount of space. We
assume
combines the effects of new users joining
the system, and technology improvements making it possible for
new entrants to contribute an increasing amount of space. We
assume ![]() . Then the growth in space from time
. Then the growth in space from time ![]() to
time
to
time ![]() is
is
We allow each unit to consume this space storing its memories into the Intermemory. So over each unit's expected lifetime it may spend:
This expression makes clear that longer lived processors directly compensate for a lower growth rate. Today storage costs are declining rapidly and computers are frequently discarded or redeployed after only a few years use. If one expects costs to fall slower in the future then constant efficiency can be maintained to the extent that processors stay on the job for a longer time. But it is certainly possible that the system's efficiency would decline over time making it less attractive to new subscribers.
Example: Suppose ![]() is measured in days and we expect
processors to participate for
is measured in days and we expect
processors to participate for ![]() days so
days so ![]() .
Next suppose
.
Next suppose ![]() . Notice that
. Notice that
![]() so that we are assuming an annual
system growth rate of roughly
so that we are assuming an annual
system growth rate of roughly ![]() . Now
. Now ![]() so
so
![]() and over its 1000 day lifetime a
processor will accrue the right to consume roughly
and over its 1000 day lifetime a
processor will accrue the right to consume roughly ![]() units
of perpetual storage space. So in this example, selected to
be plausible, each participating processor can consume half of
the memory it donates. An actual system will have to confront
the possibility that the combination of growth rate and death
rate falls short of expectations, and somehow regulate the
consumption of new memory.
units
of perpetual storage space. So in this example, selected to
be plausible, each participating processor can consume half of
the memory it donates. An actual system will have to confront
the possibility that the combination of growth rate and death
rate falls short of expectations, and somehow regulate the
consumption of new memory.
In the development above, new space entering the system is
allocated to the system's current subscribers, i.e. at time
![]() . So a subscriber's rights vest only during its life.
We now explore the effect of a different strategy where
the allocation is made to subscribers at time
. So a subscriber's rights vest only during its life.
We now explore the effect of a different strategy where
the allocation is made to subscribers at time ![]() .
Over a unit's expected lifetime it may then spend:
.
Over a unit's expected lifetime it may then spend:
As
![]() it seems that a
processor may enjoy an unbounded right to consume space -
and indeed this is true. But such a system is not practical
because it does not represent a fair trade. The subscriber,
clearly, expects to vest some rights within a reasonable
period of time. It nevertheless serves to illustrate that
delayed vesting can boost system efficiency.
it seems that a
processor may enjoy an unbounded right to consume space -
and indeed this is true. But such a system is not practical
because it does not represent a fair trade. The subscriber,
clearly, expects to vest some rights within a reasonable
period of time. It nevertheless serves to illustrate that
delayed vesting can boost system efficiency.
In a mixed allocation strategy where a proportion ![]() of the
new space is dispersed with delay
of the
new space is dispersed with delay ![]() a unit may spend:
a unit may spend:
where
![]() and each
and each
![]() .
We remark that uniform allocation over the previous
.
We remark that uniform allocation over the previous ![]() time units
results in a particularly simple expression
time units
results in a particularly simple expression
![]() for a subscriber's ultimate vested space rights.
for a subscriber's ultimate vested space rights.
Example: Under the assumptions of the previous example,
suppose ![]() of the new space is allocated during a
processor lifetime so that the first two levels of dispersal
can occur. Then
of the new space is allocated during a
processor lifetime so that the first two levels of dispersal
can occur. Then ![]() vest during an equally long period
following its death, and the final
vest during an equally long period
following its death, and the final ![]() in a period of the
same length that follows. Here
in a period of the
same length that follows. Here
![]() , and
, and
![]() .
The result is that the processor will eventually accrue the
right to consume
.
The result is that the processor will eventually accrue the
right to consume ![]() units of space - just as much as it
invested.
units of space - just as much as it
invested.
Thus dispersal takes place over time and old memories are dispersed more widely than new ones.
The discussion above is rather simplistic in that it assumes that the system's size grows consistently, and that this growth is governed by a simple exponential rule. A real system will have to confront problems such as:
These problems make clear that some regulation of the vesting of rights is needed in a functioning Intermemory. This is itself an interesting question but is beyond the scope of our paper.
Finally, we observe that one might also assume that the memory capacity of an individual subscriber increases over time. In addition to the effect of declining storage cost, the trend towards more online data per user supports it. Under the addressing method described in the next section this assumption simplifies the handling of buffer overflow in a subscribing processor.
In this section we present a particular scheme for Intermemory addressing. The central design objective is that the important functions of dispersal and self-repair may be performed such that each processor communicates with only a limited number of neighbors, and that the total volume of communication is minimized. Other solutions are possible and our current research is now exploring several variations.
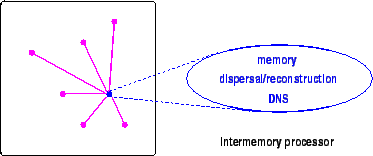
The approach we present here combines hashing, pseudo-random generators, and a distributed name server (DNS). We will not comment on the DNS implementation except to discuss its reconstruction in the event of failure, or replacement. All hash functions and generators are assumed to be publicly known but we will not consider the choice of specific functions.
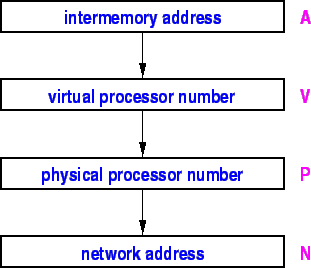
An ![]() -bit Intermemory address
-bit Intermemory address ![]() is first mapped to a
is first mapped to a ![]() -bit
virtual processor number
-bit
virtual processor number ![]() -- where it is assumed that
-- where it is assumed that ![]() exceeds
the number of processors in the network (now or in the future). We
suggest that
exceeds
the number of processors in the network (now or in the future). We
suggest that ![]() and
and ![]() represent reasonable values.
represent reasonable values.
The DNS implements a many-to-one relation between virtual processor numbers, and
physical processor numbers, denoted ![]() . It also implements a one-to-one
relation between physical processor numbers and network addresses, denoted
. It also implements a one-to-one
relation between physical processor numbers and network addresses, denoted ![]() ,
that today would consist of a combined Internet address and port number.
The path is then
,
that today would consist of a combined Internet address and port number.
The path is then
![]() .
.
In this way we locate the actual processor containing the top-level dispersal of a memory block, i.e. the block in its entirety.
A ![]() relation, once established, persists forever - at
least for the purposes of this paper. But the
relation, once established, persists forever - at
least for the purposes of this paper. But the ![]() relation is fluid as processors, and even world-wide network
structure, change. The DNS also accepts responsibility for creating
relations as necessary, and thus serves as a load balancer by
assigning
relation is fluid as processors, and even world-wide network
structure, change. The DNS also accepts responsibility for creating
relations as necessary, and thus serves as a load balancer by
assigning ![]() values used for the first time to lightly loaded
physical processors. Other load balancing operations are possible but
we will not discuss this issue further.
values used for the first time to lightly loaded
physical processors. Other load balancing operations are possible but
we will not discuss this issue further.
 |
A graph relating the processors is defined by using ![]() -values and a
pseudo-random generator, or a family of hash functions. The virtual
numbers of the neighbors of each processor are obtained by seeding
the generator with its physical number
-values and a
pseudo-random generator, or a family of hash functions. The virtual
numbers of the neighbors of each processor are obtained by seeding
the generator with its physical number ![]() , and generating some
number
, and generating some
number ![]() of values - where
of values - where ![]() is no smaller than the maximum
fan-out in the dispersal scheme. Actually, we require
is no smaller than the maximum
fan-out in the dispersal scheme. Actually, we require ![]() distinct neighbors, so more than
distinct neighbors, so more than ![]() pseudo-random values may be
necessary. Notice that this graph is purely a function of the
pseudo-random values may be
necessary. Notice that this graph is purely a function of the ![]() and
the information in the DNS's first relation.
and
the information in the DNS's first relation.
Each processor retains its ![]() value, along with the current
value, along with the current ![]() values corresponding to each neighbor. On DNS failure, we then have a
high-degree random graph interconnecting all subscribers that may be
used for reconstruction. Even if some portion of the network
addresses are nonfunctional, we can with very high probability reach
all processors.
values corresponding to each neighbor. On DNS failure, we then have a
high-degree random graph interconnecting all subscribers that may be
used for reconstruction. Even if some portion of the network
addresses are nonfunctional, we can with very high probability reach
all processors.
We remark that the same network might be used to implement the DNS itself, and its operation might be distributed and performed by a single Intermemory code.
The primary purpose of the graph is information dispersal. Given ![]() ,
,
![]() , and the level of dispersal as seed, another pseudo-random
generator (or collection of hash functions) is used to identify a
subset of the processor's neighbors to which the dispersal takes
place. Thus all processors in a block's distribution tree can be
computed based on
, and the level of dispersal as seed, another pseudo-random
generator (or collection of hash functions) is used to identify a
subset of the processor's neighbors to which the dispersal takes
place. Thus all processors in a block's distribution tree can be
computed based on ![]() and the DNS.
and the DNS.
Another purpose of the graph is repair, and we will sketch this process. Periodic polling of neighbors is used to identify dead processors, and when the processor is replaced this graph is used to reconstruct its proper contents. An item the processor should contain that is not at the top dispersal level must have arrived from another processor. That other processor will eventually poll, notice the item it earlier dispersed is gone, and send it again. A top level item will have been dispersed to at least one level, so the neighbors can be examined for any level two blocks that must, based on the address calculation process above, have arrived from the processor being reconstructed. The corresponding Intermemory addresses are then read and retained. This polling cycle might span, say, a few months. So over that time any new replacement is rebuilt. In an analysis of a complete system the frequency of polling is a key design variable.
We briefly observe that the size of the first DNS relation is ![]() which is approximately
the number of memory blocks in the system plus
which is approximately
the number of memory blocks in the system plus ![]() times the number of subscribing
processors. The size of the second table is just the number of subscribing
processors.
times the number of subscribing
processors. The size of the second table is just the number of subscribing
processors.
We remark that our mapping of an Intermemory address to a virtual
processor number is primarily for semantic reasons. One might, for
example, set ![]() and use the identity hash so that
and use the identity hash so that ![]() . The
semantic distinction is necessary since
. The
semantic distinction is necessary since ![]() refers to the address of
an Intermemory block as communicated by a user to the system, while
refers to the address of
an Intermemory block as communicated by a user to the system, while
![]() is another name for some physical processor. Confusion arises
when
is another name for some physical processor. Confusion arises
when ![]() values are generated as part of graph construction - these
are not Intermemory addresses. Also, a case for large
values are generated as part of graph construction - these
are not Intermemory addresses. Also, a case for large ![]() might be
made based on some decomposition of the address space, while
might be
made based on some decomposition of the address space, while ![]() can
remain small, saving storage space and time in the DNS implementation.
can
remain small, saving storage space and time in the DNS implementation.
Finally we observe that the DNS can be rebuilt entirely from the information held by each subscribing processor. This is performed as a distributed algorithm on the current graph connecting all subscribers. Thus the DNS need not itself be engineered as an archival system, and might even be replaced from time to time.
The problem of buffer overflow must be considered. That is, when a
processor is sent more data than it has room to store. A solution
idea is to design the DNS such that if a processor nears capacity the
likelihood that the DNS assigns a new ![]() to it tends to be small
provided that other processors have more room available. Another
problem arises when a
to it tends to be small
provided that other processors have more room available. Another
problem arises when a ![]() is reused, but given large enough
is reused, but given large enough ![]() , this
should be rare indeed.
, this
should be rare indeed.
If, somehow, the entire system fills up, a processor should discard small fragments (deep dispersal levels) first. At some future time, this processor will die and be replaced by a new larger one (under our assumption of growth in individual capacities). When this occurs, the repair process will fill in the discarded fragments.
 |
For simplicity, and to emphasize the archival component of our proposal, we have adopted a write-once model in this paper. A read/write model is certainly possible but introduces considerable additional complexity as with replicated databases. It becomes necessary to track versions of each memory block and fragment and the design of caches is complicated. We have come to view the read/write version as a distinct research project with somewhat different potential applications. Finally we remark that a one-time erase operation may be easier to implement but this matter has not been considered in detail.
In our implementation, data written to Intermemory becomes more difficult to erase with every level of replication. The system may send notices to data owners as the replication level increases. An owner may want to keep a copy of the data until the desired level of replication is reached.
The current paper does not address the distributed computation problems of determining when a processor is dead, implementing fault-tolerant DNS, and the protocol for adding new processors and users to the system. Efficient and robust solutions to these problems are crucial for reliable Intermemory.
Another important set of problems is related to permissions and security. In particular, it should be impossible for an adversary to erase or corrupt Intermemory without destroying a very large number of processors. We hope that public-key cryptography can provide acceptable solutions to these problems. Also, we have assumed a simple permission structure in which each subscriber has sole write permission to a set of addresses. We observe that a group permission structure may be needed for some applications. Also, because of the system's archival mission, it may be appropriate to revoke all write permissions after some period of time has passed.
For the Intermemory to function for a very long time and to outlast current software and technology, Intermemory protocols should include a provision for their replacement with new ones, without loss of data.
We have not discussed how new users or new processors join the system. One possible solution is to handle this through a collection of trusted sites in a way similar to that currently used for assigning IP addresses. A related issue is that of policing: When a new user joins the system and is given a block of Intermemory it can write to, the user commits certain resources as a ``payment,'' and the system has to ensure that the user honors this commitment.
In this section we briefly discuss some of the higher level structures that might be built on top of the low-level infrastructure just described.
A distributed file system might be implemented in which Intermemory blocks correspond to disk blocks. This would allow a subscriber to build a directory hierarchy and specific files could then be accessed by incorporating Intermemory software into an application, or more conveniently by deploying daemons that provide an access service that makes Intermemory directories look like standard disk-based directories.
A gateway service could then connect the traditional Web with the Intermemory, i.e., a Web page could link to a document stored there, i.e. within a file system that is itself implemented in Intermemory. In the write-once model such links would have the virtue of never expiring.
A fascinating problem related to Intermemory is the definition of an archival data type system. For example, JPEG is currently a standard image format. However, there is no guarantee that in 100 years a JPEG decoder may be easily accessible. An important type is that of ``program'', that is, an archival representation for a computer program that allows it to be run via emulation at any future time. We envision a simple base machine model and I/O specification on top of which compilers and interpreters can be built. Applications such as data conversion might be written using such a system but we suggest that its utility extends to a much broader class of problems.
One issue to consider is whether a data item should be converted to a new data type as the old one becomes obsolete, or instead be translated whenever it is accessed, using an archival program. Each translation carries with it the finite risk of data loss, and over many years one would therefore expect significant losses to occur with either approach. But in the latter case the original data is still available along with the chain of programs to convert it - so in principle the faulty links in this chain might be repaired. Note that on-demand translation approach might be made transparent to the user.
The Internet emerged without any advance consideration of the search problem. We suggest that a complete Intermemory architecture should consider it up front. Internet search systems operate by indexing document tokens and provisions for this approach must be made. But we suggest that a system of objects might be defined to deal with part of the problem by addressing concepts such as ``who'', ``where'', ``when'', and so on. Some number of these might be a required, or strongly suggested component of every Intermemory document. Beyond these issues rather detailed subject area taxonomies might be developed and maintained by experts so that Intermemory contributions can self classify. Documents without classifications might later be classified by Intermemory robots, or human experts. Even the design of a system of taxonomies that can be revised over the years but remain connected to past versions seems nontrivial and represents an interesting subproblem.
We have identified a general framework and many issues relating to the design of an Intermemory. Preliminary calculations indicate that Intermemory is feasible and practical. That is, one can trade moderate-term commitment of memory resources for archival storage in Intermemory. The detailed design of this system will require the combined efforts of distributed algorithms, cryptography, and systems experts.
In this paper we concentrated on world-wide Intermemory. Archival Intermemories are possible on a smaller scale. For example, a large organization may have an institution-wide Intramemory as a supplement to normal backups; one advantage of this is automated restore operation. Electronic journal publishers may construct an archival journal Intermemory, to ensure that a journal issue is easily available even if its publisher is out of business. Some aspects of small-scale Intermemories, such as security, may be simpler than those for the world-wide Intermemory. A small-scale Intermemory makes a good test case for the first implementation.
A small working group is now meeting regularly at NEC Research Institute to further define Intermemory and work towards implementing it.
The authors thank Baruch Awerbuch, Sam Buss, Jan Edler, Allan Gottlieb, Leonid Gurvits, Joe Kilian, Satish Rao, Scott Stornetta, and Herman Tull, for helpful discussions and comments.
This document was generated using the LaTeX2HTML translator Version 2K.1beta (1.47)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -image_type gif -nonext_page_in_navigation -noprevious_page_in_navigation -up_url ../main.html -up_title 'Publication homepage' -accent_images textrm -numbered_footnotes intermemory.tex
The translation was initiated by Peter N. Yianilos on 2002-06-27