Peter N. Yianilos
July 22, 2001
Netrics, Inc.
pny@netrics.com
(Extended Abstract)
We consider the problem of maximizing certain positive rational functions of a form that includes statistical constructs such as conditional mixture densities and conditional hidden Markov models. The well-known Baum-Welch and expectation maximization (EM) algorithms do not apply to rational functions and are therefore limited to the simpler maximum-likelihood form of such models.
Our main result is a general decomposition theorem that like Baum-Welch/EM, breaks up each iteration of the maximization task into independent subproblems that are more easily solved - but applies to rational functions as well. It extends the central inequality of Baum-Welch/EM and associated high-level algorithms to the rational case, and reduces to the standard inequality and algorithms for simpler problems.
Keywords: Baum-Welch (forward backward algorithm), Expectation Maximization (EM), hidden Markov models (HMM), conditional mixture density estimation, discriminative training, Maximum Mutual Information (MMI) Criterion.
Let ![]() be a directed acyclic graph (DAG) with
be a directed acyclic graph (DAG) with ![]() vertices
vertices
![]() and
and ![]() edges
edges
![]() , having a
single source
, having a
single source ![]() and sink
and sink ![]() .
A nonnegative parameterized weight function is associated with
each edge. The value of a source-sink path is the
product of the weights along it. The value of the graph
is the sum over all source-sink paths, of each path value.
.
A nonnegative parameterized weight function is associated with
each edge. The value of a source-sink path is the
product of the weights along it. The value of the graph
is the sum over all source-sink paths, of each path value.
We refer to such a setting as a simple product flow, and the NP-complete problem of maximizing the graph's value over the weight function parameters [21] corresponds to maximum-likelihood parameter estimation for an HMM, mixture density, and other statistical models. We refer to the ratio of two simple product flows that share the same parameter space as a rational product flow, and the maximization problem corresponds to conditional (discriminative) parameter estimation. That is, a rational product flow consists of two distinct graphs. Its value is the quotient of their values regarding each as a simple product flow. Typically the numerator graph is a subgraph of the denominator induced by the labels provided in the supervised discriminative setting.
The edge weights are a function of a parameter space ![]() containing variable members as well as fixed ones.
In statistical modeling the variables correspond to mixture
element probabilities, symbol output probabilities, state
transition probabilities, the parameters of a Gaussian
density, or other such model components. The fixed parameters
correspond to the data input to the estimation procedure.
In these models an individual edge weight is determined by a
single model component so that it depends on a subset
of the total set of variable parameters - and distinct model
components share no variables.
containing variable members as well as fixed ones.
In statistical modeling the variables correspond to mixture
element probabilities, symbol output probabilities, state
transition probabilities, the parameters of a Gaussian
density, or other such model components. The fixed parameters
correspond to the data input to the estimation procedure.
In these models an individual edge weight is determined by a
single model component so that it depends on a subset
of the total set of variable parameters - and distinct model
components share no variables.
Our product flow setting is an abstraction of these models and
an equivalence class on edges associates each edge ![]() with a weight function denoted
with a weight function denoted ![]() , where
, where ![]() gives
the equivalence class index ranging from
gives
the equivalence class index ranging from ![]() to
to ![]() for
edge
for
edge ![]() .
Each weight function
.
Each weight function ![]() has corresponding parameters
has corresponding parameters
![]() and in general will be associated with many edges.
In the statistical models we're abstracting, the value of a
model component also depends on the edge itself. So our
weight function also accepts the index
and in general will be associated with many edges.
In the statistical models we're abstracting, the value of a
model component also depends on the edge itself. So our
weight function also accepts the index ![]() of edge
of edge ![]() as parameter to capture this dependency.
The weight attached to edge
as parameter to capture this dependency.
The weight attached to edge ![]() is then written
is then written
![]() . For brevity we will
write just
. For brevity we will
write just ![]() .
.
The value of a graph is computed in linear time by visiting
vertices in topological order and accumulating partial results
along the way. This corresponds to the well-known ![]() computation of hidden Markov model evaluation and
reestimation[19,12]. The value
computation of hidden Markov model evaluation and
reestimation[19,12]. The value ![]() recorded at each intermediate vertex
recorded at each intermediate vertex ![]() corresponds to the
sum of all path values from the source to that vertex. The
sink
corresponds to the
sum of all path values from the source to that vertex. The
sink ![]() is visited last and its value
is visited last and its value ![]() is that of
the entire graph.
is that of
the entire graph.
Considering the DAG with all edges reversed and performing the
same algorithm corresponds to the ![]() computation of
HMM reestimation. Here each vertex records the value of
all paths from it to the sink, and the source's value is that
of the entire graph.
computation of
HMM reestimation. Here each vertex records the value of
all paths from it to the sink, and the source's value is that
of the entire graph.
Let edge ![]() connect vertex
connect vertex ![]() with
with ![]() and have weight
and have weight
![]() . Then
. Then ![]() is defined as
is defined as
![]() . This corresponds to the
. This corresponds to the ![]() computation of
HMM reestimation. If the edge weights are interpreted as
probabilities of transiting an edge, then
computation of
HMM reestimation. If the edge weights are interpreted as
probabilities of transiting an edge, then ![]() is the
probability that a random source-sink path passes through edge
is the
probability that a random source-sink path passes through edge
![]() .
.
The Baum-Welch/EM optimization paradigm is iterative. The
value of the graph is regarded as a function of parameter set
![]() , and the goal is to maximize it. The existing
parameter set is denoted
, and the goal is to maximize it. The existing
parameter set is denoted ![]() and is regarded as a fixed
reference during optimization. Based on
and is regarded as a fixed
reference during optimization. Based on ![]() each
iteration begins with the computation of
each
iteration begins with the computation of ![]() values
for each edge.
Based on these
values
for each edge.
Based on these ![]() values,
values, ![]() subproblems are then spawned;
one for each weight function.
subproblems are then spawned;
one for each weight function.
The mathematics of Baum-Welch/EM tell us that any progress
in one or more of these subproblems will strictly
increase the value of the graph.
The value of a graph is a complex interaction of
edge values; each dependent on a weight function
and on the edge itself. The fact that the task of
optimizing a graph's value can be decomposed so
neatly, is in our view the essence of the paradigm.
All interactions are, in effect, sufficiently accounted for
by the ![]() computation.
Commonly used weight functions include discrete probability
functions and Gaussian densities. In both cases simple
and intuitive closed-form solutions exist for these subproblems
- contributing to the popularity of the paradigm.
computation.
Commonly used weight functions include discrete probability
functions and Gaussian densities. In both cases simple
and intuitive closed-form solutions exist for these subproblems
- contributing to the popularity of the paradigm.
Our paper extends the paradigm to rational settings consisting
of a numerator and denominator graph, where ![]() and
and
![]() denote the corresponding edge class functions.
Theorem 2 is our main result. Its equation
3 extends equation 1 to the rational
case by adding a second term. Our extension cleanly addresses
the issue of decomposition, but we know of no simple
closed-form solutions for the subproblems that compare with
those of Baum-Welch/EM. General functional maximization
techniques may be used and specialized techniques represent an
interesting area for future work.
denote the corresponding edge class functions.
Theorem 2 is our main result. Its equation
3 extends equation 1 to the rational
case by adding a second term. Our extension cleanly addresses
the issue of decomposition, but we know of no simple
closed-form solutions for the subproblems that compare with
those of Baum-Welch/EM. General functional maximization
techniques may be used and specialized techniques represent an
interesting area for future work.
There is a long history of developments related to our work. The analysis of [3] marks the generally accepted beginning of the Baum-Welch/EM paradigm and hidden Markov modeling. Essentially the same mathematical idea is found in [9] which introduces EM in the specific context of maximum likelihood mixture density estimation. For completeness we remark that this idea can more generally be viewed as a projection operation with respect to Kullback-Leibler distance [16,7] under Bregman's general framework for convex optimization [6]. This framework is closely related to the later work of I. Csiszár and G. Tusnády [8] and generalizes the much earlier work of [1,18] and also [10,5].
Interest in alternative estimation criteria has grown in recent years and [2] is a notable early milestone in this development. Viewing these more difficult problems in the context of polynomials [11] generalizes Baum-Welch/EM through an embedding that reduces the rational problem to a conventional one. Other work in the area includes the ECM algorithm [17], Hierarchical Mixtures of Experts [15], the CEM algorithm [13], and most recently [14]. Like [11] we consider the problem at an abstract level, but directly derive a different inequality and decomposition result for the rational case.
Jebara and Pentland in [13] (Equation 7) exploit the inequality
![]() to obtain a decomposition result for
simple mixture densities, where the rational form corresponds
to the a posteriori likelihood of a labeled dataset.
Note that throughout this paper natural logarithms are assumed.
Our contribution is the application of this same inequality
together with the inequality of lemma 3 to
give an abstract and general decomposition result. Our result
applies to all models we are aware of within the hidden Markov
model class - to which mixture densities belong as a simple
instance. For mixture densities, our decomposition reduces
to theirs.
to obtain a decomposition result for
simple mixture densities, where the rational form corresponds
to the a posteriori likelihood of a labeled dataset.
Note that throughout this paper natural logarithms are assumed.
Our contribution is the application of this same inequality
together with the inequality of lemma 3 to
give an abstract and general decomposition result. Our result
applies to all models we are aware of within the hidden Markov
model class - to which mixture densities belong as a simple
instance. For mixture densities, our decomposition reduces
to theirs.
Our results are presented abstractly, rather than in the specific context of probability modeling. We suggest that the utility of this abstraction is i) to make clear that the result applies beyond conventional models to noncausal constructions or those with penalty functions, and ii) to provide a simple graph-oriented framework that makes it easier to reason about complex models. The origin of this outlook is [20,21] where the development is limited to the simple (nonrational) case.
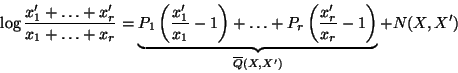 |
(2) |
where
![]() and is equal to zero when
and is equal to zero when
![]() , and
, and
![]() is defined as
the bracketed terms above.
is defined as
the bracketed terms above.
proof: From the elementary inequality
![]() with
equality at
with
equality at ![]() we have that:
we have that:
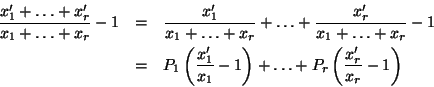
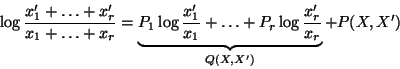
where
![]() and is equal to zero when
and is equal to zero when
![]() , and
, and ![]() is defined as
the bracketed terms above.
is defined as
the bracketed terms above.
proof: For completeness we recast here the well-known elegant proof
originating with [4] into our framework.
Let
![]() , and
, and
![]() .
We must show that
.
We must show that
![]() ,
satisfying the conditions of the lemma.
Now:
,
satisfying the conditions of the lemma.
Now:
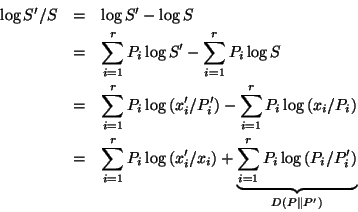
where
![]() is the Kullback-Leibler
distance [16,7] between stochastic
vectors
is the Kullback-Leibler
distance [16,7] between stochastic
vectors ![]() and
and ![]() , which is always nonnegative
and has value zero given equal arguments.
, which is always nonnegative
and has value zero given equal arguments.
![]()
The previous two lemmas give opposing bounds and are combined in the following theorem, which is the first step toward decomposition of our rational optimization problem.
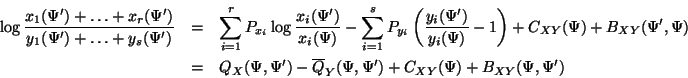
where
![]() , and is zero when
, and is zero when
![]() , and
, and ![]() is constant with respect to
is constant with respect to ![]() .
.
proof:
where
![]() ,
and lemmas 1 and 2
apply to the first two terms giving:
,
and lemmas 1 and 2
apply to the first two terms giving:
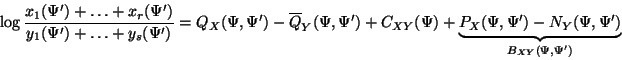
![]()
Each term ![]() and
and ![]() of theorem 1
represents the value of a source-sink path within the DAG.
This value is the product of edge contributions along it.
To decompose the optimization problem our objective is to
rewrite each such product as a sum of edge contributions.
This happens naturally and exactly for the
of theorem 1
represents the value of a source-sink path within the DAG.
This value is the product of edge contributions along it.
To decompose the optimization problem our objective is to
rewrite each such product as a sum of edge contributions.
This happens naturally and exactly for the
![]() function since it is expressed in terms of logarithms.
But the
function since it is expressed in terms of logarithms.
But the ![]() function is more difficult and we
will give a sum decomposition that upper bounds the actual
product value and contacts it when all terms are equal.
function is more difficult and we
will give a sum decomposition that upper bounds the actual
product value and contacts it when all terms are equal.
proof: Since the arithmetic mean is always greater than or equal
to the geometric mean we have:
![]() .
.
![]()
proof: We assume without loss of generality that all source-sink
paths in the denominator DAG are of exactly length ![]() .
This is justified because an equivalent regularized DAG that has
this property can easily be constructed by inserting new dummy
vertices, and dummy edges with constant unity weight as
needed to stretch any short paths.
.
This is justified because an equivalent regularized DAG that has
this property can easily be constructed by inserting new dummy
vertices, and dummy edges with constant unity weight as
needed to stretch any short paths.
Next consider a source-sink path ![]() in the denominator graph
and let
in the denominator graph
and let ![]() denote the set of edges along it.
Let the value of this path correspond to a single term
denote the set of edges along it.
Let the value of this path correspond to a single term ![]() of
theorem
1. Then:
of
theorem
1. Then:
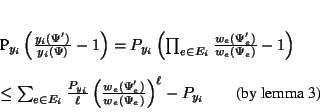
Now each edge ![]() in the denominator graph occurs in many
source-sink paths. Summing the
in the denominator graph occurs in many
source-sink paths. Summing the ![]() over all paths passing through edge
over all paths passing through edge ![]() yields
yields
![]() . Then observing that the subtraction of
. Then observing that the subtraction of ![]() does
not affect the optimization yields the additive term:
does
not affect the optimization yields the additive term:
for each edge. Starting from lemma 2, which
is applied to the numerator graph, and summing over all paths
containing an edge ![]() yields the additive term
yields the additive term
![]() . Subtracting the denominator
term above from this, and grouping by weight function completes the proof.
. Subtracting the denominator
term above from this, and grouping by weight function completes the proof.
![]()
Using Baum-Welch/EM, multiple observations are dealt with by
adding their corresponding ![]() functions. The same is true in
our more general rational setting by adding
functions. The same is true in
our more general rational setting by adding ![]() as
well. The DAG depth
as
well. The DAG depth ![]() is then related to the complexity
of processing of a single observation. For simple mixture
models
is then related to the complexity
of processing of a single observation. For simple mixture
models ![]() (see explanation below), and for HMMs
(see explanation below), and for HMMs
![]() where
where ![]() is the number of time series elements
comprising a single observation in the training set.
is the number of time series elements
comprising a single observation in the training set.
The DAG for a simple mixture density is easily described.
Each of the edges outbound from the source select a mixture
component, and each edge's weight is the probability of that
component. Each edge then leads to an interior vertex with
in-degree one. From that vertex a single outbound edge leads
to the sink. Its weight is the observation's probability
given the corresponding density function. Hence ![]() for
mixture densities since all source-sink paths are of this
length.
for
mixture densities since all source-sink paths are of this
length.
So our result gives a new form of CEM [13] where both
mixture coefficients and density models are optimized in a
single step. If they are trained one-by-one, then ![]() and our decomposition is equivalent to Equation 7
of [13].
and our decomposition is equivalent to Equation 7
of [13].
Returning to more complex models such as HMMs, we remark that
if a single observation is made up of a long series of
elements, then ![]() can become prohibitively large and
reduce the step size that is possible using our results. There
are two general strategies that might be used to combat this
effect: 1) break-up a single iteration into subiterations that
optimize weight functions one-by-one (
can become prohibitively large and
reduce the step size that is possible using our results. There
are two general strategies that might be used to combat this
effect: 1) break-up a single iteration into subiterations that
optimize weight functions one-by-one (![]() ), or in groups; in
both cases recomputing
), or in groups; in
both cases recomputing ![]() values between subiterations,
2) develop an adaptive algorithm that searches for a reduced
values between subiterations,
2) develop an adaptive algorithm that searches for a reduced
![]() value that nevertheless allows the optimization to make
progress.
value that nevertheless allows the optimization to make
progress.
At our level of abstraction little can be said regarding convergence. We do know that strictly greater product-flows will result given strict progress in any of the subproblems, so that if the flow value is bounded (as it is for any probability model) then convergence of this value is ensured. But this does not imply convergence of model parameters. Saying more about this requires that something more be assumed about the weight functions themselves, and is beyond the scope of this paper.
It must be said that by extending to the rational case we leave behind a splendid property of conventional Baum-Welch/EM. Namely, that for common weight functions such as normal densities or discrete probability functions, the subproblems resulting from decomposition have globally optimal solutions that are trivially computed in closed form. Still, efficient approaches do sometimes exist. In [13] the authors consider simple mixtures of unnormalized Gaussians, and do not attempt to train all parameters simultaneously. The result is a practical prescription for this setting. General techniques for subproblem optimization is an interesting area for future work, but is beyond the scope of this paper.
Still, our work cleanly settles the issue of decomposition at a level of generality that includes all discrete-state models that the author is aware of within the hidden Markov family. In addition we suggest that our graph-based product-flow outlook makes it easier to reason about complex models and see, for example, that the paradigm's decomposition mathematics apply directly to variations including noncausal models, and penalized constructions that impose soft parsimony constraints such as MDL and MAP.
The author thanks Dan Gindikin and Sumeet Sobti for their comments on this manuscript, and Eric Sven Ristad with whom the original DAG-based outlook for simple product flows was developed.
This document was generated using the LaTeX2HTML translator Version 2K.1beta (1.47)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -image_type gif -nonext_page_in_navigation -noprevious_page_in_navigation -up_url ../main.html -up_title 'Publication homepage' -numbered_footnotes gbw.tex
The translation was initiated by Peter N. Yianilos on 2002-06-22