Eric Sven Ristad - Peter N. Yianilos
Research Report1 CS-TR-533-96
December, 1996 (revised April 1997)
Restricted to probabilistic form, FGMs correspond to stochastic automata that allow observations to be processed in many orderings and groupings - not just one-by-one in sequential order. As a result the parameters of a highly general form of stochastic transducer can be learned from examples, and the particular case of string edit distance is developed.
In the FGM framework one may direct learning by criteria beyond simple maximum-likelihood. The MAP (maximum a posteriori estimate) and MDL (minimum description length) are discussed along with the application of FGMs to causal-context probability models and unnormalized noncausal models.
Keywords:Expectation Maximization (EM), Hidden Markov Model (HMM), Baum-Welch Reestimation, Stochastic: Model, Grammar, Transducer, Transduction, Metric Learning, Maximum Likelihood (ML), Maximum a Posteriori (MAP), Minimum Description Length (MDL), String Edit Distance, String Similarity.
Hidden discrete-state stochastic approaches such as hidden Markov models (HMM) for time series analysis, stochastic context free grammars (SCFG) for natural language, and statistical mixture densities are used in many areas including speech and signal processing, pattern recognition, computational linguistics, and more recently computational biology. These are parametric models and are typically optimized using the Baum-Welch, inside-outside, and expectation maximization (EM) algorithms respectively. They share a common mathematical foundation and are shown to be instances of a single more general abstract recursive optimization paradigm which we refer to as the finite growth model framework (FGM) involving non-negative bounded functionals associated with finite directed acyclic graphs (DAG). These functionals need not be probabilities and an FGM need not correspond to a stochastic process.
With FGMs interesting new kinds of stochastic models may be designed, existing models may be improved, settings that are not strictly probabalistic in nature may be addressed, and it becomes easier to design and reason about a wide range of problems. This paper introduces and develops the FGM framework and then applies it to:
Graphical models [20,27] represent a branch of related work in which the independence structure of a set of random variables is the main focus. One can express such models using FGMs - as well as considerably more general settings such as that in which no two variables are independent (their graphical model is fully connected), but they are jointly constrained in interesting ways.
An FGM is a directed acyclic graph with a single source and sink
together with a collection of non-negative bounded weight functions ![]() that are associated with edges - one per edge. The value of a
source-sink path is the product of the weights along it and the FGM's
value is the sum over all such paths of their values. Section
0.2 presents a formal development but we will sketch the
basic ideas here.
that are associated with edges - one per edge. The value of a
source-sink path is the product of the weights along it and the FGM's
value is the sum over all such paths of their values. Section
0.2 presents a formal development but we will sketch the
basic ideas here.
The weight function
![]() associated with edge
associated with edge ![]() accepts
an argument
accepts
an argument ![]() and parameters
and parameters ![]() . The objective of FGM
optimization is to maximize the FGM's value over its parameters
. The objective of FGM
optimization is to maximize the FGM's value over its parameters ![]() which are assumed to be independent. The argument
which are assumed to be independent. The argument ![]() is regarded
as fixed. The same weight function may be associated with several
edges but will in general assume different values since
is regarded
as fixed. The same weight function may be associated with several
edges but will in general assume different values since ![]() is a
function of the edge to which it is attached.
is a
function of the edge to which it is attached.
If each edge has a distinct associated weight function then optimization
is immediately reduced to the task of independently maximizing the
weight functions in isolation. The interesting situation arises when
this is not the case. Here a change to a single parameter set ![]() may affect weights throughout the DAG. The values of many source-sink
paths may be affected and an interaction between members of
may affect weights throughout the DAG. The values of many source-sink
paths may be affected and an interaction between members of ![]() arises, i.e. simple independent maximization is no longer possible.
arises, i.e. simple independent maximization is no longer possible.
Surprisingly it is still possible to decompose the optimization problem into certain independent subproblems. This is the key mathematical message of Baum-Welch and EM generalized to the FGM framework. However, even exact solution of the subproblems does not yield a maximum for the FGM. But a new combined parameter set does result that strictly improves it -- unless one has already converged to a limiting value. Iteration is then used to climb to such a limiting value. Unlike gradient descent with line search this approach confidently moves to a sequence of increasingly better points in parameter space and in many cases reduces to a strikingly simple and intuitive algorithm. The cost functions may themselves be FGMs and the computation of an improved parameter set simply depends upon the ability to solve the primitive maximization problems at the bottom of the recursive hierarchy.2
The mathematical idea behind this decomposition begins with a simple
equality having to do with the ![]() of a sum of terms. Let
of a sum of terms. Let
![]() and define proportions
and define proportions ![]() . Notice
. Notice ![]() . For any nonnegative vector
. For any nonnegative vector ![]() with unity sum:
with unity sum:
Observe that the second term is
maximized when ![]() since both are stochastic vectors.
since both are stochastic vectors.
In our setting each term ![]() corresponds to a source-sink path, and
its value is not constant, but rather is a function of some parameter
set
corresponds to a source-sink path, and
its value is not constant, but rather is a function of some parameter
set ![]() . Optimizing the FGM is then the problem of maximizing
their sum over
. Optimizing the FGM is then the problem of maximizing
their sum over ![]() . This is the same as optimizing their
. This is the same as optimizing their ![]() sum; connecting the equality above to the problem of FGM optimization.
sum; connecting the equality above to the problem of FGM optimization.
Accordingly we parameterize the equality by writing
![]() and
and
![]() where our objective is to maximize
where our objective is to maximize ![]() over
over ![]() .
The search for a maximum takes place iteratively. During each iteration we denote
the current parameters by
.
The search for a maximum takes place iteratively. During each iteration we denote
the current parameters by ![]() and vary
and vary ![]() looking
for an improved set.
looking
for an improved set.
To express this iterative approach the equality is specialized by
defining ![]() to be
to be ![]() evaluated at the current parameters
evaluated at the current parameters ![]() ,
i.e.
,
i.e.
![]() . Then:
. Then:
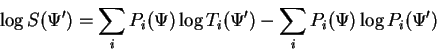
The right term may be ignored because any departure from ![]() will decrease it whereby
will decrease it whereby ![]() and therefore
and therefore ![]() are increased.
We then focus on maximizing the left term which
corresponds to the
are increased.
We then focus on maximizing the left term which
corresponds to the ![]() function of the HMM/EM literature.
function of the HMM/EM literature.
Elements of the remaining summation correspond to source-sink paths
through the FGM's DAG and the proportions ![]() are the relative
contribution of each path to the FGM's value.
Each term
are the relative
contribution of each path to the FGM's value.
Each term
![]() is then a product of of weight functions and
breaks up into a sum of individual
is then a product of of weight functions and
breaks up into a sum of individual ![]() terms. The proportions
are then distributed over them and the final step is to group
terms by weight function. The problem is then decomposed as required
into independent subproblems each involving a single weight function.
terms. The proportions
are then distributed over them and the final step is to group
terms by weight function. The problem is then decomposed as required
into independent subproblems each involving a single weight function.
The argument above is made in much greater detail in section 0.2
and the formal definition of an FGM presented there is more involved
in two respects. First, there are two weight functions, not one, associated
with each edge. These are abstractions of the normally separate transition
and observation generation functions of a stochastic automaton.
Second, the ![]() in our discussion above is defined to be some function
of an observation tuple
in our discussion above is defined to be some function
of an observation tuple ![]() . A simple such function is that of coordinate
projection where, for example, the function's value might be
that of a single dimension of
. A simple such function is that of coordinate
projection where, for example, the function's value might be
that of a single dimension of ![]() .
.
The contribution of section 0.2 is the development of a framework that has nothing directly to do with stochastic models or probability in which the essential ideas of Baum-Welch and EM nevertheless apply. Our view is that the essential content of these ideas is one of decomposability of certain optimization problems that are captured in a somewhat general way by our definition of an FGM.
The early literature, especially theorem 2.1 of [3], reveals an awareness that the mathematics of HMMs apply beyond strictly probabalistic settings. This direction of generalization does not however appear to have been followed until now. Thinking seems to have been dominated by the motivating problem: the optimization of Markovian stochastic models. Because of the limited computational capabilities of the time and their highly mathematical viewpoint a great deal of emphasis was also placed on the primitive weight functions for which exact maximization may be performed in closed form, and those which give rise to unique global maxima. By contrast we devote very little attention to the the specific characteristics of these primitive functions and view them instead as an abstract types that by assumption support a set of required operations.
In section 0.3 the FGM framework is specialized to
the case of probabilistic models. The ![]() above result from
projections that select one or more coordinate dimensions such that
along each source-sink path each dimension is selected exactly once.
Also, the weight functions are restricted to be probability functions
or densities. It is not important that the dimensions occur in any
fixed order as one follows alternative source-sink routes; nor is it
required that the dimensions be selected one at a time. The
contribution of this outlook is that FGM-based stochastic models can
generate observations in many orderings and groupings - not just
one-by-one in sequential order as in HMMs - a capability
exploited later in our discussion of stochastic transducers.
above result from
projections that select one or more coordinate dimensions such that
along each source-sink path each dimension is selected exactly once.
Also, the weight functions are restricted to be probability functions
or densities. It is not important that the dimensions occur in any
fixed order as one follows alternative source-sink routes; nor is it
required that the dimensions be selected one at a time. The
contribution of this outlook is that FGM-based stochastic models can
generate observations in many orderings and groupings - not just
one-by-one in sequential order as in HMMs - a capability
exploited later in our discussion of stochastic transducers.
Section 0.4 begins by considering the case of infinite stochastic processes. Viewed generatively these models produce output of unbounded size but are used in practice to evaluate the probability of finite observations and are trained using a finite set of finite observations. Restricted in this way they correspond to FGMs that capture their truncated form. Moreover the conventional evaluation and learning algorithms associated with them arise naturally from this viewpoint.
Baum-Welch and EM are today regarded as maximum-likelihood parameter estimation techniques. A more modern learning theoretic perspective recognizes the important tension between model complexity and available training data. An important contribution of section 0.4 is the description of a construction that modifies the FGM associated with a stochastic model so that alternative criteria such as MDL or MAP can guide optimization. The optimization is still based on Baum-Welch/EM so we suggest that these should not be viewed as statistical ML techniques and that their broader utility is revealed by our more general functional optimization perspective.
The observation functions associated with each state in a conventional Hidden Markov model must satisfy an independence assumption: that their state dependency is limited to the current state (the Markov condition). Section 0.4 observes that conditioning on earlier portions of the observation sequence does not violate this assumption and demonstrates that using the FGM framework, it is easy to see that parameter reestimation for such context dependent HMMs decomposes into primitive context optimization problems. This generalizes Brown's use [7] of the previous speech window to condition generation of the current one. Thus the power of causal context models such as statistical language models may be added to the HMM framework and may lead to improved performance.
The section also presents another illustration that the reach of FGMs extends in a useful way beyond conventional and strictly stochastic models. Causal context models express the probability of an observation as a product of conditional probabilities such that each dimension is predicted once and does appear earlier as a conditioning variable. These restrictions are constrictive in settings such as image modeling where modeling each pixel based on its surrounding context seems natural. Simply relaxing the requirements that probabalistic modeling places on an FGM's source-sink projection functions proves that FGM optimization will improve even noncausal models like the image example above.
Stochastic models describe the manner in which an object is generated. This object is conventionally imagined to be something like an image, an audio recording, or a string of symbols. If instead one models pairs of such objects the focus shifts from describing the nature of an individual to uncovering the relationship between them. The pairs may be thought of as instances of the are similar concept and learning an effective model to describe them is an example of what the authors have called the metric learning paradigm.
Fixing the left element of the pair one might then ask what generative
sequences could explain the right. This is the essential idea of
![]() -way stochastic transduction. Section 0.5
shows that a somewhat general automaton-based definition for
-way stochastic transduction. Section 0.5
shows that a somewhat general automaton-based definition for ![]() -way
transduction may be reduced to problems within the FGM framework. One
may view speech recognition as a transduction,
perhaps in several stages, and the application of learned transducers
to this field represents an interesting area for future work.
-way
transduction may be reduced to problems within the FGM framework. One
may view speech recognition as a transduction,
perhaps in several stages, and the application of learned transducers
to this field represents an interesting area for future work.
Perhaps the best known example of ![]() -way transduction is that of string edit distance which is defined as the least costly way to
transform one string into another via a given set of weighted
insertion, deletion, and substitution editing operations. The
development in section 0.5.1 begins with a natural
reformulation into stochastic terms first noted by Hall and Dowling in
[12, P.390-1]. We refer to the result as stochastic edit
distance [24].
-way transduction is that of string edit distance which is defined as the least costly way to
transform one string into another via a given set of weighted
insertion, deletion, and substitution editing operations. The
development in section 0.5.1 begins with a natural
reformulation into stochastic terms first noted by Hall and Dowling in
[12, P.390-1]. We refer to the result as stochastic edit
distance [24].
Our focus is on the interesting problem of learning insert, delete,
and substitute costs from a training corpus
![]() of string pairs. The objective is to minimize the total
stochastic edit distance of the collection. In [24] the
authors give such a learning algorithm independent of the FGM
framework and report on experiments. Until now the costs which
parameterize edit distance algorithms have been prescribed not
learned. Section 0.5.1 of this paper describes the
reduction of this learning problem to the FGM optimization framework
and may be viewed as an adjunct to [24] providing a proof of
correctness.
of string pairs. The objective is to minimize the total
stochastic edit distance of the collection. In [24] the
authors give such a learning algorithm independent of the FGM
framework and report on experiments. Until now the costs which
parameterize edit distance algorithms have been prescribed not
learned. Section 0.5.1 of this paper describes the
reduction of this learning problem to the FGM optimization framework
and may be viewed as an adjunct to [24] providing a proof of
correctness.
The optimized costs are often quite different from the initial ones. It is in this sense that we learn them. In previous work, the costs have been stipulated after study of the problem domain. Even worse, maximally uninformative unit costs (i.e., Levenshtein distance) are sometimes stipulated when the problem domain is nontrivial. It is now possible to improve any educated guess, or start virtually from scratch from unit costs, to arrive at a set of optimized ones. Algorithms 7 and 8 of section 0.5.1 run in time proportional to the product of the two string lengths, matching the complexity of the conventional edit distance computation. Since edit distance has found widespread application our discovery of a simple way to learn costs may lead to improved performance in many problem areas.
Section 0.5.1 also observes that the notion of string edit distance may be strengthened so that the cost of an edit operation depends not only on its target but also on context. For example, such context-sensitive string edit distances allow the cost of inserting a symbol to depend on the symbol left-adjacent to the insertion site. The result remains an FGM on one therefore the ability to easily improve costs given a training corpus is retained.
Several kinds of hidden discrete-state stochastic models are in widespread use today. Hidden Markov Models (HMM) were introduced in the 1960's [2,3,1] and are typically applied in time-series settings when it is reasonable to assume that the observed data are generated or approximated well by the output of an automaton which changes state and generates output values stochastically. A matrix-based approach is typically used to formalize this notion, and [21] and [14] provide nice overviews. Normal (Gaussian) mixtures find application in statistical pattern recognition where items to be classified are represented as real-valued vectors. Stochastic context free grammars (SCFG) lead to a natural probabilistic interpretation of natural language parsing. Other model types exist, and are easily formed by combining and modifying the standard ones.
The situation is complicated by parameter tying; the practice of reducing the number of parameters in a model by equating two or more different sets of formal parameters to a single set. Observations are sometimes discrete and sometimes continuous. Entire models may be mixed together or recursively combined. Some states or transitions may be nonemitting meaning that no observation is generated. Finally, nonuniform time-series models may predict several future data points. All of these factors make it difficult to write down a single high-level framework with which to reason about and verify the correctness of a model's associated algorithms.
The contribution of FGMs is to move instead to a lower-level representation which is common to all of the models and complicating variations above. As noted earlier isn't really the original model which is represented, but rather its truncation to the given collection of finite observations. By understanding FGMs it is possible to reason about the others as mappings from their individual description language to an FGM given finite observations.
Section 0.6 relates the models above to FGMs by describing a reduction for each. As further illustration it considers the portfolio optimization problem and shows that the simple iterative algorithm reported in [9] for optimization arises by reducing the problem to an FGM.
The work described in this paper began in 1993 with our efforts to model handwriting. The focus then was on transduction, in an attempt to evaluate and learn a notion for similarity for the off-line case. This effort exposed many limitations of the conventional modeling outlook - problems that extend far beyond handwriting. To address these limitations we had to break several rules of conventional modeling only to ultimately discover that these rules are in many cases unnecessary artifacts of the history that led to HMMs and EM. After three years of generalization, and exercises in specialization, we arrived at the FGM outlook reported here.
In this section we develop the theory of Finite Growth Models (FGM) as a class of nonnegative functionals represented as annotated directed acyclic graphs. The next section focuses on the special case of probability models. Our formal definition of an FGM amounts to an intricate recursive data structure, in the computer science sense, that has been crafted to span a wide range of applications. As a result it may seem at first to be rather abstract and have little to do with stochastic modeling, but each feature is an abstraction of some characteristic required by a problem we considered. It is the mathematical engine at the center of these problems. In particular much of our development and notation parallels that of Hidden Markov Models (HMM).
Let ![]() be a tuple observation with components
be a tuple observation with components
![]() , and
, and
![]() denote the space of all such observations. We will not
specify the type of each component since for much of our development
it matters only that appropriate functions exists on the space of
values that a component may assume. Components may therefore
represent discrete values such as letters of the alphabet, continuous
values such as real numbers, or other more complex structures. Within
the observation tuple, component types need not be the same. In
simple time series probability-model settings, components do
have the same type, and position within the tuple corresponds to the
passage of time.
denote the space of all such observations. We will not
specify the type of each component since for much of our development
it matters only that appropriate functions exists on the space of
values that a component may assume. Components may therefore
represent discrete values such as letters of the alphabet, continuous
values such as real numbers, or other more complex structures. Within
the observation tuple, component types need not be the same. In
simple time series probability-model settings, components do
have the same type, and position within the tuple corresponds to the
passage of time.
The choice value corresponding to an edge
![]() is then
is then
![]() and
is denoted
and
is denoted ![]() for brevity where it is
understood that in this context
for brevity where it is
understood that in this context ![]() refers to
refers to
![]() - but the subscript is sometimes
written for clarity.
- but the subscript is sometimes
written for clarity.
The combined observation and choice parameters are
denoted ![]() and
and ![]() respectively, and
respectively, and
![]() denotes the parameters of
denotes the parameters of ![]() .
The value of a source-sink path is the product of
the observation and choice functional values along it. The
value
.
The value of a source-sink path is the product of
the observation and choice functional values along it. The
value ![]() of the FGM is the sum over all
source-sink paths, of the value of each.
A choice or observation model whose value is the constant
of the FGM is the sum over all
source-sink paths, of the value of each.
A choice or observation model whose value is the constant ![]() does
not affect an FGM's value and is therefore said to be
void.
does
not affect an FGM's value and is therefore said to be
void.
Notice that since an FGM is itself a nonnegative parameterized functional, the definition above may be applied recursively to define an FGM whose constituent functionals are themselves FGMs.
Direct evaluation of an FGM's value by enumerating all source-sink
paths is of course not practical. Fortunately ![]() may be
efficiently computed using dynamic programming. To express this
precisely requires some notation. Let
may be
efficiently computed using dynamic programming. To express this
precisely requires some notation. Let
![]() be a
topologically sorted vertex listing. Following the convention of the
HMM literature, we define corresponding real variables
be a
topologically sorted vertex listing. Following the convention of the
HMM literature, we define corresponding real variables
![]() . The sets of edges into and out
from a vertex
. The sets of edges into and out
from a vertex ![]() are denoted by
are denoted by ![]() and
and ![]() respectively. Using the notation above, the contribution of an edge
respectively. Using the notation above, the contribution of an edge
![]() to the value of a path containing it, is
to the value of a path containing it, is
![]() The product of these contributions is the probability of
the path. The complete dynamic program is then given by the following
simple algorithm:
The product of these contributions is the probability of
the path. The complete dynamic program is then given by the following
simple algorithm:
This may be recognized as the forward step of the Baum-Welch HMM forward-backward algorithm [2,1,21] adapted to the
more general FGM setting. Following execution ![]() has value
has value
![]() .
.
Algorithm 1 is said to evaluate the FGM using its current set of parameters. The optimization problem we consider seeks a parameter set that maximizes the FGM's value
but we will be content to find locally optimal solutions,
and in some cases to simply make progress. Here ![]() is fixed and it
is the FGM's parameters that are varied.
is fixed and it
is the FGM's parameters that are varied.
The end-to-end concatenation of two FGMs clearly results in another
whose value is the product of the two, so that given a set of
observations
![]() , the optimization problem
, the optimization problem
is really just an instance of Eq. 4. Viewing
![]() as training examples the optimization then learns a
parameter set, or in the language of statistics and assuming the FGM
corresponds to a probability model, estimates its parameters.
as training examples the optimization then learns a
parameter set, or in the language of statistics and assuming the FGM
corresponds to a probability model, estimates its parameters.
Our approach to this problem extends the idea of Baum-Welch to FGMs. Several years following the development of HMMs, essentially the same mathematical ideas expressed in the their algorithm were rediscovered as the expectation maximization (EM) algorithm for mixture densities [11,22]. This work focused on parameter estimation for mixture densities, and has had considerable influence on a somewhat independent community. In what follows we will use the phrase Baum-Welch/EM to refer to the adaptation of these results to the FGM setting.
The HMM and EM literature deals with probabalistic models, and Baum-Welch/EM is presented as a method for reestimating their parameters. Our mathematical contribution is the recognition that the method is not essentially a statement about probability but rather should be viewed as an iterative approach to the maximization of arbitrary parameterized nonnegative functionals of a certain form. The form consists of a sum of terms each one of which is a product of subterms. An FGM's DAG is a representation of these forms which, for many with appropriate structure, has the advantages of succinct representation and computational economy. In the interesting case, the subterms are partitioned or grouped into families sharing common parameters. The approach then consists of focusing on each family in isolation thus localizing the problem. Individual family maximization problems are constructed that include certain weighting factors. These factors are constant with respect to the family's optimization but are computed using the entire DAG and are therefore influenced by all families. Thus global information is used to decompose the original problem - localizing it to individual families. If parameters are found that improve any of the individual family problems, the FGM's value will strictly increase. The method is iterative since even exact maximization of every family's problem may not maximize the FGM's value. Instead the process is repeated.
To formalize this idea of simply making progress with respect to a given maximization problem, the notation:
is introduced. Notice that the improvement need not be strict and that the result is a set of values.
Our definition of an FGM is clearly an abstraction of stochastic modeling. We remark that it is possible to start from a definition that is yet more general and in a sense simpler in which only choice models are used and a variable number may be attached to each edge. But then connecting our results to the mainly stochastic problems we are interested in becomes more complex, and it is more difficult to see the connection between our generalization and the original literature.
We therefore develop Baum-Welch/EM for FGMs starting from a lemma that is stated so as to illustrate its correspondence with the EM literature. It is a statement about improper mixture densities, i.e. where the whole and its constituent parts are not necessarily probabilities. This is relevant to FGMs because they may be regarded as immense mixtures of contributions from every source-sink path. We follow earlier lines in its proof without requiring proper densities. The lemma may also be derived starting from theorem 2.1 of [3] in its most general form.
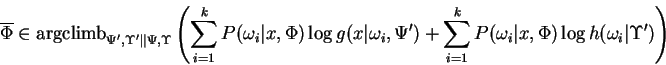
proof: We begin by establishing the identity:
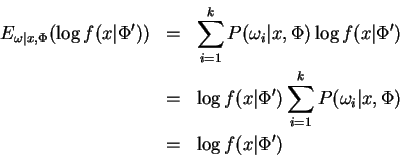
where ![]() is viewed as a discrete random variable distributed
as
is viewed as a discrete random variable distributed
as
![]() and
and
![]() denotes expectation
with respect to it. The point is merely that
denotes expectation
with respect to it. The point is merely that
![]() is independent
of
is independent
of ![]() since the former depends on
since the former depends on ![]() not
not ![]() .
.
Next with
![]() we have
we have
![]() since
since
![]() . So:
. So:
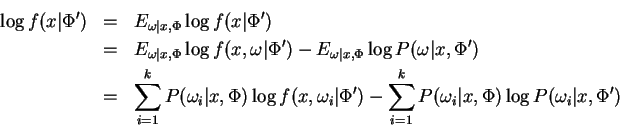
It follows from Jensen's inequality that the second
summation is minimized by
![]() . This can also be
seen by recognizing it as
. This can also be
seen by recognizing it as
![]() , where
, where
![]() is the Kullbak-Leibler distance, and
is the Kullbak-Leibler distance, and
![]() denotes entropy (see [10]). Thus
maximizing the first term, written
denotes entropy (see [10]). Thus
maximizing the first term, written
![]() in the
literature, will surely increase
in the
literature, will surely increase
![]() and hence
and hence
![]() . But:
. But:
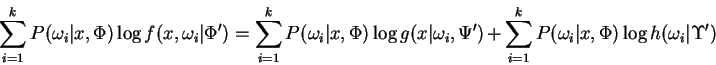
and the right side is recognized as the object of
the
![]() operator in the lemma's statement.
operator in the lemma's statement.![]()
The conditional expectation operator
![]() can cause
confusion but we use it to make clear the correspondence with the EM
literature. Our discussion in section 0.1 starting with
Eq. 1 represents an alternative approach that is free of
explicit mention of expectation and probability.
can cause
confusion but we use it to make clear the correspondence with the EM
literature. Our discussion in section 0.1 starting with
Eq. 1 represents an alternative approach that is free of
explicit mention of expectation and probability.
To apply lemma 1 to FGM optimization we introduce two
more simple algorithms. The first computes ![]() by sweeping
through the DAG's vertices in reverse rather than forward order,
establishing the values of a new set of real variables
by sweeping
through the DAG's vertices in reverse rather than forward order,
establishing the values of a new set of real variables
![]() :
:
This corresponds to the backward step of the forward-backward algorithm. After
it has run, ![]() equals
equals ![]() , and therefore
, and therefore ![]() .
.
We denote by
![]() the source-sink paths
through
the source-sink paths
through ![]() , and by
, and by ![]() the set of edges along
a particular path
the set of edges along
a particular path ![]() , and by
, and by ![]() the set of paths that include
edge
the set of paths that include
edge ![]() . The contribution of a single path
. The contribution of a single path ![]() to the
overall value of the FGM is denoted
to the
overall value of the FGM is denoted
![]() and given by:
and given by:
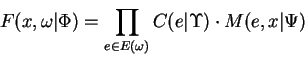
So that:
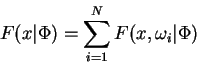
Next define
![]() , and
then for each edge
, and
then for each edge ![]() define:
define:
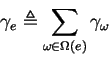
Notice that by definition the ![]() arise from a partition of the
set of all source-sink paths whence it is clear that:
arise from a partition of the
set of all source-sink paths whence it is clear that:
The ![]() and
and ![]() variables may be used to compute these
variables may be used to compute these ![]() via a third simple dynamic program corresponding to the expectation step
of EM:
via a third simple dynamic program corresponding to the expectation step
of EM:
where either ![]() or
or ![]() may be substituted for
may be substituted for
![]() . As a practical matter algorithms 3 and
2 may be combined.
. As a practical matter algorithms 3 and
2 may be combined.
We are now in position to state precisely how the objective of optimizing an FGM is decomposed into smaller problems.
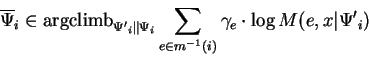
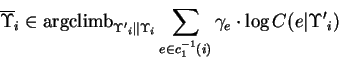
where the ![]() are computed based on
are computed based on
![]() .
The exact Baum-Welch/EM reestimate is formed by replacing
the
.
The exact Baum-Welch/EM reestimate is formed by replacing
the
![]() operations with
operations with
![]() . By
. By ![]() and
and
![]() we mean the set valued inverses of functions
we mean the set valued inverses of functions ![]() and
and ![]() .
.
The exact form corresponds to the historical definition of the Baum-Welch/EM reestimate. However, since this paper's focus is on decomposition, and not mathematical issues relating to particular choice and observation models, we will use ``Baum-Welch reestimate'' to refer to our inexact form defined above. This allows our framework to include models for which exact solution is not convenient. Also it is interesting to note that one may choose to not reestimate one or more models, and still improve the overall FGM.
proof: We write:
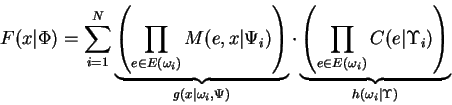
which makes clear the correspondence between the FGM
and lemma 1. Now by their definitions
![]() so from the lemma we
have:
so from the lemma we
have:
![\begin{displaymath}
\overline{\Phi}\in \mathrm{arg max}_{{\Phi^\prime}, {\Upsil...
...\in E(\omega_i)} C(e\vert{\Upsilon^\prime}_i) \right) \right]
\end{displaymath}](img166.gif)
![\begin{displaymath}
\overline{\Phi}\in \mathrm{arg max}_{{\Phi^\prime}, {\Upsil...
... \gamma_{\omega_i} \log C(e\vert{\Upsilon^\prime}_i)
\right]
\end{displaymath}](img167.gif)
The double summations above enumerate every edge along every path though the FGM. To complete the proof we have only to enumerate them in a different order:
![\begin{displaymath}
\overline{\Phi}\in \mathrm{arg max}_{{\Phi^\prime}, {\Upsil...
...(e)} \gamma_\omega \log C(e\vert{\Upsilon^\prime}_i)
\right]
\end{displaymath}](img168.gif)
Recall
![]() so:
so:
![\begin{displaymath}
\overline{\Phi}\in \mathrm{arg max}_{{\Phi^\prime}, {\Upsil...
... \gamma_e \log C(e\vert{\Upsilon^\prime}_i)
\right)
\right]
\end{displaymath}](img170.gif)
and the parenthesized terms are
the independent subproblems of definition 2.![]()
We now change our focus to computational and data structural issues. The first part of our discussion deals with the intricacies of recursion. That is, when an FGM invokes another FGM as one of its observation models. Here, proper algorithm and data structure design can lead to polynomial rather than exponential complexity as illustrated by the case of stochastic context free grammars described in section 0.6.2. We will confine ourselves to finite recursion. The second issue has to do with the arithmetic demands of FGM computation.
The idea behind reducing the complexity of recursive FGM operations is a simple one: avoid duplicate work. If a particular combination of an observation model and selection function occurs multiple times, the combination should only be evaluated once. Since choice models do not depend on the observation, each should be evaluated only once. The computation is then ordered so that when an edge is considered, its choice and observation functions have already been evaluated and their values may be looked up in constant time.
To formalize this idea recall that ![]() is defined as
is defined as
![]() . Notice that edge
. Notice that edge ![]() appears as a function argument. We say
appears as a function argument. We say
![]() if their definitions are the same. Each equivalence
class is referred to as a model application and expressing
algorithms in terms of these classes avoids duplicate work. If for
two edges
if their definitions are the same. Each equivalence
class is referred to as a model application and expressing
algorithms in terms of these classes avoids duplicate work. If for
two edges
![]() then by this definition
then by this definition
![]() - even if
- even if
![]() is the same function as
is the same function as
![]() .
For this reason we adjust the definition to account for equivalences
that may exist among the
.
For this reason we adjust the definition to account for equivalences
that may exist among the ![]() .
.
This adjustment is subtle and we therefore illustrate it by example.
Suppose that the observation model associated with an edge ![]() of
the top level FGM is itself an FGM
of
the top level FGM is itself an FGM ![]() and that selection function
and that selection function
![]() is used by
is used by ![]() . Now within
. Now within ![]() assume that some edge
assume that some edge ![]() uses an observation model
uses an observation model ![]() with selection function
with selection function ![]() . Then to
evaluate
. Then to
evaluate ![]() , selection functions
, selection functions ![]() and
and ![]() are composed. Now
focus on another top level edge
are composed. Now
focus on another top level edge ![]() to which an FGM
to which an FGM ![]() is
attached using selection function
is
attached using selection function ![]() . Within
. Within ![]() consider an edge
consider an edge
![]() using the same observation model
using the same observation model ![]() as does
as does ![]() , but in
combination with selection function
, but in
combination with selection function ![]() . To evaluate
. To evaluate ![]() here
here ![]() and
and ![]() are composed. So
are composed. So ![]() should only be evaluated once if
should only be evaluated once if
![]() and
and
![]() are the same function. This
may be the case despite the fact that
are the same function. This
may be the case despite the fact that ![]() and
and ![]() are not. Thus,
whenever possible, equivalence classes should be defined so as to
account for possibly equivalent compositions of selection functions.
This is easily implemented for the class of projection selection
functions introduced in the next section.
are not. Thus,
whenever possible, equivalence classes should be defined so as to
account for possibly equivalent compositions of selection functions.
This is easily implemented for the class of projection selection
functions introduced in the next section.
Mathematically definition 1 states that each edge has an
attached observation model via mapping ![]() . Computationally the edge
instead selects (in practice points to) a model application structure
which identifies the observation model and the corresponding selection
function. We denote the set of observation model applications by
. Computationally the edge
instead selects (in practice points to) a model application structure
which identifies the observation model and the corresponding selection
function. We denote the set of observation model applications by
![]() . Inclusion within the recursive hierarchy induces a
partial ordering on this set where it is important to realize that a
given model application may be referenced at more than one recursive
level. We extend this ordering by specifying that all primitive
observation models are dominated by any FGM. In what follows we will
then assume that
. Inclusion within the recursive hierarchy induces a
partial ordering on this set where it is important to realize that a
given model application may be referenced at more than one recursive
level. We extend this ordering by specifying that all primitive
observation models are dominated by any FGM. In what follows we will
then assume that
![]() is indexed in topological order so that
the top-level FGM is first and the primitive models form the list's
end.
is indexed in topological order so that
the top-level FGM is first and the primitive models form the list's
end.
We also introduce choice model application structures
![]() . Since choice models do not depend on
. Since choice models do not depend on ![]() or involve a
selection function, these structures are in 1:1 correspondence with
the choice models themselves and are identically indexed. Many
references may exist to a choice model, and its corresponding
application structure avoids redundant model evaluation by recording
the model's current value. It also accumulates
or involve a
selection function, these structures are in 1:1 correspondence with
the choice models themselves and are identically indexed. Many
references may exist to a choice model, and its corresponding
application structure avoids redundant model evaluation by recording
the model's current value. It also accumulates ![]() contributions
during expectation step processing so that a single call may be made
to maximize the model. This is explained later in greater detail.
contributions
during expectation step processing so that a single call may be made
to maximize the model. This is explained later in greater detail.
If an FGM ![]() is a recursive child of a parent
is a recursive child of a parent ![]() , one
alternative is to eliminate the recursion and expand the child inline within the parent by adding vertices and edges to its DAG.
If
, one
alternative is to eliminate the recursion and expand the child inline within the parent by adding vertices and edges to its DAG.
If ![]() is invoked along edge
is invoked along edge ![]() between vertices
between vertices ![]() and
and ![]() then
the first step of this inline expansion disconnects
then
the first step of this inline expansion disconnects ![]() from
from ![]() and
replaces the invocation of
and
replaces the invocation of ![]() with a void model. The child
with a void model. The child ![]() is
then inserted between the disconnected end and vertex
is
then inserted between the disconnected end and vertex ![]() .
.
When evaluating ![]() this inline expansion clearly isn't necessary
since one can evaluate
this inline expansion clearly isn't necessary
since one can evaluate ![]() in isolation, record its value in
the model application structure, and in constant time refer to that
value where needed in
in isolation, record its value in
the model application structure, and in constant time refer to that
value where needed in ![]() . The same is true for parameter
reestimation although a brief argument is needed.
. The same is true for parameter
reestimation although a brief argument is needed.
proof: Let ![]() connect vertices
connect vertices ![]() and
and ![]() and let
and let ![]() denote some
source-sink path of
denote some
source-sink path of ![]() and
and ![]() its weight.
If
its weight.
If ![]() is expanded inline
the value of
is expanded inline
the value of ![]() will be
will be
![]() .
In isolation it is
.
In isolation it is
![]() .
But
.
But
![]() from which the proposition follows.
from which the proposition follows.![]()
So if the same model application ![]() is pointed to by many FGM
edges, the right computational approach is to first accumulate their
is pointed to by many FGM
edges, the right computational approach is to first accumulate their
![]() values and then to process
values and then to process ![]() . Here we emphasize that
this approach is more efficient and mathematically identical to
inline expansion. So if at the bottom of the recursion the required
. Here we emphasize that
this approach is more efficient and mathematically identical to
inline expansion. So if at the bottom of the recursion the required
![]() problems are solved, then at all higher levels they are too.
problems are solved, then at all higher levels they are too.
An observation model ![]() that is not an FGM is said to be primitive,
and is represented by an abstract type for which the following
operations are defined:
that is not an FGM is said to be primitive,
and is represented by an abstract type for which the following
operations are defined:
Here ![]() is an element of the range of a selection function and
is an element of the range of a selection function and
![]() is a non-negative weight propagated down as described in
proposition 2. The evaluate function returns the value
of
is a non-negative weight propagated down as described in
proposition 2. The evaluate function returns the value
of ![]() at
at ![]() . Notice that the model's parameters
. Notice that the model's parameters ![]() are
hidden by the abstract type. In practice a mutator may be provided
to set them and a selector provided for readout. The names Estep and Mstep follow the EM literature even though FGMs
are not restricted to maximum-likelihood estimation of probability
functions and densities.
are
hidden by the abstract type. In practice a mutator may be provided
to set them and a selector provided for readout. The names Estep and Mstep follow the EM literature even though FGMs
are not restricted to maximum-likelihood estimation of probability
functions and densities.
Given a sequence of values
![]() , and nonnegative multiplicities
, and nonnegative multiplicities
![]() the Estep and Mstep procedures
address the following optimization problem:
the Estep and Mstep procedures
address the following optimization problem:
which generalizes Eq. 5. The Estep
procedure is called for each
![]() and then Mstep is
called to reestimate the model's parameters. For some models the
result is the unique optimum parameter set, but in general the process
is repeated. For example, if the
and then Mstep is
called to reestimate the model's parameters. For some models the
result is the unique optimum parameter set, but in general the process
is repeated. For example, if the ![]() are letters of the alphabet,
the
are letters of the alphabet,
the ![]() are positive frequencies, and the model's value
is a probability for each letter, then Estep need only record the
are positive frequencies, and the model's value
is a probability for each letter, then Estep need only record the
![]() values provided and Mstep can easily determine the
unique optimal model. That is:
values provided and Mstep can easily determine the
unique optimal model. That is:
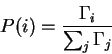
We point out that if the probability of symbol ![]() is zero
prior to reestimation, then
is zero
prior to reestimation, then ![]() and therefore its reestimate
and therefore its reestimate
![]() are zero. Such parameters in this simple discrete model are then
effectively disabled since their corresponding choice of alphabet
symbol will always have probability zero.
are zero. Such parameters in this simple discrete model are then
effectively disabled since their corresponding choice of alphabet
symbol will always have probability zero.
A simple unique solution also exists for the normal density and others. In the discrete example above the model is constrained to produce values which sum to one over the alphabet. Normal densities are constrained to integrate to one. These constraints are obviously important so that the overall optimization problem has a bounded solution. But it is important to observe that their precise nature is irrelevant and invisible to the FGM framework. In particular there is no need for a model to represent a probability function There is also no need to restrict one's attention to models for which unique optimum solutions are readily available. As noted earlier, any progress made for even one model, will translate to progress in the overall FGM optimization.
A choice ![]() is represented by an abstract type for which
the following operations are defined:
is represented by an abstract type for which
the following operations are defined:
Here ![]() is the index of an edge and the evaluate function
returns its value under
is the index of an edge and the evaluate function
returns its value under ![]() given the model's current parameters
given the model's current parameters
![]() . The Mstep procedure is passed the vector
. The Mstep procedure is passed the vector
![]() and addresses the following optimization
problem:
and addresses the following optimization
problem:
If ![]() is a probability function then the problem is
exactly that of Eq. 6 and an exact solution is
available. In both cases the solution is mathematically optimal but
other problem constraints might be incorporated into
is a probability function then the problem is
exactly that of Eq. 6 and an exact solution is
available. In both cases the solution is mathematically optimal but
other problem constraints might be incorporated into ![]() or
or ![]() that sometimes forbid it. For example, one might prohibit
probabilities from falling below some fixed threshold. This amounts
to a change in parameterization and we will see in a later section
that this capability may be used to alter the meaning of optimal
in useful ways. Note that we might instead have
treated a choice model as an observation model over the natural
numbers but decided that their roles are sufficiently distinct to
warrant separate designs.
that sometimes forbid it. For example, one might prohibit
probabilities from falling below some fixed threshold. This amounts
to a change in parameterization and we will see in a later section
that this capability may be used to alter the meaning of optimal
in useful ways. Note that we might instead have
treated a choice model as an observation model over the natural
numbers but decided that their roles are sufficiently distinct to
warrant separate designs.
We now return to our discussion of model applications and begin by
describing the information that must be associated with these
structures. An observation application structure ![]() contains:
contains:
A choice application structure ![]() contains:
contains:
No model variable is needed since indexing corresponds to that of the choice models themselves.
Recall that the mathematical definition 1 of an FGM
associates edges directly with elements of ![]() via functions
via functions
![]() - there are no model application structures. While the FGM
along with its associated model application structure lists might be
generated incrementally, it is simpler to imagine that the FGM is first
specified mathematically and then compiled into a form that
includes these lists. This compiled form is denoted
- there are no model application structures. While the FGM
along with its associated model application structure lists might be
generated incrementally, it is simpler to imagine that the FGM is first
specified mathematically and then compiled into a form that
includes these lists. This compiled form is denoted ![]() and merges
the
and merges
the ![]() sets of each FGM into single densely enumerated sets. In
compiled form FGM edges do not point directly to observation models
but rather to observation model application structures. The
sets of each FGM into single densely enumerated sets. In
compiled form FGM edges do not point directly to observation models
but rather to observation model application structures. The ![]() function is replaced by
function is replaced by ![]() to effect this change.
to effect this change.
We present evaluation, expectation step, and maximization step algorithms for compiled FGMs. These are not recursive functions but rather operate by traversing the global model application lists built during compilation.
Before any of these are called the FGM must be initialized. This
procedure
![]() consists of setting the
consists of setting the
![]() variables to zero in all choice model application structures and
then evaluating each choice model and recording its value there.
variables to zero in all choice model application structures and
then evaluating each choice model and recording its value there.
Evaluating an FGM and performing an expectation step
are carried out by bottom-up (reverse order) and top-down (in order)
traversals respectively of the model application lists.
Evaluation returns a single value for ![]() given observation
given observation ![]() and
also records the value of all subsidiary models within the observation
model application structures.
and
also records the value of all subsidiary models within the observation
model application structures.
where algorithm 1 refers to the appropriate
observation and choice application structure value variables rather
than computing ![]() and
and ![]() .
.
As for primitive observation models the FGM expectation step procedure
accepts a ![]() argument. Supplying a value of
argument. Supplying a value of ![]() for each
for each ![]() observed corresponds to the optimization problem of Eq. 5.
In general these
observed corresponds to the optimization problem of Eq. 5.
In general these ![]() values generalize the problem by appearing
as exponents to the FGM's value as in
values generalize the problem by appearing
as exponents to the FGM's value as in
![]() . The FGM
is first evaluated so that the observation model application
structures contain current values. Their
. The FGM
is first evaluated so that the observation model application
structures contain current values. Their ![]() values are then set
to zero except for the first which corresponds to the top-level FGM
and is set to the function's
values are then set
to zero except for the first which corresponds to the top-level FGM
and is set to the function's ![]() argument. The main loop
proceeds top-down to propagate
argument. The main loop
proceeds top-down to propagate ![]() contributions to lower
observation model application structures. Eventually primitive
structures are reached and a primitive expectation step is performed.
The FGM's value is returned as a convenience since it was necessary
to compute it.
contributions to lower
observation model application structures. Eventually primitive
structures are reached and a primitive expectation step is performed.
The FGM's value is returned as a convenience since it was necessary
to compute it.
The FGM maximization procedure maximizes the primitive observation models and all choice models. The FGM is then reinitialized.
Observe that we do not specify that the models are maximized in any particular order since if their parameter sets are disjoint so is the act of maximizing them. Our notation thus-far has suggested that the parameter sets are in fact independent but in general they need not be. For example, two models might share the same parameters but compute two different functionals depending on them. In this case the two corresponding optimization subproblems of definition 2 are simply combined into one. From an implementation viewpoint this kind of situation can be handled entirely at the model type level through communication between them that is invisible at higher levels. So the fact that algorithm 6 specifies no order for maximization does not imply that we are limited to the case of disjoint parameter sets.
Analysis of the algorithms above is straightforward from the structure of
the compiled FGM ![]() . Let
. Let ![]() denote the sum over nonprimitive
observation model applications, of the number of edges in the FGM
corresponding to each. Then both evaluation and expectation step
processing require
denote the sum over nonprimitive
observation model applications, of the number of edges in the FGM
corresponding to each. Then both evaluation and expectation step
processing require ![]() time where
time where ![]() denotes the time
needed to perform the required primitive observation model type
operations. These are described by the final entries in the list of
observation model applications. When these primitive operations are
denotes the time
needed to perform the required primitive observation model type
operations. These are described by the final entries in the list of
observation model applications. When these primitive operations are
![]() time the overall complexity is just
time the overall complexity is just ![]() since their number
cannot exceed
since their number
cannot exceed ![]() . Each choice model is evaluated once during initialize. The maximize operation time-complexity is just
that required to perform a maximization step for each observation and
choice model in the system. Ignoring the internal requirements of the
observation and choice models, it is obvious that
. Each choice model is evaluated once during initialize. The maximize operation time-complexity is just
that required to perform a maximization step for each observation and
choice model in the system. Ignoring the internal requirements of the
observation and choice models, it is obvious that ![]() requires
requires
![]() space.
space.
The algorithms above are conceptually straightforward, but an
important numerical issue must be faced in their implementation. As
one sweeps through the DAG, the ![]() and
and ![]() variables can
easily become too large or small to represent as conventional floating
point values. This is true even of the final FGM value. If the FGM
is a probability model, exponent-range underflow is the issue and
corresponds to an extremely small probability of generating any
particular observation. For complex problems this behavior is the
rule not the exception since element probabilities in general decline
exponentially with dimension. Logarithmic representation is one
solution but the authors have also explored a floating point
representation with extended exponent range as reported in
[23]. Because
variables can
easily become too large or small to represent as conventional floating
point values. This is true even of the final FGM value. If the FGM
is a probability model, exponent-range underflow is the issue and
corresponds to an extremely small probability of generating any
particular observation. For complex problems this behavior is the
rule not the exception since element probabilities in general decline
exponentially with dimension. Logarithmic representation is one
solution but the authors have also explored a floating point
representation with extended exponent range as reported in
[23]. Because ![]() variables are normalized by
variables are normalized by
![]() they may be adequately represented using standard floating
point.
they may be adequately represented using standard floating
point.
We now briefly discuss the computational complexity of FGM
maximization. A restricted class of FGMs is identified for which
maximization is shown to be NP-complete. Members of this class have
constant choice functions that assume value ![]() . There are two
selection functions
. There are two
selection functions ![]() and
and ![]() that assume constant values
that assume constant values ![]() and
and ![]() respectively. Notice that there is no dependency on any
observation. Each observation model has a single parameter bit
respectively. Notice that there is no dependency on any
observation. Each observation model has a single parameter bit ![]() and given boolean argument
and given boolean argument ![]() assumes value
assumes value
![]() . The FGM then assumes a bounded integral value
and the maximization problem is well-posed. The corresponding
decision problem is: does there exist a set of parameter bits such
that the FGM's value is greater than a given integer
. The FGM then assumes a bounded integral value
and the maximization problem is well-posed. The corresponding
decision problem is: does there exist a set of parameter bits such
that the FGM's value is greater than a given integer ![]() ? This problem
is clearly in NP since given a set of parameter bits, FGM evaluation,
which runs in linear time, may be used to answer the question. We will
refer to this setting as the LFGM (logical FGM) problem.
? This problem
is clearly in NP since given a set of parameter bits, FGM evaluation,
which runs in linear time, may be used to answer the question. We will
refer to this setting as the LFGM (logical FGM) problem.
proof: The NP-complete SAT problem is easily reduced to LFGM by first
associating an observation model with each variable. If the variable
![]() occurs in a clause then selector
occurs in a clause then selector ![]() or
or ![]() is used
respectively. Clauses gives rise to trivial FGMs in which each term
corresponds to a distinct edge from source to sink with the
appropriate observation model and selection function attached. The
FGMs for each clause are then concatenated to form the final FGM. The
set of clauses are then satisfied if and only if the FGM assumes a
value greater than zero. The reduction's complexity is linear whence
LFGM is NP-complete.
is used
respectively. Clauses gives rise to trivial FGMs in which each term
corresponds to a distinct edge from source to sink with the
appropriate observation model and selection function attached. The
FGMs for each clause are then concatenated to form the final FGM. The
set of clauses are then satisfied if and only if the FGM assumes a
value greater than zero. The reduction's complexity is linear whence
LFGM is NP-complete.![]()
It is possible to construct reductions like that above where the observation models are continuous not discrete functions; but further discussion of the complexity of continuous optimization is beyond the scope of this paper. These continuous formulations correspond to stochastic continuous embedding approaches to SAT and represent an interesting area for future work.
This concludes our development of FGMs as general mixture-forms and in
closing we remark that our framework is certainly open to additional
generalization and refinement. For example one might introduce choice
models that also depend on the observation, or replace the ![]() edge association functions with distributions. Many such variations
are possible but our goal was a development somewhere between
empty generalization and over specialization.
edge association functions with distributions. Many such variations
are possible but our goal was a development somewhere between
empty generalization and over specialization.
In this section we consider specializations of Finite Growth Models such that their value represents a probability. The associated DAG and attached models may then be viewed as an acyclic automaton directing the stochastic generation of objects. Stochastic modeling is the original motivation for FGMs and much of our nomenclature is drawn from this viewpoint.
The first step is to specialize the selection functions of definition
1 to projections. That is, functions that select some
subset of the dimensions of tuple observation ![]() . A projection is
characterized by a subset
. A projection is
characterized by a subset ![]() of the dimension indices of
of the dimension indices of ![]() . We
associate some subset
. We
associate some subset ![]() with every edge
with every edge ![]() of the FGM and then
denote by
of the FGM and then
denote by ![]() , the projection of observation tuple
, the projection of observation tuple
![]() corresponding to selection of the components in
corresponding to selection of the components in ![]() . This then
is the selection function associated with
. This then
is the selection function associated with ![]() . For some edge
. For some edge ![]() suppose
suppose ![]() . Then
. Then ![]() is a tuple with two
components which are equal in value to the second and fourth
components of
is a tuple with two
components which are equal in value to the second and fourth
components of ![]() . We assume for now that
. We assume for now that
![]() but
will later see that this is unnecessary. A composition of
projections, applied to
but
will later see that this is unnecessary. A composition of
projections, applied to ![]() , is again a projection characterized by
some dimensional subset; whence it is straightforward to define
equivalence for the purpose of identifying truly distinct model
applications for recursively combined FGMs. The use of projections
corresponds to the generation of observations in arbitrary groupings
and orderings - a fact we will rely on later in our discussion of
stochastic transduction.
, is again a projection characterized by
some dimensional subset; whence it is straightforward to define
equivalence for the purpose of identifying truly distinct model
applications for recursively combined FGMs. The use of projections
corresponds to the generation of observations in arbitrary groupings
and orderings - a fact we will rely on later in our discussion of
stochastic transduction.
Next we assume that all choice and observation models are probability
functions or densities. Each ![]() then corresponds to a stochastic
choice among edges to follow. Each
then corresponds to a stochastic
choice among edges to follow. Each ![]() corresponds to
stochastic generation of some portion of
corresponds to
stochastic generation of some portion of ![]() (since our
selectors are projections).
(since our
selectors are projections).
Finally we specialize the ![]() subsets so that along any source-sink
path their intersection is void and their union is the complete set of
dimensions. Each path then represents one way in which
subsets so that along any source-sink
path their intersection is void and their union is the complete set of
dimensions. Each path then represents one way in which ![]() might be
stochastically generated or grown and corresponds to a permutation
of the dimensional indices
might be
stochastically generated or grown and corresponds to a permutation
of the dimensional indices ![]() . The ``finite growth model''
framework is so named because we imagine that complete observations
are grown, starting from the empty set, in many possible orderings, as
specified by the model's underlying graph. The value of each
source-sink path through the FGM is the probability of following that
path and generating
. The ``finite growth model''
framework is so named because we imagine that complete observations
are grown, starting from the empty set, in many possible orderings, as
specified by the model's underlying graph. The value of each
source-sink path through the FGM is the probability of following that
path and generating ![]() . The FGM's value is then a probability
function
. The FGM's value is then a probability
function ![]() on
on ![]() , i.e. its sum/integral is one.
When it is necessary to make clear that we are referring to an FGM with
the restrictions above, we will use the term stochastic finite growth model
(SFGM).
, i.e. its sum/integral is one.
When it is necessary to make clear that we are referring to an FGM with
the restrictions above, we will use the term stochastic finite growth model
(SFGM).
After algorithm 1 has run, ![]() gives
gives
![]() . However the other
. However the other ![]() values have meaning as
well. In general
values have meaning as
well. In general ![]() is the probability of arriving at
is the probability of arriving at ![]() and observing that part of
and observing that part of ![]() corresponding to the paths
between
corresponding to the paths
between ![]() and the source. Note that because each source-sink
path corresponds to a permutation of the observation tuple, every
path from the source to
and the source. Note that because each source-sink
path corresponds to a permutation of the observation tuple, every
path from the source to ![]() must generate the same observation
components -- possibly however in different orders. Dually,
must generate the same observation
components -- possibly however in different orders. Dually,
![]() is the probability that random operation of the machine
encounters
is the probability that random operation of the machine
encounters ![]() , while at the same time generating those observation
components accounted for by the source to
, while at the same time generating those observation
components accounted for by the source to ![]() paths. Algorithm
1 sums over all paths through the FGM but is easily
modified to find instead a single optimal path. This is referred to
as the Viterbii decode of the FGM and answers the question:
what is the single most likely explanation for the observation?
paths. Algorithm
1 sums over all paths through the FGM but is easily
modified to find instead a single optimal path. This is referred to
as the Viterbii decode of the FGM and answers the question:
what is the single most likely explanation for the observation?
Algorithm 2 also computes ![]() as
as ![]() . In
general
. In
general ![]() is the probability of observing that part of
is the probability of observing that part of ![]() corresponding to the paths between
corresponding to the paths between ![]() and the sink, given passage
through
and the sink, given passage
through ![]() . Dually,
. Dually, ![]() is the probability that
the machine passes through
is the probability that
the machine passes through ![]() and proceeds on to
generate those observation components accounted for by the
and proceeds on to
generate those observation components accounted for by the ![]() to
sink paths. Denoting by
to
sink paths. Denoting by ![]() the part of
the part of ![]() corresponding to paths
from the source to
corresponding to paths
from the source to ![]() , and by
, and by ![]() the part of
the part of ![]() corresponding to
paths from
corresponding to
paths from ![]() to the sink,
to the sink,
![]() and
and
![]() . But
. But
![]() because an SFGM is a
Markov process. So
because an SFGM is a
Markov process. So
![]() , i.e. the
probability of generating
, i.e. the
probability of generating ![]() and passing through
and passing through ![]() .
.
Observe that the meaning of ![]() is not simply a time-reversed
interpretation of
is not simply a time-reversed
interpretation of ![]() . This is because an SFGM has an intrinsic
directionality. In-bound DAG edge probabilities need not sum to one
so simply reversing edge direction does not leave a well-formed SFGM.
. This is because an SFGM has an intrinsic
directionality. In-bound DAG edge probabilities need not sum to one
so simply reversing edge direction does not leave a well-formed SFGM.
For SFGMs the ![]() values computed by algorithm 3 are
the probabilities
values computed by algorithm 3 are
the probabilities
![]() ; where `
; where `![]() '
refers to the event of a transition over edge
'
refers to the event of a transition over edge ![]() . That is,
. That is,
![]() gives the a posteriori probability of following edge
gives the a posteriori probability of following edge
![]() conditioned on observation (generation) of
conditioned on observation (generation) of ![]() .
Given an SFGM and any
.
Given an SFGM and any ![]() , the
, the ![]() values must satisfy the following
constraint which can in practice be used as an implementation self-check.
It is a specialization of proposition 1 to SFGMs:
values must satisfy the following
constraint which can in practice be used as an implementation self-check.
It is a specialization of proposition 1 to SFGMs:
proof: The key idea is that the edges that observe a given observation dimension
induce a cut in the DAG but we present the proof from a probabilistic viewpoint.
Assume
![]() . Because every source sink path path
generates each observation component exactly once, the set of edges
. Because every source sink path path
generates each observation component exactly once, the set of edges
![]() which generate a particular component
which generate a particular component ![]() , corresponds to a set
of mutually exclusive and exhaustive events. Hence
, corresponds to a set
of mutually exclusive and exhaustive events. Hence
![]() . There are
. There are ![]() observation
components, and these partition
observation
components, and these partition ![]() into disjoint sets
into disjoint sets ![]() . So
. So
![]() , establishing the first part of the
proposition. In general, the
, establishing the first part of the
proposition. In general, the ![]() are not disjoint, and the number of
sets to which an edge
are not disjoint, and the number of
sets to which an edge ![]() belongs is
belongs is ![]() . Multiplying each
. Multiplying each
![]() by
by ![]() in effect gives each set its own copy, so
that the sum remains
in effect gives each set its own copy, so
that the sum remains ![]() .
. ![]()
We required above that
![]() . If necessary this
restriction may be effectively removed and one may include so called
nonemitting edges in a model. To do so the observation tuple
is augmented with dummy components each capable of assuming only
a single value. Nonemitting edges then observe these components
assigning them probability one. The result is a probability model on
the augmented observation space, and since its extension was trivial,
on the original space.
. If necessary this
restriction may be effectively removed and one may include so called
nonemitting edges in a model. To do so the observation tuple
is augmented with dummy components each capable of assuming only
a single value. Nonemitting edges then observe these components
assigning them probability one. The result is a probability model on
the augmented observation space, and since its extension was trivial,
on the original space.
The ![]() and
and ![]() functions of our FGM framework may be used to implement the
parameter tying concept from the stochastic modeling literature.
When
functions of our FGM framework may be used to implement the
parameter tying concept from the stochastic modeling literature.
When
![]() the observation models attached to these edges
are said to be tied. If the edges leaving vertex
the observation models attached to these edges
are said to be tied. If the edges leaving vertex ![]() map under
map under ![]() to the same choice model as those leaving another vertex
to the same choice model as those leaving another vertex ![]() , the
choice models at
, the
choice models at ![]() and
and ![]() are said to be tied. In crafting a
model there are two reasons for parameter tying. The first is that it
reduces the number of free parameters in the model and as such combats
overtraining. The second is that problem domain knowledge may suggest
that two models represent the same underlying phenomenon.
are said to be tied. In crafting a
model there are two reasons for parameter tying. The first is that it
reduces the number of free parameters in the model and as such combats
overtraining. The second is that problem domain knowledge may suggest
that two models represent the same underlying phenomenon.
Equation 5 formalizes the problem of parameter
optimization given a training set
![]() by forming a
cascade of identical FGMs. More generally we may write:
by forming a
cascade of identical FGMs. More generally we may write:
where now a possibly different FGM is associated with each
training observation but all are tied to a single underlying
collection of choice and observation models. This is an important
conceptual point since it represents the technique used to deal with
training examples of varying dimension. For example, each ![]() might
represent a finite time series. Typically the FGMs are instances of a
single design - varied in order to accommodate the structure of the
observation tuple. Equivalently the entire cascade may be regarded as
a single FGM operating on a single observation formed by concatenation
of the entire training set. This cascading and concatenation is of
conceptual value only. In practice one merely performs expectation
steps for each pair
might
represent a finite time series. Typically the FGMs are instances of a
single design - varied in order to accommodate the structure of the
observation tuple. Equivalently the entire cascade may be regarded as
a single FGM operating on a single observation formed by concatenation
of the entire training set. This cascading and concatenation is of
conceptual value only. In practice one merely performs expectation
steps for each pair ![]() followed by a maximization step.
There is no need to actually form the cascade and concatenation. In
an SFGM setting Eq. 8 represents the training set's
likelihood and our goal of maximizing it corresponds to maximum-likelihood parameter estimation of statistics.
followed by a maximization step.
There is no need to actually form the cascade and concatenation. In
an SFGM setting Eq. 8 represents the training set's
likelihood and our goal of maximizing it corresponds to maximum-likelihood parameter estimation of statistics.
Ultimately one is faced with the task of maximizing primitive models. For simple discrete models and many continuous ones (notably normal densities) each independent maximization problem arising from theorem 1 has a unique globally optimal solution and satisfies certain other conditions. Lemma 1 and theorem 1 may then be strengthened to say that strict progress is made unless one is already at a critical point in parameter space. Even this does not imply parametric convergence however. See [3,11,22] for discussion of the convergence and other properties of the EM algorithm. These mathematical issues including rate of convergence, while important, are not our focus and we will not consider them further. Clearly relating various conditions on primitive models to the resulting behavior of the overall FGM represents an important area for future work.
We saw in the last section that simple discrete models are easily
maximized. If ![]() is a multivariate normal density then
maximization is also easily accomplished since the weighted sample
mean and weighted sample covariance define the maximum-likelihood
parameter set. The weights are
is a multivariate normal density then
maximization is also easily accomplished since the weighted sample
mean and weighted sample covariance define the maximum-likelihood
parameter set. The weights are
![]() where
where ![]() denotes the sum of all
denotes the sum of all ![]() associated with
associated with ![]() . In general,
any density for which a maximum-likelihood estimate is readily
available may be used as an observation model, e.g. beta densities for
random variables confined to
. In general,
any density for which a maximum-likelihood estimate is readily
available may be used as an observation model, e.g. beta densities for
random variables confined to ![]() . See [14] for a
treatment of HMMs including a compact discussion of the discrete and
continuous optimization problems discussed above.
. See [14] for a
treatment of HMMs including a compact discussion of the discrete and
continuous optimization problems discussed above.
SFGMs as defined in the previous section are probability functions on an associated finite dimensional observation space. They arise by restricting the FGM framework in several ways. We now relax certain of these restrictions and show that FGMs may be applied to a much broader class of stochastic modeling problems and settings.
In contrast to an SFGM, stochastic models are frequently defined as either infinite generative processes, or processes that generate finite objects of unbounded size. Time series methods such as hidden Markov models are an example of the first kind and stochastic context free grammars are an example of the second. In the first case the probability of a finite object refers to the aggregated probability of all infinite objects that include it - in the case of strings the combined probability of all infinite strings with a particular finite prefix.
Processes such as these have an associated infinitely deep finite branching structure which is conceptually truncated to a finite DAG that explains observations of some fixed length. This DAG is regarded as part of an FGM whose primitive parameterized models correspond to those of the original process. Given a set of finite observations, a set of corresponding FGMs is constructed as discussed in earlier sections. In this way the parameters of an infinite process that best explain a set of finite observations may be learned using FGMs.
This truncation is conveniently effected within the SFGM framework through the introduction of null observation models. These are simply functionals that assume the value zero everywhere and as such lie trivially within the FGM framework. When generation via the original infinite branching process would result in an observation component beyond the finite set of interest, a void model is attached to that edge and it is redirected to the FGM's sink. In this way the processes infinite graph becomes a finite DAG with a single source and sink. This is illustrated by our discussion of stochastic transducers and hidden Markov models in later sections.
A more subtle issue is addressed by the introduction of void
choice models which assume value ![]() for each outgoing edge. They
are useful when the events associated with future generation may be
partitioned into mutually exclusive sets. Our discussion of stochastic
context free grammars in a later section provides illustration.
for each outgoing edge. They
are useful when the events associated with future generation may be
partitioned into mutually exclusive sets. Our discussion of stochastic
context free grammars in a later section provides illustration.
Maximum likelihood (ML) parameter estimation is a best-fit strategy and is therefore susceptible to overtraining. For example, if a discrete model never observes a given symbol, its ML parameters assign the symbol probability zero. The result can be poor generalization. Also, our discussion thus far has tacitly assumed that a single stochastic model represented as an FGM is used to explain a set of observations. Here too if this model is very complex in comparison to the available training data, generalization will suffer. The model selection problem consists of somehow choosing or forming a model of appropriate complexity.
These two issues are highly related and we will now briefly describe how both may addressed within the FGM framework. The result is a conceptually clear and computationally tractable approach to implementing more sophisticated estimation schemes for both existing and new stochastic models. That EM could accomplish this in general was observed in [11] but does not appear to have impacted the use of EM in practice. We consider two approaches: maximum a posteriori parameter (MAP) estimation, and minimum description length (MDL). Our discussion begins with MAP.
Earlier sections have shown that Baum-Welch/EM may be used to address
the problem of finding ![]() that maximizes
that maximizes ![]() . The form of
this objective corresponds to maximum-likelihood estimation but we
will see that it actually not so limited. Given a prior
. The form of
this objective corresponds to maximum-likelihood estimation but we
will see that it actually not so limited. Given a prior ![]() on
model parameters the MAP objective is to instead maximize
on
model parameters the MAP objective is to instead maximize ![]() .
From the Bayes' rule it follows that this is the same as maximizing
.
From the Bayes' rule it follows that this is the same as maximizing
![]() since this quantity is proportional to
since this quantity is proportional to
![]() , i.e. the denominator is fixed. We resolve
, i.e. the denominator is fixed. We resolve ![]() into
its constituent parts
into
its constituent parts ![]() and
and
![]() corresponding
to the FGM's observation and choice models respectively, and define the
overall prior based on independent parts:
corresponding
to the FGM's observation and choice models respectively, and define the
overall prior based on independent parts:
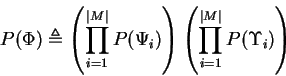
This product may itself be regarded as a linear FGM denoted ![]() with
null observation models, and 1-way choice models having values
corresponding to each product term. Alternatively each term may be
represented as an observation model that assumes a constant value for
each setting of its parameters. The two FGMs
with
null observation models, and 1-way choice models having values
corresponding to each product term. Alternatively each term may be
represented as an observation model that assumes a constant value for
each setting of its parameters. The two FGMs ![]() and
and ![]() are then
combined end-to-end, or in the case of multiple observations
are then
combined end-to-end, or in the case of multiple observations ![]() is
attached to the end of
is
attached to the end of
![]() . The FGM
. The FGM ![]() computes
computes
![]() and
and ![]() computes
computes ![]() so that the cascade thus
formed has value
so that the cascade thus
formed has value
![]() . Maximizing it will then
effect MAP-guided learning.
. Maximizing it will then
effect MAP-guided learning.
The minimum description length principle states that one should choose
a model and its parameters such that the combined cost of describing these followed by the encoded observations is
minimized. The related notion of Kolmogorov complexity deals with the
smallest such description and is generally not computationally
tractable. By contrast MDL practitioners are content to fix some
parameterized scheme of representation and optimize the parameters.
This does not fully implement the MDL principle but captures the
important tension that must exist between model and data complexity.
The cost of describing the observations is
![]() bits
where it is assumed that
bits
where it is assumed that ![]() is a probability function. The cost of
describing the model's structure is upper bounded by choosing some
reasonable representation and counting its bits. The cost of
describing a real valued parameter may be upper bounded by choosing
some number of quantization levels
is a probability function. The cost of
describing the model's structure is upper bounded by choosing some
reasonable representation and counting its bits. The cost of
describing a real valued parameter may be upper bounded by choosing
some number of quantization levels ![]() , assuming uniform quantization (typically),
and describing
, assuming uniform quantization (typically),
and describing ![]() bits per parameter. Many variations are
possible. The final codelength is denoted
bits per parameter. Many variations are
possible. The final codelength is denoted ![]() and the total
description length is
and the total
description length is
![]() . As in the case
of MAP above we assume that
. As in the case
of MAP above we assume that ![]() is formed by summing separate
contributions from primitive models. As before these may be regarded
as a linear FGM where the value of the attached models is just the
corresponding codelength exponentiated. Notice that the
the MDL and MAP constructions are essentially identical and for this
reason we view MDL as a Bayesian approach in which the prior is not
necessarily a probability model.
is formed by summing separate
contributions from primitive models. As before these may be regarded
as a linear FGM where the value of the attached models is just the
corresponding codelength exponentiated. Notice that the
the MDL and MAP constructions are essentially identical and for this
reason we view MDL as a Bayesian approach in which the prior is not
necessarily a probability model.
The important message is that the original maximization problem may be decomposed into separate primitive problems even when the guiding criterion is not maximum-likelihood. Any primitive model for which maximization may be conveniently performed subject to the selected criterion, may be used.
Since the basic FGM is fixed in the discussion above, the cost of describing its representation in the MDL framework is also fixed with respect to FGM maximization. However an important part of the MDL outlook is selecting a model of appropriate complexity. This tension is captured in the FGM framework by forming a finite mixture of models over a range of complexities. Each model is made up of a basic FGM augmented with an MDL extension as described above. The cost of describing the model's design now enters the optimization problem since it differs across mixture components. Rather than selecting a single model complexity, reestimation will learn a distribution on complexity. Each mixture component is the a posteriori probability of its corresponding complexity given the observations. Similarly the MAP setting above may be extended to include the learning of a distribution on model complexity. The model with maximum a posteriori probability may be selected if it is important to identify a single best model. Finally, in the case of MDL the pedantic implementor will account for the complexity of the initial mixture in the overall optimization.
The result is not MDL at all in its original sense since a single model and parameter set is not selected. It is more properly regarded as MAP with MDL-inspired priors.
Our discussion above started by placing all penalty terms together at the front of an FGM. In the model selection example, however, some were placed instead following an initial choice. This may be seen as a special case of a general strategy in which penalty terms are placed as deep as possible within the DAG. That is, just before their first use.
Our discussion has then established:
The practical significance of this theorem is Baum-Welch/EM may be used to efficiently implement estimation criteria more sophisticated than ML with which it is historically associated - and via FGMs it is clear how this can be done for a wide variety of models.
The trivial discrete probability model on an alphabet of ![]() members
has
members
has ![]() nonnegative free parameters that sum to at most unity. Many
other possibilities exist. For example, if alphabet symbols
correspond to states in a truncated Poisson process then the Poisson
probability function
nonnegative free parameters that sum to at most unity. Many
other possibilities exist. For example, if alphabet symbols
correspond to states in a truncated Poisson process then the Poisson
probability function ![]() may be used. This is true of a
choice model as well and has application in the modeling of event
durations. In general we remark that the use of nontrivially
parameterized choice functions represents an interesting direction
that has received only limited attention.
may be used. This is true of a
choice model as well and has application in the modeling of event
durations. In general we remark that the use of nontrivially
parameterized choice functions represents an interesting direction
that has received only limited attention.
In our SFGM framework each edge generates some subset of the observation tuple's components such that as one moves from source to sink each is generated once. The values generated depend only on the edge over which generation is transiting. This corresponds to the first-order Markov assumption of stochastic modeling. In particular the value cannot depend upon route followed to reach the edge. But dependence on observation components generated earlier along the path does not violate the Markov assumption. Formally the observation models are then conditional probability functions where the conditioning is on earlier observation components - not earlier edge sequences. Each source-sink path then corresponds to a causal chain of conditional probabilities so that the FGM's value is a probability.
Brown observes in his thesis [7] that the HMM output independence assumption may be relaxed to allow generation of the current speech sample window to depend on the previous one. He then uses Baum-Welch reestimation without reproof. His focus is on minimizing the number of model parameters - and we suspect that it is only for this reason that he did not propose longer context dependencies.
Our contribution is then the formalization of this message in general form within the FGM framework. That is: the problem of optimizing FGMs that employ conditional observation models is reduced to corresponding primitive conditional maximization problems.
Given a ![]() pixel real-valued image one may model each pixel
position as a function of some surrounding context. If each model's value
is a probability and the context-induced dependency graph has no
cycles, then the individual pixel probabilities may be multiplied to
result in a causal probability model.
Causal models are commonly built by fixing a scanning sequence and
choosing contexts with respect to the implied temporal ordering.
Since there is frequently no single natural scanning sequence the causality
restriction may limit model effectiveness by preventing all of a pixel's
neighbors from contributing to its prediction.
pixel real-valued image one may model each pixel
position as a function of some surrounding context. If each model's value
is a probability and the context-induced dependency graph has no
cycles, then the individual pixel probabilities may be multiplied to
result in a causal probability model.
Causal models are commonly built by fixing a scanning sequence and
choosing contexts with respect to the implied temporal ordering.
Since there is frequently no single natural scanning sequence the causality
restriction may limit model effectiveness by preventing all of a pixel's
neighbors from contributing to its prediction.
If the causality restriction is discarded each pixel's model is strengthened but their product is no longer a probability. This corresponds to relaxing the requirement that the projection functions in an SFGM correspond to a permutation of the observation dimensions. Noncausal neighborhood systems have proven useful in image processing [8].
Since reestimation must nevertheless climb we have the result that even a noncausal unnormalized models like that sketched above may be improved within the FGM framework.
As remarked earlier we might have allowed choice functions to depend on
the observation ![]() . Given choices
. Given choices
![]() the FGM may then
follow each with probability
the FGM may then
follow each with probability ![]() . In contrast with the conventional
static notion of state transition probability, such choice models are
dynamic - responding to the observation. This provides interesting new
modeling flexibility.
If the portion of
. In contrast with the conventional
static notion of state transition probability, such choice models are
dynamic - responding to the observation. This provides interesting new
modeling flexibility.
If the portion of ![]() used to influence the choice is generated earlier
in the DAG (closer to the sink), then one can build probability models
using dynamic choices. We remark, however, that useful models may exist
that violate this assumption and therefore generate values that without
normalization do not represent probabilities.
used to influence the choice is generated earlier
in the DAG (closer to the sink), then one can build probability models
using dynamic choices. We remark, however, that useful models may exist
that violate this assumption and therefore generate values that without
normalization do not represent probabilities.
The notion of transduction has its roots in classical formal language theory (e.g. [6]) and represents the formalization of the idea of a machine that converts an input sequence into an output sequence. Later work within the syntactic pattern recognition outlook addressed the induction problem for a particular subclass of finite transducer [19]. More recently a stochastic approach was taken in [4] where hidden Markov models were used to capture an input-output relationship between synchronous time series.
Finite growth models can be used to derive Baum-Welch/EM based learning algorithms for stochastic transducers. This interesting class of stochastic models capture in a somewhat general way the relationship between dependent symbol streams. In particular there is no assumption that the streams are synchronous, and the symbols singly or jointly generated during transduction can depend upon all context information, i.e. that in every series involved.
Many problems of pattern recognition and artificial intelligence such as speech or handwriting recognition may be viewed as transductions from an input signal to an output stream of discrete symbols - perhaps via one or more intermediate languages. In this conceptual framework it is interesting to note that speech synthesis is merely transduction in the reverse direction. In this section we first discuss transduction in general terms, and then focus in detail on the simple memoryless transducer that corresponds to the widely-used notion of string edit distance.
Given observed strings
![]() the transducer
the transducer ![]() assigns
a probability
assigns
a probability ![]() which represents the sum over generation
sequences that generate
which represents the sum over generation
sequences that generate ![]() , of the probability of each. The FGM
formalism provides a natural way to understand and reason about this
complicated process and we now describe the reduction of a stochastic
transducer and associated finite observation to an FGM.
, of the probability of each. The FGM
formalism provides a natural way to understand and reason about this
complicated process and we now describe the reduction of a stochastic
transducer and associated finite observation to an FGM.
Denoting the states of ![]() by
by ![]() the transducer's infinitely
deep temporal branching structure is truncated to form an FGM with
states
the transducer's infinitely
deep temporal branching structure is truncated to form an FGM with
states
![]() where each
where each ![]() is a
nonnegative integer and
is a
nonnegative integer and
![]() is the source. The
superscript indices correspond to the number of symbols that have been
written to the transducer's
is the source. The
superscript indices correspond to the number of symbols that have been
written to the transducer's ![]() output tapes.
output tapes.
The FGM contains another set of states
![]() defined similarly except that the
subscript refers to a pair of states in the original automaton. Edges
exist between these two state sets but not between members of each.
There are edges leaving each state
defined similarly except that the
subscript refers to a pair of states in the original automaton. Edges
exist between these two state sets but not between members of each.
There are edges leaving each state
![]() leading to
leading to
![]() . Row
. Row ![]() of stochastic transition matrix
of stochastic transition matrix ![]() provides the corresponding choice
model where the matrix entries are the parameters. The observation
model attached to each such edge assumes the constant value
provides the corresponding choice
model where the matrix entries are the parameters. The observation
model attached to each such edge assumes the constant value ![]() .
.
Directed edges exist between ![]() states and
states and ![]() states reflecting the
writing of
states reflecting the
writing of ![]() -tuples to the output tape. For each transition
-tuples to the output tape. For each transition ![]() from state
from state ![]() to
to ![]() in the original automaton, several FGM edges
may be required because the function
in the original automaton, several FGM edges
may be required because the function ![]() may generate output of
differing lengths. More formally for all
may generate output of
differing lengths. More formally for all
![]() an edge exists leaving
an edge exists leaving
![]() leading to
leading to
![]() . Each such edge generates
observations according to
. Each such edge generates
observations according to ![]() , but only string tuples with lengths
, but only string tuples with lengths
![]() are allowed. Void choice models are used
for all edges from
are allowed. Void choice models are used
for all edges from ![]() to
to ![]() .
.
Finally positions in the string-tuple observation are
enumerated and appropriate projectors serve as the FGMs selection
functions and associate observation models with the generation
particular positions in the output tape. Notice that along a
source-sink path the corresponding projections are disjoint and do
cover all positions but do not in general do so in a simple left-right
fashion. This completes our reduction of ![]() to an FGM.
to an FGM.
We now evaluate the complexity of FGM operations by counting edges.
In general each function ![]() may generate output tuples of unbounded
total length. But in some cases such as that of string edit distance
discussed shortly, the length of the string generated in each tuple
position is bounded by some value
may generate output tuples of unbounded
total length. But in some cases such as that of string edit distance
discussed shortly, the length of the string generated in each tuple
position is bounded by some value ![]() .
.
If ![]() denotes the length of the longest string in the observation
tuple, the FGM has
denotes the length of the longest string in the observation
tuple, the FGM has ![]() states
states
![]() and
there are
and
there are ![]() edges leaving each of them leading to
edges leaving each of them leading to
![]() states. The
states. The ![]() states number
states number ![]() .
The out-degree of a
.
The out-degree of a ![]() state is clearly
state is clearly ![]() making the total number of
edges
making the total number of
edges
![]() and this gives the time and space complexity of
FGM operations assuming constant time for primitive model operations.
The out-degree of a
and this gives the time and space complexity of
FGM operations assuming constant time for primitive model operations.
The out-degree of a ![]() state is at most
state is at most ![]() in the FGM so an alternative
expression
in the FGM so an alternative
expression
![]() applies even when
applies even when ![]() has infinite support.
has infinite support.
Having reduced ![]() to an FGM we identify several important operations
and briefly describe their corresponding FGM computation:
to an FGM we identify several important operations
and briefly describe their corresponding FGM computation:
A cascade operation may also be defined where the output of one transducer becomes the input to another. The development above has then established
Note that the space complexity of evaluation and decode is actually smaller since only a forward pass is performed and there is no need to maintain a fully formed DAG in memory. Also, our earlier comments regarding alternative maximization criteria apply to transducers as well and other generalizations are possible including multiple start states and parameter tying.
The edit distance between two finite strings
![]() over finite alphabet
over finite alphabet ![]() is the least costly way to
transform
is the least costly way to
transform ![]() into
into ![]() via single-symbol insertions, deletions, and
substitutions. The non-negative costs of these primitive edit
operations are parameters to the algorithm. These costs
are represented as a table
via single-symbol insertions, deletions, and
substitutions. The non-negative costs of these primitive edit
operations are parameters to the algorithm. These costs
are represented as a table
![]() of size
of size
![]() , where row and column
, where row and column
![]() correspond to an additional alphabet member
correspond to an additional alphabet member ![]() representing the null character. See
[26] for review or [12] for a compact discussion.
The entry in table position
representing the null character. See
[26] for review or [12] for a compact discussion.
The entry in table position ![]() gives the cost of substituting symbol
gives the cost of substituting symbol ![]() of
of ![]() for symbol
for symbol ![]() of
of ![]() . The
first row gives insertion costs, the first column gives deletion
costs, and the remaining entries specify substitution costs. The
table need not be symmetric. Recall that a simple dynamic program
finds the edit distance in
. The
first row gives insertion costs, the first column gives deletion
costs, and the remaining entries specify substitution costs. The
table need not be symmetric. Recall that a simple dynamic program
finds the edit distance in
![]() time.
time.
The task of learning an optimal cost table is clearly
under-constrained, because the string edit distance for all strings
may be trivially minimized by setting all edit costs to zero. Our
outlook is stochastic and we therefore interpret each cost as
![]() of the corresponding event probability. For example, an
entry in the top row expresses the probability of choosing to insert a
particular symbol into the left string. The natural constraint then
requires that the probabilities that underly the cost table must sum
to one. Expressed in terms of costs
of the corresponding event probability. For example, an
entry in the top row expresses the probability of choosing to insert a
particular symbol into the left string. The natural constraint then
requires that the probabilities that underly the cost table must sum
to one. Expressed in terms of costs ![]() , this translates to:
, this translates to:
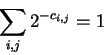
Rather than imagining an editing process that transforms ![]() into
into ![]() ,
we equivalently imagine that the pair
,
we equivalently imagine that the pair ![]() is grown in a
series of steps of three kinds: joint steps, left steps, and right
steps. This outlook was first introduced in section 3.2.2 of
[12]. Our contribution is its further development to include
the learning of costs and the construction of more sophisticated
distance functions as described later in this section. In [24]
the authors implement the learning of costs and give experimental results.
is grown in a
series of steps of three kinds: joint steps, left steps, and right
steps. This outlook was first introduced in section 3.2.2 of
[12]. Our contribution is its further development to include
the learning of costs and the construction of more sophisticated
distance functions as described later in this section. In [24]
the authors implement the learning of costs and give experimental results.
The process is formally a 2-way stochastic transducer with a single
state, no memory, and ![]() . The initial state of the process is
. The initial state of the process is
![]() . A joint step concatenates symbols to both
elements of the pair. A right step adds a symbol to only the right
element of the pair, while a left step adds a symbol to the left
element. In the language of string edit distance, a joint step
corresponds to a substitution operation. When a joint step adds the
same symbol to both strings, one is substituting a symbol for itself.
A right step corresponds to an insertion operation, and a left step
corresponds to a deletion operation.
. A joint step concatenates symbols to both
elements of the pair. A right step adds a symbol to only the right
element of the pair, while a left step adds a symbol to the left
element. In the language of string edit distance, a joint step
corresponds to a substitution operation. When a joint step adds the
same symbol to both strings, one is substituting a symbol for itself.
A right step corresponds to an insertion operation, and a left step
corresponds to a deletion operation.
Figure 1 depicts the table now denoted ![]() after conversion to probabilities. The zero entries correspond to
infinite costs. The stochastic choice between left, right, and joint
generation is implicit in this table. That is,
after conversion to probabilities. The zero entries correspond to
infinite costs. The stochastic choice between left, right, and joint
generation is implicit in this table. That is, ![]() combines choice
and observation probabilities. For example, the sum of the top row
may be interpreted as the probability of choosing to perform a left
insertion.
combines choice
and observation probabilities. For example, the sum of the top row
may be interpreted as the probability of choosing to perform a left
insertion.
Figure 2 depicts the FGM corresponding to stochastic
edit distance between strings of length ![]() and
and ![]() . Its 3-way
branching pattern follows from the structure of the corresponding growth
process and matches exactly the dependency structure of the dynamic
program for conventional edit distance.
. Its 3-way
branching pattern follows from the structure of the corresponding growth
process and matches exactly the dependency structure of the dynamic
program for conventional edit distance.
Notice that all but the sink and the bottom and rightmost vertices
have ternary out-degree, and that the edges leaving them are drawn with
solid lines. These are all in tied. Both their choice and
observation models are specified by ![]() corresponding to normal
operation of the generative stochastic process. Edges drawn with
dotted lines implement truncation of the process and employ null
models. These might have been depicted instead as individual long
edges directly to the sink.
corresponding to normal
operation of the generative stochastic process. Edges drawn with
dotted lines implement truncation of the process and employ null
models. These might have been depicted instead as individual long
edges directly to the sink.
The ![]() operation converts the probability to a non-negative
``distance'', which we will later see corresponds closely to the
standard notion of edit distance. Also notice that in the definition,
we refer to the probability of the ordered pair
operation converts the probability to a non-negative
``distance'', which we will later see corresponds closely to the
standard notion of edit distance. Also notice that in the definition,
we refer to the probability of the ordered pair ![]() . This is an
important distinction since
. This is an
important distinction since ![]() need not be symmetric, and it might
be that
need not be symmetric, and it might
be that
![]() .
.
It is also possible to interpret ![]() with respect to
finite event spaces. If we denote by
with respect to
finite event spaces. If we denote by ![]() the FGM state
corresponding to the argument string lengths, then the probability
defined above may be written:
the FGM state
corresponding to the argument string lengths, then the probability
defined above may be written:
![]() . That is,
the probability of generating
. That is,
the probability of generating ![]() and
and ![]() while passing through
FGM vertex with coordinates
while passing through
FGM vertex with coordinates ![]() . It is straightforward to
compute the probability of event
. It is straightforward to
compute the probability of event
![]() . Division then
yields the conditional probability
. Division then
yields the conditional probability
![]() which
amounts to conditioning on string lengths.
It is also possible to define the FGM differently in order to directly
implement conditioning on string lengths [24].
which
amounts to conditioning on string lengths.
It is also possible to define the FGM differently in order to directly
implement conditioning on string lengths [24].
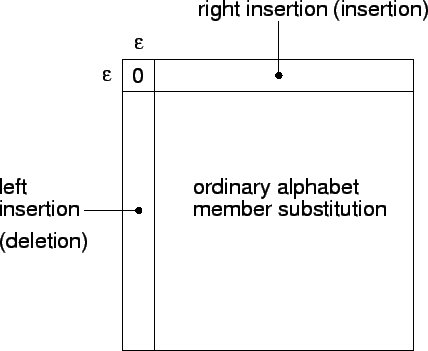
|
The stochastic edit distance
![]() is highly
related but not identical to conventional edit distance. If
stochastic table
is highly
related but not identical to conventional edit distance. If
stochastic table ![]() is converted by
is converted by ![]() to a table of
non-negative costs then conventional edit distance corresponds to the
log-probability of the single best path through the FGM - i.e.
the Viterbi decode.
Stochastic edit distance is the sum over all paths. Basing
decisions on the Viterbi decode is analogous to focusing on the mode
of a distribution while stochastic edit distance corresponds to the mean.
In classification systems we expect that both forms will lead to
nearly identical decisions.
The improved costs we learn in the next
section will provably reduce stochastic edit distances, but we also
expect that in practice they will also improve results for the conventional
form.
to a table of
non-negative costs then conventional edit distance corresponds to the
log-probability of the single best path through the FGM - i.e.
the Viterbi decode.
Stochastic edit distance is the sum over all paths. Basing
decisions on the Viterbi decode is analogous to focusing on the mode
of a distribution while stochastic edit distance corresponds to the mean.
In classification systems we expect that both forms will lead to
nearly identical decisions.
The improved costs we learn in the next
section will provably reduce stochastic edit distances, but we also
expect that in practice they will also improve results for the conventional
form.
We formalize the application of FGMs to stochastic edit distance with the following:
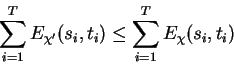
where the inequality is strict unless ![]() is already a critical point.
is already a critical point.
proof: Apply theorem 4.![]()
The FGM formalism is useful to arrive at a correct solution but
because of the extensive parameter tying employed in our construction,
the associated computations may be greatly simplified. There is no
need to build actual DAGs during the computation. Also, as remarked
earlier, the choice model is implicit in ![]() so that creation of
separate choice and observation models is unnecessary when computing
so that creation of
separate choice and observation models is unnecessary when computing
![]() . The probability of passing over an edge is just the
corresponding entry in
. The probability of passing over an edge is just the
corresponding entry in ![]() .
.
The result is algorithm 7. It requires an
![]() array of
array of ![]() values. We write
values. We write ![]() to denote an
element, where
to denote an
element, where
![]() and
and ![]() is
is ![]() or
or ![]() . This
array corresponds to the vertices within two adjacent columns of the
FGM as depicted in figure 2. The logarithm
. This
array corresponds to the vertices within two adjacent columns of the
FGM as depicted in figure 2. The logarithm ![]() of
the joint probability of
of
the joint probability of ![]() and
and ![]() is returned rather than the
probability itself, so that the caller need not deal with extended
range floating point values. As observed by [12], the
algorithm's structure resembles that of the standard dynamic program
for edit distance.
is returned rather than the
probability itself, so that the caller need not deal with extended
range floating point values. As observed by [12], the
algorithm's structure resembles that of the standard dynamic program
for edit distance.
As in the case of evaluation, there is no need to create separate
choice and observation models when implementing reestimation. A brief
argument establishes this fact. Assume we do have separate models.
Then each edge ![]() is of type left, right, or joint,
and during Baum-Welch/EM the quantity
is of type left, right, or joint,
and during Baum-Welch/EM the quantity ![]() will be added to a
choice accumulator and also to an accumulator corresponding to the
observed alphabet symbol or symbols. So the total
will be added to a
choice accumulator and also to an accumulator corresponding to the
observed alphabet symbol or symbols. So the total ![]() contribution to each of the three choice accumulators will exactly
match the contribution to its corresponding observation model. Hence,
if we instead add the
contribution to each of the three choice accumulators will exactly
match the contribution to its corresponding observation model. Hence,
if we instead add the ![]() values directly into an initially zero
array
values directly into an initially zero
array
![]() , the total contributions to the left column, top row,
and interior will exactly correspond to the choice accumulator
contributions above. So after normalization,
, the total contributions to the left column, top row,
and interior will exactly correspond to the choice accumulator
contributions above. So after normalization,
![]() will
represent the same model as that resulting from reestimation based on
separate models.
will
represent the same model as that resulting from reestimation based on
separate models.
Algorithm 8 is the central routine in the stochastic edit
distance learning process. It is called repeatedly with pairs of
strings. The current cost table ![]() must be initialized before the
first call and the improved cost table
must be initialized before the
first call and the improved cost table
![]() must be set to zeros.
As each pair is processed, non-negative values are added to locations
within
must be set to zeros.
As each pair is processed, non-negative values are added to locations
within
![]() . After all the pairs have been presented the
. After all the pairs have been presented the
![]() array is simply normalized so that the sum of its entries is one, and
then represents the set of improved costs. This entire is
repeated to further improve the model. That is,
array is simply normalized so that the sum of its entries is one, and
then represents the set of improved costs. This entire is
repeated to further improve the model. That is,
![]() is copied to
is copied to
![]() and
and
![]() is again set to zeros. The sequence of training pairs
is then presented again, and so on.
is again set to zeros. The sequence of training pairs
is then presented again, and so on.
The algorithm uses two work arrays, ![]() and
and ![]() ,
corresponding to the algorithms 1 and 2
respectively. It is assumed that these arrays are large enough to
accommodate the training pairs. They need not be initialized by the
caller. As in algorithm 7 it is possible to reduce
the size either
,
corresponding to the algorithms 1 and 2
respectively. It is assumed that these arrays are large enough to
accommodate the training pairs. They need not be initialized by the
caller. As in algorithm 7 it is possible to reduce
the size either ![]() or
or ![]() but not both. Doing so results
in a constant 2:1 space savings but for clarity we present the
algorithm using complete arrays.
but not both. Doing so results
in a constant 2:1 space savings but for clarity we present the
algorithm using complete arrays.
In algorithm 8 we remark that one should escape
after the ![]() computation in the event of a zero probability observation.
Also, the self-check of proposition 3 has a particularly simple
interpretation here: if one accumulates all contributions
to
computation in the event of a zero probability observation.
Also, the self-check of proposition 3 has a particularly simple
interpretation here: if one accumulates all contributions
to
![]() , doubling those corresponding to substitutions, the result is
exactly
, doubling those corresponding to substitutions, the result is
exactly ![]() .
.
We now illustrate by example that
one has no guarantee of convergence to a
global optimum. Let ![]() and
and ![]() provide the sole training
pair. If the probability of substitutions
provide the sole training
pair. If the probability of substitutions ![]() and
and ![]() are
are ![]() ,
and that of left-inserting
,
and that of left-inserting ![]() is also
is also ![]() , and left-inserting
, and left-inserting ![]() has probability
has probability ![]() , then learning converges to a local optimum in
which these operations have probability
, then learning converges to a local optimum in
which these operations have probability ![]() ,
, ![]() ,
, ![]() , and
, and ![]() respectively. The algorithm has in effect chosen to edit
respectively. The algorithm has in effect chosen to edit ![]() into
into ![]() by substituting
by substituting ![]() , then
, then ![]() and finally left-inserting
and finally left-inserting ![]() . At
convergence the pair's distance is
. At
convergence the pair's distance is ![]() bits. But it is clearly
better to left-insert
bits. But it is clearly
better to left-insert ![]() and perform two
and perform two ![]() substitutions.
Initializing the edit operations near to this objective leads learning
to the desired solution and the pair's distance is reduced to about
substitutions.
Initializing the edit operations near to this objective leads learning
to the desired solution and the pair's distance is reduced to about
![]() bits. Initializing the four parameters to
bits. Initializing the four parameters to ![]() yields a
third local maximum giving distance
yields a
third local maximum giving distance ![]() bits.
bits.
|
String edit distance is a very simple example of stochastic transduction. Using it to ground our discussion we now return to more general observations.
The costs employed in the edit distance computation depend only on the targets of the edit operations. They are independent of the context in which the edit operation occurs. Yet in most naturally occurring edit processes the likelihood of an edit operation depends strongly on the context in which the operation occurs. Within the FGM framework one may strengthen the model for edit distance so that the cost of an edit operation depends on the context in which that operation is performed. Insertion and deletion costs can depend on one or more positions of trailing context in a single string while substitution costs can depend on a joint context constructed from both strings. This modeling technique should lead to more powerful similarity functions and is applicable to transducers in general.
Context models may also be built by encoding context into the state
space. To do this one limits observation models to trivial
probability functions that assign probability ![]() to a single alphabet
member. After passing over an edge one then has certain knowledge of
the most recent symbol. Beyond this the graph can be designed so that
arrival in a state implies exact knowledge of a trailing finite
context of any desired length. In effect the modeling work is
moved entirely to the choice models. Having arrived at a vertex the
choice model predicts the next symbol conditioned on the past. Note
that this technique is an example of something that does not
generalize to continuous observations.
to a single alphabet
member. After passing over an edge one then has certain knowledge of
the most recent symbol. Beyond this the graph can be designed so that
arrival in a state implies exact knowledge of a trailing finite
context of any desired length. In effect the modeling work is
moved entirely to the choice models. Having arrived at a vertex the
choice model predicts the next symbol conditioned on the past. Note
that this technique is an example of something that does not
generalize to continuous observations.
To specify simple stochastic edit distance, we must learn only a
single ![]() table. With contexts, many more free parameters are
added to the model. In principle very large context models can be
built, but in practice their size is limited by the amount of training
data available increasing the need for MDL or MAP guided optimization.
table. With contexts, many more free parameters are
added to the model. In principle very large context models can be
built, but in practice their size is limited by the amount of training
data available increasing the need for MDL or MAP guided optimization.
The learning of a ![]() -way transducer's parameters represents one
formalization of what the authors have called the metric
learning paradigm. The training set may be regarded as positive
examples of the are similar concept and after learning, the
negated logarithm of the FGM's joint evaluation or conditional
evaluation is viewed as a measure of dissimilarity. The
mathematical metric axioms are not in general satisfied so by ``metric
learning'' we really mean any learned quantification of similarity or
dissimilarity.
-way transducer's parameters represents one
formalization of what the authors have called the metric
learning paradigm. The training set may be regarded as positive
examples of the are similar concept and after learning, the
negated logarithm of the FGM's joint evaluation or conditional
evaluation is viewed as a measure of dissimilarity. The
mathematical metric axioms are not in general satisfied so by ``metric
learning'' we really mean any learned quantification of similarity or
dissimilarity.
This idea applies beyond string settings and for processes more complex than
our definition of transduction which specifies that a tuple observation is
grown from left to right by concatenation.
The string edit distance DAG need not be viewed as arising from ![]() -way
transduction. The salient characteristic that implements metric learning
is that some edges observe both strings while others see only one.
It is not essential that as one moves from source to sink the string
positions considered within each tuple position also move from left to right.
-way
transduction. The salient characteristic that implements metric learning
is that some edges observe both strings while others see only one.
It is not essential that as one moves from source to sink the string
positions considered within each tuple position also move from left to right.
It is then clear that distances analogous to string edit distance may be defined for objects whose natural growth description is more complex than the linear DAG that corresponds to a string. We do not fully develop this direction but now make precise the corresponding DAG structure.
In the case of edit distance each FGM vertex faces three choices. Two
choices correspond to single symbol generation, and a third choice
selects joint generation. One may view the resulting graph as a
product of two linear FGMs, each of which grows a single string from
left to right. We now generalize this notion. Given two FGMs
![]() we define the generation DAG of the product FGM denoted
we define the generation DAG of the product FGM denoted
![]() as follows:
as follows:
It is readily verified that
![]() has a single source and
sink, and that each path corresponds to a permutation of the joint
observation tuple so that after specifying the necessary choice and
observation models, a well-formed SFGM results.
has a single source and
sink, and that each path corresponds to a permutation of the joint
observation tuple so that after specifying the necessary choice and
observation models, a well-formed SFGM results.
In this section we relate FGMs to three models in
widespread use: hidden Markov models, stochastic context free grammars,
and normal mixtures. The problem of optimizing the ![]() return of
a fixed portfolio is also shown to correspond to a trivial FGM.
We focus on reduction of these problems in standard form to FGMs but remark that
any of them may be improved by using MDL or MAP guided optimization
as described earlier.
return of
a fixed portfolio is also shown to correspond to a trivial FGM.
We focus on reduction of these problems in standard form to FGMs but remark that
any of them may be improved by using MDL or MAP guided optimization
as described earlier.
A hidden Markov model (HMM) is an automaton that changes state
stochastically after generating an observation. See [21,14]
for reviews. Its state transitions are given by a
stochastic ![]() matrix
matrix ![]() , a vector
, a vector ![]() gives the probability
of starting in each of its
gives the probability
of starting in each of its ![]() states, an output function
states, an output function ![]() is
associated with each state
is
associated with each state ![]() , and there are one or more designated
final states. As time passes the machine changes states and
generates observations which form an output time series.
, and there are one or more designated
final states. As time passes the machine changes states and
generates observations which form an output time series.
An HMM is essentially a ![]() -way stochastic transducer restricted so
that all transitions from a state specify the same observation
model and generate a single observation component (
-way stochastic transducer restricted so
that all transitions from a state specify the same observation
model and generate a single observation component (![]() ).
If there are more than one possible starting
states then the entire corresponding FGM is preceded by a choice that
plays the role of vector
).
If there are more than one possible starting
states then the entire corresponding FGM is preceded by a choice that
plays the role of vector ![]() . The edges leading to the sink are
weighted one or zero according to membership in the set of final
states.
. The edges leading to the sink are
weighted one or zero according to membership in the set of final
states.
Because output distributions are associated with states not edges in an HMM,
every FGM edge leaving a state is associated with the same distribution. For
this reason the transducer reduction can be simplified by eliminating
the ![]() states whose only purpose is to remember the previous state.
So if the HMM states are denoted
states whose only purpose is to remember the previous state.
So if the HMM states are denoted
![]() then the FGM states
are just
then the FGM states
are just ![]() where the superscript corresponds to time.
where the superscript corresponds to time.
This reduction of an HMM to an FGM amounts to the simple unfolding in time of the HMM's operation and is therefore done with no loss of efficiency. In some sense it is a simpler representation of the HMM because the temporal order of events has been made explicit.
Reduction in the other direction is problematic. Given a finite alphabet it is not hard to construct an equivalent HMM, i.e. one that imposes the same extrinsic probability distribution. But the canonical such machine may have exponentially more states because an FGM can generate observations in arbitrary order. Moreover, since an FGM can generate observations jointly, the standard HMM formulae for reestimation do not apply. Finally, an FGM that generates joint continuous observations will correspond to an HMM only if these joint densities are trivial, i.e. a product of independent terms. This suggests that FGMs may be more expressive than HMMs.
We now discuss an important variation: time duration HMMs
[17,25] and sketch their rederivation in FGM terms
illustrating the utility of parameterized choice models. See
[14] pages 218-221 for a brief review. If in a conventional HMM a
state transitions to itself with probability ![]() , then duration in that
state is geometrically distributed, i.e. as
, then duration in that
state is geometrically distributed, i.e. as ![]() . This
functional form restricts the model's ability to match the
characteristics of some applications such as phoneme recognition.
. This
functional form restricts the model's ability to match the
characteristics of some applications such as phoneme recognition.
In an ordinary HMM, diagonal transition matrix entries give the
self-transition probabilities. These will be modeled separately so
![]() is assumed to have a zero diagonal. The reduction of a time
duration HMM to an FGM starts with the same state set
is assumed to have a zero diagonal. The reduction of a time
duration HMM to an FGM starts with the same state set ![]() but
requires an additional set
but
requires an additional set ![]() . Associated with a
state
. Associated with a
state ![]() is a parameterized choice model that assigns a
probability to each possible state duration
is a parameterized choice model that assigns a
probability to each possible state duration ![]() from
from ![]() .
Edges exist from
.
Edges exist from ![]() to states
to states
![]() and along each,
and along each,
![]() observations are generated according to the same
distribution. To express this strictly within the FGM framework a
linear sequence of
observations are generated according to the same
distribution. To express this strictly within the FGM framework a
linear sequence of ![]() edges is necessary with a single
observation model attached to each. Associated with
edges is necessary with a single
observation model attached to each. Associated with
![]() is a simple discrete choice model induced by transition matrix
is a simple discrete choice model induced by transition matrix ![]() .
Edges are then directed to the corresponding
.
Edges are then directed to the corresponding
![]() state
with no attached observation model. Notice that since the diagonal of
state
with no attached observation model. Notice that since the diagonal of
![]() is zero there is no edge leading to
is zero there is no edge leading to
![]() . Even though
the choice model associated with each
. Even though
the choice model associated with each ![]() state has infinite domain,
the observation is finite so only a bounded number of edges are
included in the FGM.
state has infinite domain,
the observation is finite so only a bounded number of edges are
included in the FGM.
The simplest such infinite choice model has a parameter for every
duration value - a nonparametric approach. Since the training set
is finite this reduces to a standard discrete choice model which is
easily maximized. Because of limited training data one might prefer a
model with fewer parameters. A simple way to reduce parameters is to
group them into bins and assume that within a bin probability is
uniform. For example bin sizes might be
![]() . Here
duration
. Here
duration ![]() lies in the first bin, durations
lies in the first bin, durations ![]() in the second,
in the second,
![]() in the third, and so on. Parametric models may also be
used.
in the third, and so on. Parametric models may also be
used.
We close our discussion of HMMs with the topic of nonemitting
states, i.e. states that do not generate any output. These
complicate our reduction to FGMs and conventional processing as well
since cycles among them may have unbounded duration. Common practice
is to preprocess models with such states in order to eliminate
self-cycles. Denote by ![]() the set of nonemitting states and by
the set of nonemitting states and by ![]() the rest. Now suppose a transition occurs from an ordinary state to
a member of
the rest. Now suppose a transition occurs from an ordinary state to
a member of ![]() . The next transition may leave
. The next transition may leave ![]() immediately or cycle
through its states for some time before doing so. But since no
observations are generated we are merely interested in the ultimate
departure event. For each state in
immediately or cycle
through its states for some time before doing so. But since no
observations are generated we are merely interested in the ultimate
departure event. For each state in ![]() it is straightforward to
compute the probability of ultimately exiting to one of the states in
it is straightforward to
compute the probability of ultimately exiting to one of the states in
![]() . These values become entries in the transition matrix
associated with that state. All entries associated with
self-transitions among
. These values become entries in the transition matrix
associated with that state. All entries associated with
self-transitions among ![]() are set to zero. This modified
machine will impose the same extrinsic distribution as the original
but is free of nonemitting cycles and may be reduced to an FGM.
are set to zero. This modified
machine will impose the same extrinsic distribution as the original
but is free of nonemitting cycles and may be reduced to an FGM.
A stochastic context free grammar (SCFG) is a conventional
context free grammar [13] with a probability attached to each
production such that for every nonterminal ![]() the probabilities
attached to all productions ``
the probabilities
attached to all productions ``
![]() '' sum to unity.
Applied to a sentence of finite length these grammars have an
interesting recursive FGM structure. Baum-Welch/EM may then be used
to learn the attached probabilities from a corpus of training
sentences. The result is essentially the same as the inside-outside algorithm described in [21].
'' sum to unity.
Applied to a sentence of finite length these grammars have an
interesting recursive FGM structure. Baum-Welch/EM may then be used
to learn the attached probabilities from a corpus of training
sentences. The result is essentially the same as the inside-outside algorithm described in [21].
We assume the grammar ![]() is in Chomsky normal form and use
is in Chomsky normal form and use ![]() to
denote the input sentence. Viewing
to
denote the input sentence. Viewing ![]() as a stochastic
generator of strings each nonterminal
as a stochastic
generator of strings each nonterminal ![]() may expand into sentences of
many lengths. We write
may expand into sentences of
many lengths. We write
![]() to denote
the probability that
to denote
the probability that ![]() will generate the substring of
will generate the substring of ![]() consisting of its
consisting of its ![]() th through
th through ![]() th positions. In particular the
probability of
th positions. In particular the
probability of ![]() is
is
![]() where
where ![]() denotes the length of
denotes the length of ![]() and
and ![]() is the start symbol. For a
terminal
is the start symbol. For a
terminal ![]() ,
,
![]() if
if ![]() and
and
![]() , and zero otherwise. The SCFG is a probability function
over all sentences, so that it is a subprobability model for those of
any fixed length. For this reason null models (described earlier) are
employed in the construction to truncate the normally infinite
generation process.
, and zero otherwise. The SCFG is a probability function
over all sentences, so that it is a subprobability model for those of
any fixed length. For this reason null models (described earlier) are
employed in the construction to truncate the normally infinite
generation process.
The FGM corresponding to ![]() restricted to length
restricted to length ![]() is a recursive
construction starting with the start symbol. We name the top level
FGM
is a recursive
construction starting with the start symbol. We name the top level
FGM
![]() because it computes the probability of
because it computes the probability of ![]() applied to
applied to ![]() . The construction is the same for each
nonterminal
. The construction is the same for each
nonterminal ![]() with corresponding productions
with corresponding productions
![]() where
where ![]() denotes the number of productions of the form ``
denotes the number of productions of the form ``
![]() ''. The FGM
''. The FGM
![]() has
has ![]() edges from
source to sink and computes
edges from
source to sink and computes
![]() . Its
single choice model corresponds to the probabilities associated with
. Its
single choice model corresponds to the probabilities associated with
![]() in the grammar. Each edge generates observations
in the grammar. Each edge generates observations ![]() and the attached models are denoted
and the attached models are denoted
![]() where each
where each
![]() is
defined as follows:
is
defined as follows:
![\begin{displaymath}
P(BC \rightarrow t[i \ldots j]) =
\sum_{k=0}^{j-i-1} P(B ...
...rrow t[i \ldots i+k]) \cdot
P(C \rightarrow t[j-k \ldots j])
\end{displaymath}](img488.gif)
Each FGM's
![]() and
and
![]() generate
strictly shorter substrings of
generate
strictly shorter substrings of ![]() than does
than does
![]() whence the recursion is bounded and ultimately descends to
productions of the form
whence the recursion is bounded and ultimately descends to
productions of the form
![]() described above.
The choice models are tied across occurrences of each FGM
described above.
The choice models are tied across occurrences of each FGM
![]() in this recursive hierarchy.
in this recursive hierarchy.
The time and space complexity of the resulting model follows easily
from an analysis of its structure. There are ![]() FGMs of the
form
FGMs of the
form
![]() and
and ![]() of the form
of the form
![]() .
The first kind contains
.
The first kind contains ![]() edges while the second has
edges while the second has ![]() edges. The result is
edges. The result is ![]() time and space complexity. The same
counting of FGMs and edges demonstrates that complexity is linear in
the grammar's size.
time and space complexity. The same
counting of FGMs and edges demonstrates that complexity is linear in
the grammar's size.
Beyond emulating conventional SCFGs, our FGM construction suggests
more complex models. For example, it is possible to learn a
probability for each production conditioned on the length of the
sentence it generates. Here the single value associated with each
production is replaced with a vector of probabilities indexed by
sentence length. The vector's length may be set to the maximum length
of a sentence in the training corpus. The result is a model which
generates only sentences of finite length. More generally each vector
position may correspond to a range of lengths, e.g. less than 5,
between 6 and 20, 21 and over. If the final range is open-ended then the
model generates sentences of unbounded length, as does a SCFG. This
new model has more parameters, but given enough training data may
outperform an SCFG. To implement it one merely ties the choice
models associated with each instance of each FGM
![]() differently.
In the construction above they are all tied. Instead we
tie the choice model for
differently.
In the construction above they are all tied. Instead we
tie the choice model for
![]() to
to
![]() provided
provided ![]() , i.e. both instances generate output of the same length.
, i.e. both instances generate output of the same length.
A ![]() -component normal mixture is a probability density function of
the form:
-component normal mixture is a probability density function of
the form:
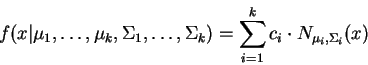
where
![]() ,
, ![]() for
for ![]() , and
, and
![]() denotes a multivariate normal density. Such a mixture
corresponds to a trivial FGM that contains exactly
denotes a multivariate normal density. Such a mixture
corresponds to a trivial FGM that contains exactly ![]() DAG edges, each
from source to sink, and a normal density along each. The FGM's
single choice model corresponds to the mixing parameters
DAG edges, each
from source to sink, and a normal density along each. The FGM's
single choice model corresponds to the mixing parameters
![]() . Unlike transduction, HMMs, and SCFGs, normal
mixtures are an example of an FGM which generates an observation
tuple of fixed finite dimension. They may be used as the observation
model along any edge in a parent FGM. Our earlier reduction of HMMs
to FGMs then results in the mixture-density HMMs widely used in speech
recognition. To illustrate the variations possible we observe that
tying every component with the same index to a single density yields
the semi-continuous variation [15].
. Unlike transduction, HMMs, and SCFGs, normal
mixtures are an example of an FGM which generates an observation
tuple of fixed finite dimension. They may be used as the observation
model along any edge in a parent FGM. Our earlier reduction of HMMs
to FGMs then results in the mixture-density HMMs widely used in speech
recognition. To illustrate the variations possible we observe that
tying every component with the same index to a single density yields
the semi-continuous variation [15].
Our final example consists of a problem that is not strictly speaking a
stochastic probability model but nevertheless fits easily into the FGM
formalism. Given stocks
![]() and observations of
their returns over many fixed time periods, the objective is to decide
how much of each should be held in an optimal investment portfolio. A
trivial reduction to FGMs results in a simple iterative algorithm.
This problem is considered in [9] where the same algorithm,
essentially a rediscovery of Baum-Welch/EM, is described.
The multiplicative update perspective of [9] is
essentially the growth transform of [3].
and observations of
their returns over many fixed time periods, the objective is to decide
how much of each should be held in an optimal investment portfolio. A
trivial reduction to FGMs results in a simple iterative algorithm.
This problem is considered in [9] where the same algorithm,
essentially a rediscovery of Baum-Welch/EM, is described.
The multiplicative update perspective of [9] is
essentially the growth transform of [3].
We describe this problem using the notation of [9] and
reduce it to an FGM. A stock which appreciates by ![]() in
say one month, is said to have a return of
in
say one month, is said to have a return of ![]() . The returns of
each stock over time period
. The returns of
each stock over time period ![]() forms a vector denoted
forms a vector denoted ![]() . We use
stochastic vector
. We use
stochastic vector ![]() to denote our portfolio allocation and the
portfolio's return over period
to denote our portfolio allocation and the
portfolio's return over period ![]() is then
is then ![]() . This is
captured by a simple FGM consisting of a
. This is
captured by a simple FGM consisting of a ![]() -way choice corresponding
to
-way choice corresponding
to ![]() with each edge leading directly to the sink. An unnormalized
observation model is attached to each edge and assumes the value of
the selected stock's return. Given
with each edge leading directly to the sink. An unnormalized
observation model is attached to each edge and assumes the value of
the selected stock's return. Given ![]() observations
observations
![]() ,
and letting
,
and letting
![]() denote the diagonal matrix formed from
denote the diagonal matrix formed from
![]() , one Baum-Welch/EM iteration is given by:
, one Baum-Welch/EM iteration is given by:
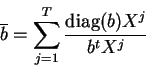
after ![]() is normalized to have unity sum. This
matches the equation given in [9]. Assuming the
is normalized to have unity sum. This
matches the equation given in [9]. Assuming the ![]() occur with equal probability then maximizing the training set's
likelihood also maximizes our expected log return from the portfolio.
occur with equal probability then maximizing the training set's
likelihood also maximizes our expected log return from the portfolio.
Pearl's Bayes nets [20], also known as graphical models [16], can
be represented in their simplest forms as FGMs in which vertices
correspond to variables, edge weights to conditional probabilities,
and vertex a posteriori probabilities (![]() ) to belief.
More complex networks can still be represented as FGMs although the
reduction is more involved. The relationship between these
networks and hidden Markov models is elucidated in [27].
) to belief.
More complex networks can still be represented as FGMs although the
reduction is more involved. The relationship between these
networks and hidden Markov models is elucidated in [27].
Exploring the relationship of FGMs to error correcting codes such as those based on trellises, and the recently developed class of turbo codes [5], is a subject for future work. We wonder broadly whether our framework's generality might lead to better codes, and in particular whether DAGs that encode nonlinear time orderings might have value. Such a possibility is suggested by [29,28]. The relationship between Turbo codes and Bayes nets is examined in [18] and understanding the relationship of FGMs to this specific outlook is another interesting area for future work.
This document was generated using the LaTeX2HTML translator Version 2K.1beta (1.47)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -image_type gif -nonext_page_in_navigation -noprevious_page_in_navigation -up_url ../main.html -up_title 'Publication homepage' -numbered_footnotes fgm.tex
The translation was initiated by Peter N. Yianilos on 2002-06-30