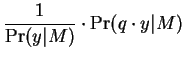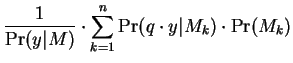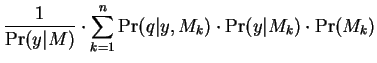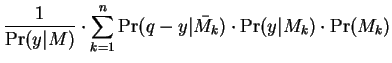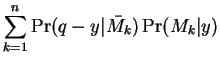Up: Publication homepage
Feature-Based Face Recognition Using Mixture-Distance
Ingemar J. Cox - Joumana Ghosn - Peter
N. Yianilos1
Abstract:
We consider the problem of feature-based face recognition in the
setting where only a single example of each face is available for
training. The
mixture-distance technique we introduce achieves
a recognition rate of
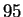
% on a database of 685 people in which each
face is represented by
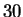
measured distances. This is currently the
best recorded recognition rate for a feature-based system applied to a
database of this size. By comparison, nearest neighbor search using
Euclidean distance yields
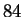
%.
In our work a novel distance function is constructed based on
local second order statistics as estimated by modeling the
training data as a mixture of normal densities. We report on
the results from mixtures of several sizes.
We demonstrate that a flat mixture of mixtures performs
as well as the best model and therefore represents an
effective solution to the model selection problem. A mixture
perspective is also taken for individual Gaussians to choose
between first order (variance) and second order (covariance)
models. Here an approximation to flat combination is
proposed and seen to perform well in practice.
Our results demonstrate that even in the absence of multiple training
examples for each class, it is sometimes possible to infer from a
statistical model of training data, a significantly improved distance
function for use in pattern recognition.
Keywords -- Face Recognition, Mixture Models, Statistical Pattern Recognition,
Improved Distance Metrics.
Introduction
Research towards automatic face recognition began in the late
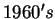 and divides roughly into two lines of inquiry: feature based
approaches which rely on a feature set small in comparison to the
number of image pixels, and direct image methods which involve no
intermediate feature extraction stage. There are distinct advantages
to both approaches and this is discussed further in Section 2
where previous work is summarized.
and divides roughly into two lines of inquiry: feature based
approaches which rely on a feature set small in comparison to the
number of image pixels, and direct image methods which involve no
intermediate feature extraction stage. There are distinct advantages
to both approaches and this is discussed further in Section 2
where previous work is summarized.
This paper's general motivation is to better understand what is
limiting the performance of feature based systems. The structure of
such systems varies widely but three major components may be
identified: the definition of a feature set, the extraction of these
features from an image, and the recognition algorithm.
We focus on feature sets derived from the location of anatomical features
in frontal or nearly frontal views. Our particular feature set definition
involves 30 distances derived from 35 measured locations.
Our main interest is in the recognition algorithm's effect on
performance, so these 35 locations were determined by human
operators and recorded in the database. That is, errors associated
with feature extraction were kept to a minimum to highlight the errors
due to the recognition algorithm, although, in principle, automated
feature extraction is possible.
This is discussed
in greater detail in Section 3 where our experimental
database and framework is described.
If many images of each person are available, then each
individual may be considered a pattern class, and one can directly apply the methods of
statistical pattern recognition to build a model per person. A common
approach models each class as a normal density, so for each person
there is a corresponding mean feature vector and covariance matrix.
The probability of an unknown pattern conditioned on each model is
then easily computed. Using a prior distribution on the individuals
in the database (flat for example) the classification task is
completed in the standard Bayesian fashion by computing the a
posteriori probability of each person, conditioned on observation of
the query. If the computation is performed using  probabilities, it is slightly less expensive computationally and
the distance metric is the well known Mahalanobis distance.
probabilities, it is slightly less expensive computationally and
the distance metric is the well known Mahalanobis distance.
Given a large number of images for each person this approach would
further illuminate the recognition capacity of a given feature set.
However in practice we do not always have a large number of images of
each individual. In fact, it is not uncommon to have only a single
training example for each person, and it is this data sparsity that
distinguishes the current work from the traditional class modeling framework.
In this setting we assume that the
recognition algorithm consists of nearest neighbor search using some
distance function between feature vectors. The key questions are then
how does the distance function affect recognition rate, and what
can be done to find an effective metric?
Our experimental study uses a database of 685 individuals described
further in Section 3. Duplicate images are available
for 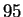 of these and form the queries we use to measure performance.
If standard Euclidean distance is used,
of these and form the queries we use to measure performance.
If standard Euclidean distance is used, 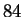 % of queries are
correctly classified. In statistical terms, Euclidean distance may be
viewed as corresponding to the assumption that each pattern vector is
a class generator with unit covariance and mean coinciding with the
pattern. Despite the sparsity of data, it would be surprising indeed
if there is nothing one can learn from the training data to improve
upon this assumption. To this end, we introduce the use of mixture-distance functions which are obtained by first modeling the
training data as a mixture of normal densities, and then using this
model in a particular way to measure distance. Our method increases
recognition performance to
% of queries are
correctly classified. In statistical terms, Euclidean distance may be
viewed as corresponding to the assumption that each pattern vector is
a class generator with unit covariance and mean coinciding with the
pattern. Despite the sparsity of data, it would be surprising indeed
if there is nothing one can learn from the training data to improve
upon this assumption. To this end, we introduce the use of mixture-distance functions which are obtained by first modeling the
training data as a mixture of normal densities, and then using this
model in a particular way to measure distance. Our method increases
recognition performance to 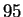 %, the highest recognition rate for a
feature-based system applied to a database of this size. These
functions are discussed later in Section
4 and explored in greater detail in [21].
%, the highest recognition rate for a
feature-based system applied to a database of this size. These
functions are discussed later in Section
4 and explored in greater detail in [21].
The use of mixture-distances immediately presents two model selection
problems: selection of the number of elements in the mixture, and the
more basic but sometimes ignored problem of choosing between first and
second order statistics for each component Gaussian. In both cases, we
implemented a very simple flat prior approach which our
experiments showed performs as well as the best individual model, as
described in Section 5.
The results of our experiments are
covered in Section 6. Finally,
Section 7 consists of concluding remarks and
suggested areas for further study.
Previous work
While research in automatic face recognition began in the late
 , progress has been slow. Recently there has been renewed
interest in the problem due in part to its numerous security
applications ranging from identification of suspects in police
databases to identity verification at automatic teller machines.
In this section, we briefly describe related work. We coarsely
categorize approaches as either feature based,
relying on a feature set small in comparison to the
number of image pixels, or direct image methods which involve no
intermediate feature extraction stage. Of course, direct image
methods may also extract features but the distinction is that such
features change significantly with variations in illumination. By
contrast, the feature based classification is intended to categorize
techniques that are robust to illumination conditions.
, progress has been slow. Recently there has been renewed
interest in the problem due in part to its numerous security
applications ranging from identification of suspects in police
databases to identity verification at automatic teller machines.
In this section, we briefly describe related work. We coarsely
categorize approaches as either feature based,
relying on a feature set small in comparison to the
number of image pixels, or direct image methods which involve no
intermediate feature extraction stage. Of course, direct image
methods may also extract features but the distinction is that such
features change significantly with variations in illumination. By
contrast, the feature based classification is intended to categorize
techniques that are robust to illumination conditions.
Direct methods included template
matching [1] and the more recent work of Turk and Pentland
[17] on ``eigenfaces''. Template matching is only effective when
the query and model images have the same scale, orientation and
illumination properties. This is a very restricted regime that is
unlikely to be found in many operating environments. Although recently
Brunelli and Poggio [2] compared a template matching
scheme similar to Baron's [1]with a feature-based method on
a database of  individuals and found their template matching
method to be superior, no generalization can be drawn from
these results which are ``clearly specific to our task and to our
implementation''.
individuals and found their template matching
method to be superior, no generalization can be drawn from
these results which are ``clearly specific to our task and to our
implementation''.
Turk and Pentland [17] have proposed a method of face
recognition based on principal component analysis. Each image of a
face maps to a single point in a very high-dimensional space in which
each dimension represents the intensity of an image pixel. They then
use principal component analysis to find the low-dimensional
projection of this space that best represents the data. Using simple
nearest neighbor classification in this space Pentland, Moghaddam and
Starner [12] report accuracy of 95% on a data base
containing about 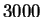 different faces. However, all images in this
test seem to be taken with little variation in viewpoint and lighting,
although with significant variation in facial expression. Since the
method is similar to, although more computationally efficient than
correlation based on pixel intensities, these results are consistent
with Moses et al's [10] conclusions that correlation
methods are relatively insensitive to variations in facial expression.
Moses has found that correlation methods are much more sensitive to
lighting and viewpoint variations, which raises questions about the
potential of the eigenfaces approach to extend to these viewing
conditions. However, see Pentland, Moghaddam and Starner for one
approach to handling view variation.
different faces. However, all images in this
test seem to be taken with little variation in viewpoint and lighting,
although with significant variation in facial expression. Since the
method is similar to, although more computationally efficient than
correlation based on pixel intensities, these results are consistent
with Moses et al's [10] conclusions that correlation
methods are relatively insensitive to variations in facial expression.
Moses has found that correlation methods are much more sensitive to
lighting and viewpoint variations, which raises questions about the
potential of the eigenfaces approach to extend to these viewing
conditions. However, see Pentland, Moghaddam and Starner for one
approach to handling view variation.
In principle, feature-based schemes can be made invariant to scale,
rotation and/or illumination variations and it is for this reason
that we are interested in them. Early work in this area
was first reported by Goldstein et al [4] in
which a ``face-feature questionnaire'' was manually completed for each
face in the database. Human subjects were then asked to identify
faces in databases ranging in size from 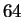 to
to 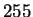 using
using 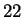 features. Interestingly, only
features. Interestingly, only 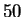 % accuracy was obtained.
% accuracy was obtained.
Subsequent work addressed the problem of automatically extracting
facial features. Kanade [7,9] described a system which
automatically extracted a set of facial features, computed a
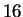 -dimensional feature vector based on ratios of distances (and
areas) between facial features, and compared two faces based on a sum
of distances. On a database of
-dimensional feature vector based on ratios of distances (and
areas) between facial features, and compared two faces based on a sum
of distances. On a database of 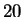 faces, Kanade achieved a
recognition rate of between
faces, Kanade achieved a
recognition rate of between 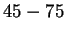 % using automatically extracted
facial features. It is interesting to note that
when our mixture contains just a single Gaussian, and only first order
statistics are employed (the off-diagonal covariance entries are
ignored), our approach reduces to Kanade's early work using
Euclidean distance weighted inversely by the variance of each feature.
% using automatically extracted
facial features. It is interesting to note that
when our mixture contains just a single Gaussian, and only first order
statistics are employed (the off-diagonal covariance entries are
ignored), our approach reduces to Kanade's early work using
Euclidean distance weighted inversely by the variance of each feature.
Perhaps because it was perceived as difficult to
automatically extract 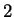 -dimensional facial features, significant
effort has been directed towards using face profiles
[5,6,8]. In this case, the automatic
extraction of features is a somewhat simpler one-dimensional problem.
Kaufman and Breeding reported a recognition rate of
-dimensional facial features, significant
effort has been directed towards using face profiles
[5,6,8]. In this case, the automatic
extraction of features is a somewhat simpler one-dimensional problem.
Kaufman and Breeding reported a recognition rate of 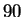 % using
facial profiles, but this was on a database of only
% using
facial profiles, but this was on a database of only 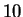 individuals.
Harmon et al reported a recognition rate of
individuals.
Harmon et al reported a recognition rate of 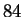 % on a
% on a 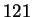 individual database using a Euclidean distance metric. Recognition
rates of almost
individual database using a Euclidean distance metric. Recognition
rates of almost 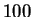 % are claimed using a classification scheme
based on set partitioning and Euclidean distance. However, these
experiments did not maintain disjoint training and test sets.
Subsequent work by Harmon et al
[5] did maintain a separate test set and reported
recognition accuracies of
% are claimed using a classification scheme
based on set partitioning and Euclidean distance. However, these
experiments did not maintain disjoint training and test sets.
Subsequent work by Harmon et al
[5] did maintain a separate test set and reported
recognition accuracies of 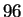 % on a database of
% on a database of 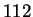 individuals.
individuals.
Kaufman and Breeding [8] compared their results with
human recognition of facial profiles and found that human performance
was not significantly better. This comparison highlights an obvious
problem: what is the classification capability of a set of features?
This is clearly a fundamental question, especially since it is unclear
what features the human visual system uses. After all, no amount of
subsequent processing can compensate for a feature set that lacks
discrimination ability. Perhaps because of this, most previous work has
concentrated on investigating alternative face representations while
paying little attention to the subsequent recognition algorithm. In
fact, the role of the recognition algorithm has
not been adequately addressed in the face
recognition literature, especially for moderately large databases
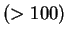 . In this paper we begin to do so by examining the
recognition rate of a
. In this paper we begin to do so by examining the
recognition rate of a 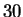 -dimensional feature vector on a
database of
-dimensional feature vector on a
database of 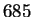 faces.
faces.
Experimental Database
Figure 1:
Manually identified facial features.
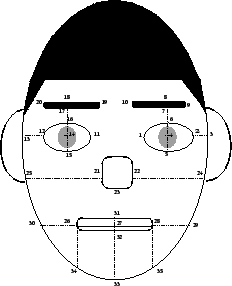 |
Figure (1) shows the 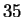 points that were manually
extracted from each face and Table (1) lists the
30-dimensional feature vector computed from these facial features. We
followed the point measurement system of [19] since the
Japanese portion of our database consisted of measured feature values
only, i.e. the original intensity images were unavailable. All distances are
normalized by the inter-iris distance to provide similarity
invariance.
points that were manually
extracted from each face and Table (1) lists the
30-dimensional feature vector computed from these facial features. We
followed the point measurement system of [19] since the
Japanese portion of our database consisted of measured feature values
only, i.e. the original intensity images were unavailable. All distances are
normalized by the inter-iris distance to provide similarity
invariance.
Our model database of 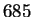 images is an amalgam of images selected
from several different sources as described below2:
1)
images is an amalgam of images selected
from several different sources as described below2:
1)
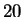 images from the UCSB database created by B.S. Manjunath
of UCSB,
2)
images from the UCSB database created by B.S. Manjunath
of UCSB,
2)
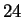 images from Weizmann Institute database which was obtained from
public domain ftp site from Weizmann Institute, courtesy of Yael Moses,
3)
images from Weizmann Institute database which was obtained from
public domain ftp site from Weizmann Institute, courtesy of Yael Moses,
3)
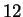 images from the MIT database which was down-loaded from the public
ftp site at MIT,
4)
images from the MIT database which was down-loaded from the public
ftp site at MIT,
4)
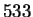 images from the NEC database obtained from NEC, Japan,
5)
images from the NEC database obtained from NEC, Japan,
5)
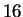 images from the database provided by Sandy Pentland of MIT
Media Lab,
6)
images from the database provided by Sandy Pentland of MIT
Media Lab,
6)
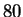 images from the Feret Database, courtesy of the Army Research
Laboratory.
The query database consists of
images from the Feret Database, courtesy of the Army Research
Laboratory.
The query database consists of 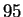 images from the following sources:
1)
images from the following sources:
1)
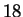 images from UCSB database,
2)
images from UCSB database,
2)
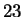 images from the Weizmann Institute database,
3)
images from the Weizmann Institute database,
3)
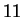 images from the MIT database,
4)
images from the MIT database,
4)
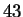 images from the NEC, Japan database.
Each element of the query database represents a second frontal view of
someone in the model database. Its size was severely limited by the
availability of such images.
images from the NEC, Japan database.
Each element of the query database represents a second frontal view of
someone in the model database. Its size was severely limited by the
availability of such images.
Table 1:
The 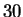 -dimensional feature vector.
-dimensional feature vector.
|
Feature |
Distance |
|
1 |
0.5 * ( (1,2) + (11,12) ) |
|
2 |
0.5 * ( (5,6) + (15,16) ) |
|
3 |
(3,13) |
|
4 |
(24,25) |
|
5 |
(29,30) |
|
6 |
(34,35) |
|
7 |
(26,34) |
|
8 |
(28,35) |
|
9 |
(26,28) |
|
10 |
(27,31) |
|
11 |
(27,32) |
|
12 |
(32,33) |
|
13 |
(23,31) |
|
14 |
(21,22) |
|
15 |
0.5 * ( (13,25) + (3,24) ) |
|
16 |
0.5 * ( (25,30) + (24,29) ) |
|
17 |
0.5 * ( (30,34) + (29,35) ) |
|
18 |
0.5 * ( (1,22) + (11,21) ) |
|
19 |
(10,19) |
|
20 |
0.5 * ( (2,9) + (12,20) ) |
|
21 |
0.5 * ( (9,10) + (19,20) ) |
|
22 |
0.5 * ( (11,19) + (1,10) ) |
|
23 |
0.5 * ( (6,7) + (16,17) ) |
|
24 |
0.5 * ( (7,8) + (17,18) ) |
|
25 |
0.5 * ( (18,19) + (8,10) ) |
|
26 |
0.5 * ( (18,20) + (8,9) ) |
|
27 |
(11,23) |
|
28 |
(1,23) |
|
29 |
0.5 * ( (1,28) + (11,26) ) |
|
30 |
0.5 * ( (12,13)+(2,3) ) |
|
Mixture Distance Functions
Given a database of facial feature vectors 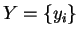 , each
corresponding to a different person, and a query
, each
corresponding to a different person, and a query 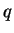 consisting of a facial feature vector for some unidentified
person assumed to be represented in
consisting of a facial feature vector for some unidentified
person assumed to be represented in 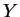 , our objective is to
locate the
, our objective is to
locate the  corresponding to
corresponding to 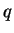 . In the absence of
error, and assuming no two people are exactly alike, we
would have only to search
. In the absence of
error, and assuming no two people are exactly alike, we
would have only to search 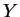 for an exact match to
for an exact match to 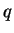 . But
in practice
. But
in practice 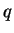 will not match anything in
will not match anything in 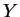 perfectly
because of many sources of error. These include feature
extraction errors associated with the human or algorithm which
constructed the feature vector from a photograph, variation in
the subject's pose, unknown camera optical characteristics,
and physical variation in the subject itself (e.g. expression,
aging, sickness, grooming, etc.) Clearly the nature of these
error processes should influence the way in which we compare
queries and database elements. The difficulty lies in the
fact that we can't directly observe them given that only a
single example of each person exists in
perfectly
because of many sources of error. These include feature
extraction errors associated with the human or algorithm which
constructed the feature vector from a photograph, variation in
the subject's pose, unknown camera optical characteristics,
and physical variation in the subject itself (e.g. expression,
aging, sickness, grooming, etc.) Clearly the nature of these
error processes should influence the way in which we compare
queries and database elements. The difficulty lies in the
fact that we can't directly observe them given that only a
single example of each person exists in 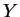 .
.
In this section we begin with a formal discussion but at a general
level in order to establish a clear conceptual framework.
Certain simplifying assumptions are then made which lead to a
practical approach to the problem of inferring something about
the error processes at work in our data. The final result is then a
simple formula for comparing queries with database elements in
the presence of error.
We imagine the observed feature vectors, whether database
elements or queries, to be the result of a two-stage
generative process. The first stage 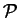 generates platonic
vectors
generates platonic
vectors 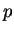 which are thought of as idealized representations
of each pattern class - in our case the facial features of
distinct humans. The second stage is the observation
process which generates the vectors we ultimately observe.
The first stage corresponds to inter-class variation,
i.e. between people, while the second stage captures
intra-class variation. The nature of the second process
depends on
which are thought of as idealized representations
of each pattern class - in our case the facial features of
distinct humans. The second stage is the observation
process which generates the vectors we ultimately observe.
The first stage corresponds to inter-class variation,
i.e. between people, while the second stage captures
intra-class variation. The nature of the second process
depends on 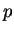 and we therefore denote it as
and we therefore denote it as 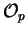 . We will
further assume that each
. We will
further assume that each 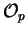 is a zero mean process, which
conceptually, adds observation noise to the platonic vector at
its center.
is a zero mean process, which
conceptually, adds observation noise to the platonic vector at
its center.
The probability 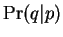 that a query
that a query 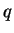 was generated by a
particular platonic
was generated by a
particular platonic 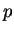 , is then computed by forming the
vector difference
, is then computed by forming the
vector difference 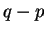 and evaluating
and evaluating 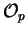 . This suggests
the notation:
. This suggests
the notation:
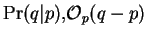 . Similarly the
probability
. Similarly the
probability 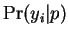 that a particular database element
that a particular database element
 was generated by
was generated by  is
is
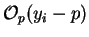 . Finally the
probability
. Finally the
probability 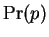 of
of 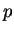 itself is just
itself is just 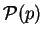 . To
judge how similar
. To
judge how similar 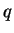 and
and  , the approach taken in
[21] is to focus on the probability of the 3-way
joint event consisting of the generation of
, the approach taken in
[21] is to focus on the probability of the 3-way
joint event consisting of the generation of 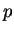 , followed by
its observation as
, followed by
its observation as 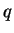 , followed by a second independent
observation as
, followed by a second independent
observation as  . Integrating over
. Integrating over 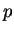 then gives
the probability that
then gives
the probability that 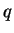 and
and  are independent observations
of a single platonic form.
are independent observations
of a single platonic form.
Our first simplifying assumption is that the  are
considered to be platonic. This eliminates the integral above
and is actually the assumption implicit in most nearest
neighbor pattern recognition methods. It amounts to imagining
that the query is a an observation of the database element -
not of some third (mutual) platonic element. One hopes that
are
considered to be platonic. This eliminates the integral above
and is actually the assumption implicit in most nearest
neighbor pattern recognition methods. It amounts to imagining
that the query is a an observation of the database element -
not of some third (mutual) platonic element. One hopes that  is
not too far from its
is
not too far from its 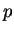 , and that the distribution of
observations about
, and that the distribution of
observations about  therefore approximates the
distribution about
therefore approximates the
distribution about 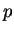 . So now we focus on the matter of
attributing to
. So now we focus on the matter of
attributing to  , an observation process
, an observation process 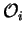 . Having
done this we can then compute
. Having
done this we can then compute 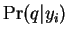 for each
for each  . We
will classify
. We
will classify 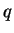 by choosing the largest such probability.
This is easily seen to be the same as maximizing
by choosing the largest such probability.
This is easily seen to be the same as maximizing 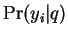 with a flat prior on
with a flat prior on 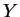 .
.
The mixture-distance method we introduce may be viewed
as a particular way, but by no means the only way to arrive at
an 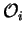 for each
for each  . Perhaps the simplest such
assignment gives each
. Perhaps the simplest such
assignment gives each  an identical
an identical 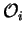 consisting of
a zero mean Gaussian process with unit covariance. Computing
probabilities as logarithms reveals that this is exactly the
same as the use of ordinary Euclidean distance and performing
a nearest neighbor search. It is helpful to visualize these
consisting of
a zero mean Gaussian process with unit covariance. Computing
probabilities as logarithms reveals that this is exactly the
same as the use of ordinary Euclidean distance and performing
a nearest neighbor search. It is helpful to visualize these
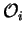 as hyper-spheres of identical dimension corresponding
to the unit distance (or equi-probability) surface arising
from the process. In this simple case such a sphere is located
about every database element so that the nature of the distance
function employed is the same everywhere in space - and in
every dimension.
as hyper-spheres of identical dimension corresponding
to the unit distance (or equi-probability) surface arising
from the process. In this simple case such a sphere is located
about every database element so that the nature of the distance
function employed is the same everywhere in space - and in
every dimension.
In contrast to this simple assignment, we may also consider
the ideal case in which each  is associated with its true
error process. Assuming these processes are zero mean
Gaussian, then the
is associated with its true
error process. Assuming these processes are zero mean
Gaussian, then the 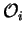 may now be visualized as a
hyper-ellipsoids of various sizes and shapes surrounding the
may now be visualized as a
hyper-ellipsoids of various sizes and shapes surrounding the
 . Unfortunately, as observed earlier, we don't have
enough data to reconstruct this picture and must therefore
turn to techniques which infer something about it from the few
data points available. The mixture-distance technique
is such a method which makes its inference based only on the
distribution of
. Unfortunately, as observed earlier, we don't have
enough data to reconstruct this picture and must therefore
turn to techniques which infer something about it from the few
data points available. The mixture-distance technique
is such a method which makes its inference based only on the
distribution of 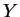 .
.
Suppose the observation process is extremely noisy - so much
so that most of the variation seen in 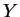 is due to noise not
to actual differences in facial characteristics. In this
extreme case, assuming for simplicity that the noise process
is Gaussian, the sample covariance matrix of
is due to noise not
to actual differences in facial characteristics. In this
extreme case, assuming for simplicity that the noise process
is Gaussian, the sample covariance matrix of 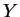 captures
mainly the characteristics of the observation process.
At the other extreme, if little noise is present, then most of
the variation in
captures
mainly the characteristics of the observation process.
At the other extreme, if little noise is present, then most of
the variation in 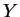 is due to actual differences between
individuals. Here there is no reason to expect the sample
covariance of
is due to actual differences between
individuals. Here there is no reason to expect the sample
covariance of 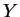 to tell us anything about the observation process.
to tell us anything about the observation process.
The main conceptual argument behind mixture-distance is that if 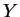 is
decomposed into a mixture, where each component is thought of as
covering some region of space, then within each region, observation
noise becomes the dominant component of the empirical distribution.
So as the number of mixture components increases, one hopes that
that the statistics of each region capture an increasingly accurate
estimate of the observation process. The
is
decomposed into a mixture, where each component is thought of as
covering some region of space, then within each region, observation
noise becomes the dominant component of the empirical distribution.
So as the number of mixture components increases, one hopes that
that the statistics of each region capture an increasingly accurate
estimate of the observation process. The 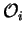 assigned to
each
assigned to
each  is then determined by the region into which
is then determined by the region into which  falls.
falls.
Consider the data-rich limit in which 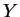 contains many
observations of each person, and the mixture contains as many
components as there are distinct individual's. Here, given a
perfect unsupervised mixture density estimation procedure,
one would express
contains many
observations of each person, and the mixture contains as many
components as there are distinct individual's. Here, given a
perfect unsupervised mixture density estimation procedure,
one would express 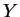 as a mixture of densities where each
component corresponds exactly to the error process for a
particular individual, and is centered at the mean feature
value for that individual. In this extreme case, attributing
to
as a mixture of densities where each
component corresponds exactly to the error process for a
particular individual, and is centered at the mean feature
value for that individual. In this extreme case, attributing
to  the error process from its region of space, is
exactly the right thing to do. In practice one employs
mixtures with far fewer components and hopes that the
resulting decomposition of space makes the observation process
dominant or at least significant. Said another way, one hopes
that before reaching the data-rich case above, the decompositions
arrived at by unsupervised mixture density estimation, begin
to reveal useful information about the observation processes
at work in each region of space.
the error process from its region of space, is
exactly the right thing to do. In practice one employs
mixtures with far fewer components and hopes that the
resulting decomposition of space makes the observation process
dominant or at least significant. Said another way, one hopes
that before reaching the data-rich case above, the decompositions
arrived at by unsupervised mixture density estimation, begin
to reveal useful information about the observation processes
at work in each region of space.
So returning to our imagined hyper-ellipsoids surrounding each
 , mixture-distance may be thought of as assigning
, mixture-distance may be thought of as assigning 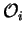 based on the mixture component which contains
based on the mixture component which contains  . A
simplified picture would show the
. A
simplified picture would show the  in particular region
space surrounded by hyper-ellipsoids selected for that region.
The imagery above is a simplification of the true situation
because each
in particular region
space surrounded by hyper-ellipsoids selected for that region.
The imagery above is a simplification of the true situation
because each  belongs stochastically, not deterministically,
to a given region. The
belongs stochastically, not deterministically,
to a given region. The 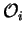 assigned to it is then a
mixture not a single Gaussian.
assigned to it is then a
mixture not a single Gaussian.
Also, in the examples above, we assumed that the actual
observation processes were zero mean Gaussian. We remark that
given even a single face and multiple observations arising
from different feature extraction agents (whether human
operators or algorithms), a less restrictive assumption is
that the error process is itself a mixture of zero mean
Gaussians - one for each agent. We make this remark because
it is entirely possible that some of the components identified
by unsupervised mixture density estimation, may correspond to
different feature extractors not to different kinds of faces.
In general the structure discovered might sometimes correspond
to semantic labels such as as gender, age, racial identity -
but there is no reason to believe that such a correspondence
is necessary in order for the hidden structure to lead to an
improved distance function.
We now proceed to more formally derive our formula for
mixture-distance. A finite mixture model 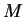 is a collection
of probability models
is a collection
of probability models
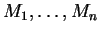 and non-negative mixing
parameters
and non-negative mixing
parameters
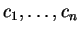 summing to unity, such that:
summing to unity, such that:
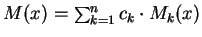 .
.
Let
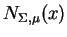 denote the multi-variate normal
density (Gaussian) having covariance
denote the multi-variate normal
density (Gaussian) having covariance 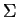 and expectation
and expectation
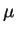 . When the elements
. When the elements 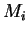 of
of 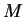 are Gaussian,
are Gaussian, 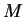 is
said to be a Gaussian or Normal mixture. Given a finite set
of vectors
is
said to be a Gaussian or Normal mixture. Given a finite set
of vectors
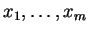 , the task of estimating the
parameters of a normal mixture model which explains the data
well, has been heavily studied. The well known expectation
maximization method (EM) [13] is perhaps that best
known approach and we adopt it for our experiments using
k-means clustering to provide a starting point.
, the task of estimating the
parameters of a normal mixture model which explains the data
well, has been heavily studied. The well known expectation
maximization method (EM) [13] is perhaps that best
known approach and we adopt it for our experiments using
k-means clustering to provide a starting point.
We now assume that an 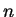 -element normal mixture model
-element normal mixture model 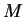 has been built to model the database elements
has been built to model the database elements 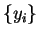 and we refer to
this as the empirical distribution. Each mixture element
and we refer to
this as the empirical distribution. Each mixture element
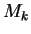 is a normal density
is a normal density
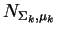 and we note by
and we note by
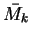 the zero mean density
the zero mean density
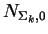 . So
. So
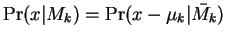 . The system's query to
be classified is denoted
. The system's query to
be classified is denoted 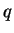 . Using the mixing probabilities
. Using the mixing probabilities
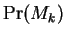 obtained from EM, we may then compute the a
posteriori component probabilities
obtained from EM, we may then compute the a
posteriori component probabilities 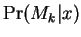 . These may
be thought of as a stochastic indication of
. These may
be thought of as a stochastic indication of 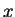 's membership
in each of the mixture's components. We will attribute
to each
's membership
in each of the mixture's components. We will attribute
to each  an
an 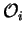 which is a mixture of the
which is a mixture of the 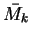 determined by these stochastic membership values. This
is explained best by the derivation which follows:
determined by these stochastic membership values. This
is explained best by the derivation which follows:
where
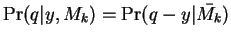 and
and
It is this formulation we use for all of our experiments.
In [21] various more complicated expressions are given
corresponding to weaker or different assumptions.
Finally we observe that in the case of one mixture element 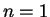 ,
mixture-distance reduces to the Mahalanobis distance from the
query
,
mixture-distance reduces to the Mahalanobis distance from the
query 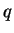 to average face
to average face 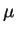 .
.
Observe first that the term 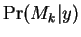 does not depend on
the query and may therefore be pre-computed and recorded as
part of the database. Next recall from the basic theory of
multi-variate normal densities and quadratic forms, that for
each mixture element
does not depend on
the query and may therefore be pre-computed and recorded as
part of the database. Next recall from the basic theory of
multi-variate normal densities and quadratic forms, that for
each mixture element 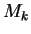 we may find a basis in which the
density's covariance matrix is diagonal. This is of course
accomplished via unitary matrix
we may find a basis in which the
density's covariance matrix is diagonal. This is of course
accomplished via unitary matrix 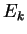 whose rows consists of
the eigenvectors of
whose rows consists of
the eigenvectors of 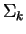 . If the vectors
. If the vectors 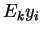 are
all recorded in the database as well, and
are
all recorded in the database as well, and 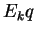 is computed
before the database search begins, then the computation time
for mixture distance becomes linear, not quadratic in the
dimension of feature space. Note, however, that
is computed
before the database search begins, then the computation time
for mixture distance becomes linear, not quadratic in the
dimension of feature space. Note, however, that 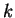 vectors
must be stored for each database element
vectors
must be stored for each database element  . This storage
requirement can be reduced by the ``hard VQ'' approximation.
. This storage
requirement can be reduced by the ``hard VQ'' approximation.
Focusing again on 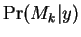 we may make another simplifying
assumption in order to further reduce computation and storage space.
Note that
we may make another simplifying
assumption in order to further reduce computation and storage space.
Note that
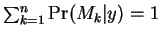 .
The assumption which is typically referred to as Hard VQ (where
VQ stands for ``vector quantization''), consists of replacing
this discrete probability function on
.
The assumption which is typically referred to as Hard VQ (where
VQ stands for ``vector quantization''), consists of replacing
this discrete probability function on 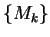 by a simpler
function which assumes value
by a simpler
function which assumes value 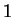 at a single point where the
original function is maximized, and zero elsewhere.
Conceptually this corresponds to hard decision
boundaries and we would expect it to affect the resulting
computation significantly only when a point
at a single point where the
original function is maximized, and zero elsewhere.
Conceptually this corresponds to hard decision
boundaries and we would expect it to affect the resulting
computation significantly only when a point  is near to a
decision boundary. We will then refer to the original
formulation as Soft VQ.
is near to a
decision boundary. We will then refer to the original
formulation as Soft VQ.
Space savings result from the hard VQ assumption since we must
now record in the database, each  expressed in only a
single Eigenbasis corresponding to the distinguished
expressed in only a
single Eigenbasis corresponding to the distinguished 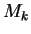 (which must also be identified). This scheme is then a linear
time and space prescription for mixture-distance computation.
(which must also be identified). This scheme is then a linear
time and space prescription for mixture-distance computation.
Model Selection Techniques
In any statistical modeling approach in which the size and
nature of the models (their configuration) used may vary, one
faces the model selection problem.3 The objective of model selection is, of
course, not to better model the training data, but to ensure
that the learned model will generalize to unseen patterns.
Many approaches to this fundamental problem have been
described in the literature. The key objective is always to
prevent the model from becoming too complex, until enough data
has been seen to justify it. The simplest result one might
hope for is to somehow select a single configuration which is
appropriate for the data and problem at hand. Another
solution consists of finding a probability function (or
density) on configuration space. Here ``selection'' becomes a
soft process in which one merely re-weights all of the
possibilities. The first objective is clearly a special case
of the second. In this paper we will ultimately adopt a very simple selection strategy, but, as motivation, first
discuss the problem at a more general level.
Another subtlety associated with the term ``selection'' is
that it seems to imply that the final result is at most as
good as the best individual model. This is not the case. A
blended model can be better than any of its constituents as
shown in the experimental results of
Section 6. A simple example serves to
illustrate this point. Suppose a timid weather-man 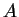 predicts rain and sun each day with equal probability while a
second sure-of-himself weather-man
predicts rain and sun each day with equal probability while a
second sure-of-himself weather-man 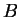 always issues certain
predictions, i.e.
always issues certain
predictions, i.e. 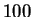 % of rain or
% of rain or 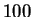 % chance of sun.
Further assume that
% chance of sun.
Further assume that 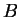 is correct
is correct 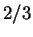 of the time. If the
objective is to maximize the probability assigned to long a
series of trials, then it is easily verified that one
does best by blending their predictions, placing weight
of the time. If the
objective is to maximize the probability assigned to long a
series of trials, then it is easily verified that one
does best by blending their predictions, placing weight 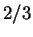 on
on 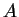 and
and 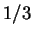 on
on 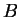 .
.
For simplicity we will assume a discrete setting in which
selection is from among
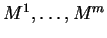 . We seek
non-negative values
. We seek
non-negative values
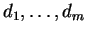 summing to unity, such
that
summing to unity, such
that
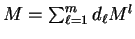 represents a good
choice. Here
represents a good
choice. Here 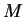 is of course our final model and each
is of course our final model and each
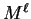 may themselves be complex models such as Gaussian
mixtures. One approach to model selection consists of Bayesian update
in which the starting point is a prior probability function on
the configuration patterns, and after each training example is
predicted by the model, a posterior distribution is computed.
may themselves be complex models such as Gaussian
mixtures. One approach to model selection consists of Bayesian update
in which the starting point is a prior probability function on
the configuration patterns, and after each training example is
predicted by the model, a posterior distribution is computed.
Our purpose in this paper is to explore the basic
effectiveness of the mixture-distance approach so we have
confined ourselves a very simple form of model selection
which amounts to simply using a flat initial prior
and not bothering to update it. That is, we assume all
configurations have equal probability and mix them (average)
accordingly. Bayesian learning and other approaches may be
evaluated in future work.
A first order Gaussian model 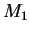 has a diagonal covariance
matrix containing estimates of the individual feature
variances and a mean vector consisting of an estimate of the
distribution's expectation. The second order model
has a diagonal covariance
matrix containing estimates of the individual feature
variances and a mean vector consisting of an estimate of the
distribution's expectation. The second order model 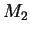 matches
matches 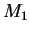 except that its off-diagonal covariance entries
may be non-zero and represent estimates of the feature's
second order statistics. The second order model has of course
many more parameters, so if limited data is available one should
worry about its ability to generalize. Moreover, when forming
Gaussian mixtures, the available data are essentially parceled
out to mixture elements - further exacerbating the problem.
except that its off-diagonal covariance entries
may be non-zero and represent estimates of the feature's
second order statistics. The second order model has of course
many more parameters, so if limited data is available one should
worry about its ability to generalize. Moreover, when forming
Gaussian mixtures, the available data are essentially parceled
out to mixture elements - further exacerbating the problem.
A mixture is just
![$M = (1-f) \cdot M_1 + f \cdot M_2, f \in
[0,1]$](img100.gif) . Consider this mixture generatively where one first
chooses
. Consider this mixture generatively where one first
chooses 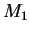 with probability
with probability 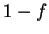 or
or 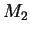 with probability
with probability
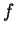 , and then draws a sample at random according to the
selected model. The covariance matrix of the resulting data
vectors is easily seen to be
, and then draws a sample at random according to the
selected model. The covariance matrix of the resulting data
vectors is easily seen to be
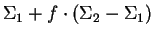 . This is just
. This is just 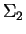 with it's off diagonal
elements multiplied by
with it's off diagonal
elements multiplied by 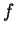 .
.
Now unfortunately 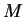 is not necessarily Normally distributed despite
the nature of
is not necessarily Normally distributed despite
the nature of 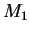 and
and 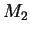 , so we employ the known statistical
expedient in which one approximates a mixture with a single Gaussian.
This leads to the following heuristic which we employ in the experiments
to follow:
The off-diagonal elements of the sample
covariance matrix are multiplied by
, so we employ the known statistical
expedient in which one approximates a mixture with a single Gaussian.
This leads to the following heuristic which we employ in the experiments
to follow:
The off-diagonal elements of the sample
covariance matrix are multiplied by 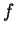 to form a
single Gaussian model which approximately selects
between first and second order statistics.
to form a
single Gaussian model which approximately selects
between first and second order statistics.
This is of course exactly the ML estimate for the parameters of a
single Gaussian trained from the mixed distribution. The
introduction of the 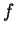 parameter has another practical
benefit. It we require
parameter has another practical
benefit. It we require 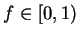 then the resulting
covariance matrix cannot be singular unless some feature has
exactly zero variance. Our experiments will focus on three
natural values:
then the resulting
covariance matrix cannot be singular unless some feature has
exactly zero variance. Our experiments will focus on three
natural values: 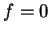 ,
, 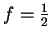 and
and 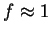 .4 We also point out that
.4 We also point out that 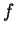 is
employed everywhere in the statistical process including the
maximization step of EM.
is
employed everywhere in the statistical process including the
maximization step of EM.
It is difficult to know a priori how many mixture elements
should be used to describe our database of facial features.
Again there are many approaches to this problem but we adopt
in some sense the simplest by fixing only the upper end
of a range, and mixing all with equal probability.
Experimental Results
To provide a baseline recognition rate to compare our results to, we
applied to simple Euclidean distance metric to the database and
obtained an 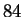 % recognition level.
% recognition level.
For simplicity we adopt a flat selection policy 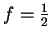 to
decide between first and second order models, i.e. between just the
diagonal variance and the full covariance matrices. Table 2
illustrates how
to
decide between first and second order models, i.e. between just the
diagonal variance and the full covariance matrices. Table 2
illustrates how 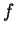 can significantly affect recognition accuracy.
can significantly affect recognition accuracy.
Table 2:
The 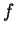 parameter which selects first vs. second order models has
a potent effect on recognizer accuracy.
parameter which selects first vs. second order models has
a potent effect on recognizer accuracy.
|
Mixture |
Recog. Rate |
Recog. Rate |
Recog. Rate |
|
Elements |
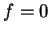 |
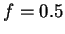 |
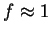 |
|
1 |
93% |
91% |
84% |
|
2 |
86% |
94% |
84% |
|
5 |
88% |
94% |
81% |
|
mixture of |
NA |
95% |
NA |
|
1-10 mixtures |
|
|
|
|
Notice that when the mixture consists of a single Gaussian, a
first order variance model
(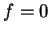 ) is best and the full second order covariance model (
) is best and the full second order covariance model (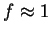 ) is considerably worse.
However, for mixture sizes
) is considerably worse.
However, for mixture sizes 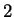 and
and 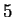 , an off diagonal weighting,
, an off diagonal weighting,
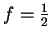 , is best while the full second order model with
, is best while the full second order model with 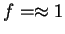 still a distant third. The point of Table 2 is
not that the flat selection model can increase the recognition rate
from
still a distant third. The point of Table 2 is
not that the flat selection model can increase the recognition rate
from 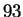 % to
% to 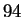 % but rather that the recognition rate is
consistently good using a flat selection, i.e. the recognition rate is
both high and the variation across mixture models is low. A
flat prior is therefore robust and eliminates the uncertainty
associated with any choice of first order variance or second order covariance
models.
% but rather that the recognition rate is
consistently good using a flat selection, i.e. the recognition rate is
both high and the variation across mixture models is low. A
flat prior is therefore robust and eliminates the uncertainty
associated with any choice of first order variance or second order covariance
models.
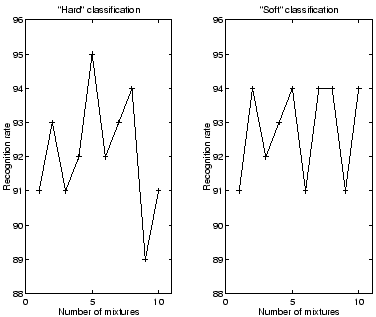
Figure 2:
Recognition accuracy varies considerably with mixture complexity.
Both ``soft'' and ``hard'' VQ versions of mixture distance are presented.
 |
When using a Gaussian mixture model, the number of mixtures present is
often unknown. This is a significant problem since the complexity of
the Gaussian mixture also affects recognizer performance in a
significant and non-monotonic way. This is illustrated by the graphs
of Figure 2 in which models containing 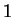 through
through
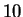 Gaussians were tested. The right graph shows the results using
``soft-VQ'' mixture distance, and the left graph corresponds to
``hard-VQ''.
Gaussians were tested. The right graph shows the results using
``soft-VQ'' mixture distance, and the left graph corresponds to
``hard-VQ''.
Discussing the soft vector quantization method first, we notice that
the peak recognition rate is 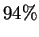 but that the rate varies
considerably as the number of mixture elements changes. Some of this
variation might have been reduced if multiple EM starting points were
used and the recognition results averaged. However, as in the case of
the
but that the rate varies
considerably as the number of mixture elements changes. Some of this
variation might have been reduced if multiple EM starting points were
used and the recognition results averaged. However, as in the case of
the 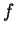 parameter above, our experiments highlight the difficulty of
model selection. To alleviate this, we again propose a flat
stochastic selection scheme, i.e. we assume that each model in the
complexity range
parameter above, our experiments highlight the difficulty of
model selection. To alleviate this, we again propose a flat
stochastic selection scheme, i.e. we assume that each model in the
complexity range 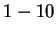 is equally likely and form a mixture of
mixtures. The result is that
is equally likely and form a mixture of
mixtures. The result is that 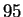 % accuracy is achieved and this
exceeds the performance of any individual model. Once more though,
the significance of this results is not just the improvement in recognition
rate but also the fact that the best recognition rate is achieved
while simultaneously removing the uncertainty associated with mixture
selection.
% accuracy is achieved and this
exceeds the performance of any individual model. Once more though,
the significance of this results is not just the improvement in recognition
rate but also the fact that the best recognition rate is achieved
while simultaneously removing the uncertainty associated with mixture
selection.
The Hard VQ version of mixture-distance is somewhat attractive
if computational cost is an important issue, as described in
Section 4. The left graph of Figure
2 shows its performance which, like the
soft VQ method, is highly variable with mixture complexity. The best
performance 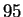 % is attained for
% is attained for 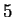 mixture elements and
exceeds the
mixture elements and
exceeds the 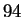 % maximum level of Figure
2. However when a flat mixture of mixtures
was formed as for the soft strategy, performance of
% maximum level of Figure
2. However when a flat mixture of mixtures
was formed as for the soft strategy, performance of 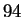 %
resulted. Again, the conclusion to be drawn is that mixtures
of mixtures remove the uncertainty due to variability of recognition
rate with mixture complexity while simultaneously providing excellent
performance.
%
resulted. Again, the conclusion to be drawn is that mixtures
of mixtures remove the uncertainty due to variability of recognition
rate with mixture complexity while simultaneously providing excellent
performance.
Finally we report that limited experiments on the effect
of increasing database size suggest that performance declines
significantly when only a single mixture element is used, and is far
more stable given larger mixtures.
Concluding Remarks
We have demonstrated that the use of a simple form of
mixture-distance, along with a simple solution to the model
selection problem, increase performance on our face
recognition problem from 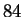 % using Euclidean distance to
% using Euclidean distance to
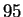 %. This provides strong motivation for careful
consideration when choosing an appropriate metric. A less
impressive but still significant increase from
%. This provides strong motivation for careful
consideration when choosing an appropriate metric. A less
impressive but still significant increase from 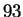 % to
% to
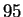 % was observed when we compare the results of a single
first order Gaussian model, with the results using large
mixtures of mixtures. Just as importantly, the recognition
rate is consistently good using a mixture of mixtures and flat
priors on both the order and model selection. In contrast, it
was observed that specific selection of a mixture model and
order statistics can lead to considerable variations in the
recognition rate. The mixture of mixtures is a robust
technique that eliminates this uncertainty. Nevertheless,
further experiments in the face recognition domain and others
will be necessary to evaluate the significance of the
contribution made by generalizing to second order models and
mixtures.
% was observed when we compare the results of a single
first order Gaussian model, with the results using large
mixtures of mixtures. Just as importantly, the recognition
rate is consistently good using a mixture of mixtures and flat
priors on both the order and model selection. In contrast, it
was observed that specific selection of a mixture model and
order statistics can lead to considerable variations in the
recognition rate. The mixture of mixtures is a robust
technique that eliminates this uncertainty. Nevertheless,
further experiments in the face recognition domain and others
will be necessary to evaluate the significance of the
contribution made by generalizing to second order models and
mixtures.
Given the small size of our query database, and our limited
problem domain, it is not possible to conclusively demonstrate
the general effectiveness of the mixture-distance approach.
Nevertheless, our results suggest that  it does lead to
significant improvements over simple Euclidean distance,
it does lead to
significant improvements over simple Euclidean distance,  that flat stochastic selection is an effective solution to
both model selection problems,
that flat stochastic selection is an effective solution to
both model selection problems,  that flat stochastic
selection significantly reduces the otherwise serious
variability of recognition rate with model parameters and
that flat stochastic
selection significantly reduces the otherwise serious
variability of recognition rate with model parameters and
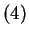 that the hard-VQ algorithm compares well with the
computationally more expensive soft-VQ.
that the hard-VQ algorithm compares well with the
computationally more expensive soft-VQ.
It is also important to realize that the techniques of this
paper are quite independent of the particular feature set we
chose for experimentation. In fact,
mixture-distances can be applied to more direct forms of the image
ranging from raw pixels, through frequency transformations and
the results of principal component and eigenface analyses.
Preliminary work not reported in our experimental results,
included approaches to feature selection based on entropy measures.
We discovered that subsets of our original 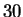 features performed as
well using single Gaussian models. An interesting area for future
work consists of the integration of a feature selection capability
into the full mixture-distance framework.
features performed as
well using single Gaussian models. An interesting area for future
work consists of the integration of a feature selection capability
into the full mixture-distance framework.
In this paper we focused on a very restricted setting in which
only a single example of each face exists in the database. If
instead one assumes the availability of some number of image
pairs corresponding to the same person, the task of estimating
the parameters of our observation process may be
approached more directly. For example, as queries are
processed and assuming the machine receives feedback as to
whether or not its classification is correct, it might adapt
its distance function and one might consider re-formulating
the entire framework into a purely on-line setting. A
significant message of this paper however is that even in the
absence of such feedback, improved distance functions can
be found.
Finally we remark that our feature set will most likely limit
future gains in accuracy. Variations, however small in 3D
pose, camera position and characteristics, and many other
sources of error are not explicitly modeled and should be whenever
possible. However, forming a conceptual framework towards this end is
not nearly as difficult as the associated computational
and optimization issues.
We thank Johji Tajima and Shizuo Sakamoto of NEC Central Laboratories, Sandy
Pentland of the MIT Media Lab, Yael Moses of the Weizmann Institute of
Science, and Jonathon Phillips of the Army Research Laboratory for
providing the databases we used. The authors acknowledge David
W. Jacobs of NEC Research Institute, Sunita L. Hingorani of AT&T Bell
Laboratories, and Santhana Krishnamachari of the University of
Maryland for their participation in this project's predecessor [3] where
portions of Sections 2 and 3 first appeared.
- 1
-
R. J. Baron.
Mechanisms of human face recognition.
Int. J. of Man Machine Studies, 15:137-178, 1981.
- 2
-
R. Brunelli and T. Poggio.
Face recognition: features versus templates.
IEEE Trans. on PAMI, 15(10):1042-1052, 1993.
- 3
-
I. J. Cox, D. W. Jacobs. S. Krishnamachari and P. N. Yianilos.
Experiments on Feature-Based Face Recognition.
NEC Research Institute, 1994.
- 4
-
A. J. Goldstein, L. D. Harmon, and A. B. Lesk.
Identification of human faces.
Proc. of the IEEE, 59(5):748-760, 1971.
- 5
-
L. D. Harmon, M. K. Khan, R. LAsch, and P. F. Ramig.
Machine identification of human faces.
Pattern Recognition, 13:97-110, 1981.
- 6
-
L. D. Harmon, S. C. Kuo, P. F. Ramig, and U. Raudkivi.
Identification of human face profiles by computer.
Pattern Recognition, 10:301-312, 1978.
- 7
-
T. Kanade.
Picture processing System By Computer Complex and Recognition of
Human Faces.
PhD thesis, Kyoto University, 1973.
- 8
-
G. J. Kaufman and K. J. Breeding.
Automatic recognition of human faces from profile silhouettes.
IEEE Trans. on Systems, Man and Cybernetics, SMC-6(2):113-121,
1976.
- 9
-
T. Kanade, Computer Recognition of Human Faces.
Birkhäuser Verlag, Stuttgart Germany, 1977.
- 10
-
Y. Moses, Y. Adini, and S. Ullman.
Face recognition: the problem of compensating for changes in
illumination direction.
In J.-O. Eklundh, editor, Third European Conf. on Computer
Vision, pages 286-296, 1994.
- 11
-
S. J. Nowlan.
Soft Competitive Adaptation: Neural Network Learning Algorithms
based on Fitting Statistical Mixtures.
PhD thesis, School of Computer Science, Carnegie Mellon University,
April 1991.
- 12
-
A. Pentland, B. Moghaddam, and T. Starner.
View-based and modular eigenspaces for face recognition.
In Computer Vision and Pattern Recognition, pages 84-91, 1994.
- 13
-
R. A. Redner and H. F. Walker.
Mixture densities, maximum likelihood and the EM algorithm.
SIAM review, vol. 26, PP. 195-239, 1984.
- 14
-
G. D. Riccia and A. Iserles.
Automatic identification of pictures of human faces.
In 1977 Carnahan Conference on Crime Countermeasures, pages
145-148, 1977.
- 15
-
S. Sakamoto and J. Tajima.
Face feature analysis for human identification.
Technical report, NEC Central Research Laboratory, 1994.
- 16
-
J. Shepherd and H. Ellis.
Face recognition and recall using computer-interactive methods with
eye witnesses.
In Processing Images of Faces, editor, V. Bruce
and H. Burton, Ablex Publishing, 1992.
- 17
-
M. A. Turk and A. P. Pentland.
Face recogntion using eigenfaces.
In IEEE Int. Conf. on Computer Vision and Pattern Recognition,
pages 586-591, 1991.
- 18
-
S. White.
Features in face recognition algorithms.
Part of the Area Exam for Area II Course VI, MIT, February 1992.
- 19
-
J. Tojima and S. Sakamoto.
Private Communication.
1994.
- 20
-
L. Xu and M. I. Jordan.
On convergence properties of the em algorithm for gaussian mixtures.
Technical Report A.I. Memo No. 1520, Massachusetts Institute of
Technology, Artificial Intelligence Laboratory, January 1995.
- 21
-
P. N. Yianilos.
Metric learning via normal mixtures.
Technical report, The NEC Research Institute, Princeton, New Jersey,
1995.
Feature-Based Face Recognition Using Mixture-Distance
This document was generated using the
LaTeX2HTML translator Version 2K.1beta (1.47)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -image_type gif -nonext_page_in_navigation -noprevious_page_in_navigation -up_url ../main.html -up_title 'Publication homepage' -numbered_footnotes faces.tex
The translation was initiated by Peter N. Yianilos on 2002-06-30
Footnotes
- ... Yianilos1
-
The first and third authors are with NEC
Research Institute, 4 Independence Way,
Princeton, NJ 08540. The second is with the
University of Montreal, Department of Computer
Science. Direct Email to the third author at
pny@research.nj.nec.com. This manuscript
was completed during October 1995.
- ... below2
- Selection was
necessary only because many of the available images were not frontal
views.
- ... problem.3
- Formally, the
configuration of a parameterized model is just an extension of
its parameters.
- ....4
- We use
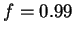 .
.
Up: Publication homepage
Peter N. Yianilos
2002-06-30