Eric S. Ristad - Peter N. Yianilos
Research Report1 CS-TR-541-96
December, 1996
(Revised November, 1997)
We expose a fundamental degeneracy in the relationship between a normal mixture and the a posteriori class probability functions that it induces, and use this degeneracy to prove that reweighting a dataset can almost always give rise to a normal mixture that exhibits any desired class function behavior. This establishes that EM-style approaches are sufficiently expressive for a posteriori optimization problems and opens the way to the design of new algorithms for them.
Keywords:Expectation Maximization (EM), Normal Mixtures, Gaussian Mixtures, Supervised Learning, Maximize Mutual Information (MMI).
A finite normal mixture is a stochastic combination of normal
densities. That is, a probability density function ![]() on
on
![]() of
the form
of
the form
![]() where
where
![]() with
with
![]() , and
, and
![]() denotes the normal density with mean
denotes the normal density with mean ![]() and covariance
and covariance ![]() . Each constituent normal density is
referred to as a component of the mixture, and
. Each constituent normal density is
referred to as a component of the mixture, and
![]() are the mixing coefficients. Normal mixtures have proven useful
in several areas including pattern recognition
[4] and speech recognition
[6,2,5] - along with vector quantization and many
others.
are the mixing coefficients. Normal mixtures have proven useful
in several areas including pattern recognition
[4] and speech recognition
[6,2,5] - along with vector quantization and many
others.
The problem of finding a ![]() -component normal mixture
-component normal mixture ![]() that maximizes the likelihood
that maximizes the likelihood
![]() .
of an unlabeled dataset
.
of an unlabeled dataset
![]() may be approached using the well-known expectation maximization (EM)
algorithm [1,3,7]. EM iteratively
re-weights each sample's membership in each of the
may be approached using the well-known expectation maximization (EM)
algorithm [1,3,7]. EM iteratively
re-weights each sample's membership in each of the ![]() mixture
components by the posteriori probability
of the components given the sample.
mixture
components by the posteriori probability
of the components given the sample.
Normal mixtures are also applied to pattern classification problems.
For classification problems,
each mixture component may be thought of as corresponding to a pattern
class. Given a class
label ![]() for each element
for each element ![]() in our dataset, we would
like to maximize
in our dataset, we would
like to maximize
![]() . Here the goal is to
optimize the mixture's a posteriori performance, that is to
predict the correct labels, not model the observation vectors
themselves. This is sometimes called the maximum mutual
information (MMI) criterion in the speech recognition literature
[2] and may be viewed as probabilistic supervised learning.
. Here the goal is to
optimize the mixture's a posteriori performance, that is to
predict the correct labels, not model the observation vectors
themselves. This is sometimes called the maximum mutual
information (MMI) criterion in the speech recognition literature
[2] and may be viewed as probabilistic supervised learning.
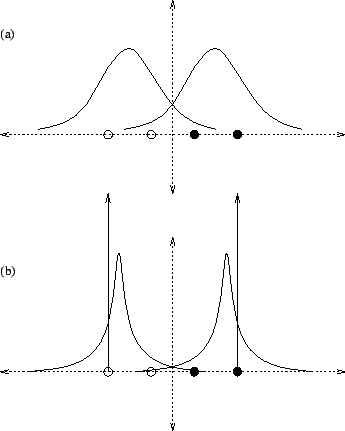
A naive algorithm for this problem segregates the data elements by class, constructs the maximum-likelihood normal density for each class, and combines the resulting densities to form a mixture. This approach can be far from optimal, as illustrated by figure 1. Part (a) of the figure depicts the maximum-likelihood normal densities corresponding to the pair of points in each class. These densities are specified by the unweighted sample mean and unweighted sample covariance of each class in isolation. Although the resulting mixture maximizes the probability of the samples, it does not maximize the conditional probability of the classes given the samples. For example, the density shown in part (b) assigns greater conditional probability to the classes given the samples, although it assigns less probability to the samples themselves. To accomplish this, increased weight is assigned to the outermost two points in part (b). In this example the classes neatly divide and the optimal densities have zero-variance corresponding to placing all of the emphasis on a single element of each class. We view these weights as placing emphasis on the dataset, resulting in a modified collection of normal densities.
 |
The question that motivates this paper is then:
Does there exist an EM-style algorithm for the a posteriori maximization of normal mixtures?By ``EM-style'' we mean an iterative algorithm that operates by varying the emphasis placed on a dataset rather than by viewing the model's natural parameters as variables in the optimization.
One might certainly imagine one based perhaps on the common machine learning heuristic where one increases the weight of a mistake in order to improve classification accuracy - a technique sometimes referred to as corrective training. But it is not at all clear that emphasis algorithms have the expressive power to discover the solution. The convex reweighting performed by EM cannot, for example, generate a mean vector outside of the dataset's convex hull.
This paper takes the first step towards such an algorithm by bringing the expressive power of emphasis schemes more clearly into focus. Section 2 defines two normal mixtures to be class equivalent if they induce identical a posteriori class functions, i.e. perform identically as probabilistic classifiers. It is shown there that the relationship between mixtures and their class behavior is highly degenerate, and theorem 1 characterizes this degeneracy in a way that is useful for our objective. As a positive result of this degeneracy one can search the entire space of class functions without considering all possible mixtures. So to solve the a posteriori maximization problem above, it suffices to express any normal mixture that induces optimal class functions. We are then led to ask:
When can emphasis of an observation set induce a mixture that is class equivalent to an arbitrary one?Obviously the observation set must satisfy certain orthodoxy conditions such as being of sufficient size and possessing in some sense enough independence. But beyond these issues the fact that many mean vectors and covariance matrices are not expressible by emphasis would seem to present a much larger obstacle.
A positive answer to this question is given by theorem 2 of section 3. It states that one can almost always exactly match the a posteriori behavior of an arbitrary mixture by an emphasis method that slightly modifies the EM approach. Therefore any optimization problem that depends only on a mixture's induced class functions can be solved using this form of emphasis.
We conclude our introduction by reviewing EM and presenting our view of it as an emphasis reparameterization scheme.
Let
![]() be a set of observations. Any set of
positive weights
be a set of observations. Any set of
positive weights
![]() , gives rise in a natural way to a
normal density. That is, the normal density having mean:
, gives rise in a natural way to a
normal density. That is, the normal density having mean:
The well known expectation maximization (EM) method may be viewed as a process which accepts as input a normal mixture, and outputs an emphasis parameter set - from which an improved normal mixture arises. This cycle continues as the algorithm climbs towards a local maximum, which is a stationary point of the iteration. The global maximum is also stationary point.
More precisely, Given data values
![]() and a normal
mixture
and a normal
mixture ![]() , one begins by computing
, one begins by computing
![]() . Conceptually the result is a
. Conceptually the result is a ![]() table of nonnegative values. The rows of this table are
then normalized so that their sum is one. Each row then corresponds
to a convex combination of the samples. The entries along a row are
thought of as weights attributed to the sample. Each improved
mean vector
table of nonnegative values. The rows of this table are
then normalized so that their sum is one. Each row then corresponds
to a convex combination of the samples. The entries along a row are
thought of as weights attributed to the sample. Each improved
mean vector ![]() is merely the corresponding weighted average
(convex combination) of the sample vectors. Each improved covariance
is the sample convex combination of outer products
is merely the corresponding weighted average
(convex combination) of the sample vectors. Each improved covariance
is the sample convex combination of outer products
![]() . The improved mixing parameters are obtained by
normalizing the vector consisting of the table row weights prior to
their normalization. This process is repeated in an elegant cycle,
i.e. each table induces a mixture that gives rise to a new table, and
so on.
. The improved mixing parameters are obtained by
normalizing the vector consisting of the table row weights prior to
their normalization. This process is repeated in an elegant cycle,
i.e. each table induces a mixture that gives rise to a new table, and
so on.
From our viewpoint, what is interesting here is that it is possible to
search for an optimal normal mixture, by searching over the space of
values for the ![]() emphasis parameters - rather than using
the canonical parameterization consisting of the unknown
mean vectors, covariance matrices, and mixing coefficients.
emphasis parameters - rather than using
the canonical parameterization consisting of the unknown
mean vectors, covariance matrices, and mixing coefficients.
Only a locally optimal solution is found through EM but it is important to realize that the global optimum is a stationary point of the iteration. This means that it can be expressed via emphasis, i.e. that there exists a table which induces the globally optimal mixture. This is interesting because not all mixtures can be induced from the table. In particular, as noted earlier, the induced means must lie within the convex hull of the sample set, and the covariances are similarly constrained.
This section illuminates certain fundamental aspects of the nature of normal mixtures. Thinking of each mixture component as a class, we focus on the corresponding a posteriori class probability functions. It is shown that the relationship between these functions and the mixture's parameters, is highly degenerate - and that the precise nature of this degeneracy leads to somewhat unusual and counter-intuitive behavior. Even complete knowledge of a mixture's a posteriori class behavior, reveals essentially nothing of its absolute nature, i.e. mean locations and covariance norms. Consequently a mixture whose means are located in a small ball anywhere in space, can project arbitrary class structure everywhere in space.
 |
A convenient visualization of class functions, focuses on decision boundaries, i.e. the surfaces along which classification is ambiguous. Imagery like ours in figure 2, and pages 28-31 of [4], suggest an intuitive relationship between mixture component locations, and the resulting a posteriori class structure and decision surfaces. One imagines each mean to be asserting ownership over some volume of space surrounding it. This view is however far from the truth and our theorem 1 reveals that the a posteriori class behavior of normal mixtures is far stranger and counter-intuitive than is generally understood. It shows that knowledge of a mixture's a posteriori class structure (which may be thought of as decision surfaces), tells us essentially nothing about the absolute location of the mixture's means - or the absolute nature of its covariances. One can easily imagine a normal mixture, and picture its corresponding class structure. Now if one is instead given only this class structure, the theorem says that infinitely many normal mixtures are consistent with it - and in particular that the means of such a mixture can be located within an arbitrarily small ball, located anywhere in space.
Despite the popularity and significant role of normal mixtures in statistical modeling and pattern recognition, the precise nature of this fascinating and highly degenerate relationship between class functions and mixtures has received little attention. Part of the reason may be that the simple view in which component means dominate some portion of the space around them is exactly the case when all covariances have identical determinant, and uniform mixing coefficients are used. The most common example of this setting consists of nearest-neighbor Euclidean clustering which corresponds to the identity covariance case. In practice, if the determinants are somewhat comparable, and the mixing coefficients nearly uniform, the simple view is almost always valid. But in many cases, such as when mixture parameters are estimated using an optimization procedure, no such constraint is imposed, and the means, covariance matrices, and mixing coefficients are free to assume any values. Here the full range of strange behavior may be expected.
We now turn to the section's main mathematical development. Examples and discussion follow and the section ends with a technical convergence-rate result that is needed to establish the next sections' main result.
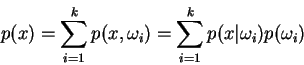
where the constants
![]() are referred to as the
mixing coefficients. Any such mixture induces
are referred to as the
mixing coefficients. Any such mixture induces ![]() a posteriori
class functions:
a posteriori
class functions:
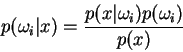
Two finite mixtures are class-equivalent if they induce the same class functions.
The class functions are not independent since they are constrained by:
![]() . We begin with a simple proposition, which
allows us in what follows to focus on ratios of conditional
probabilities, and ignore constant factors. This will be important
since the nonconstant portion of the ratio of two normal densities is
a rather simple object.
. We begin with a simple proposition, which
allows us in what follows to focus on ratios of conditional
probabilities, and ignore constant factors. This will be important
since the nonconstant portion of the ratio of two normal densities is
a rather simple object.
then there exist mixing coefficients
![]() such that the resulting mixture
such that the resulting mixture ![]() is
class-equivalent to
is
class-equivalent to ![]() .
.
proof: We begin by giving a formula for mixing coefficients
![]() , such that:
, such that:
Relaxing for the moment the restriction
![]() , observe that if
, observe that if ![]() were
were ![]() , then setting
, then setting
![]() ,
would satisfy the equation. Normalization then yields a
solution which does sum to
,
would satisfy the equation. Normalization then yields a
solution which does sum to ![]() :
:
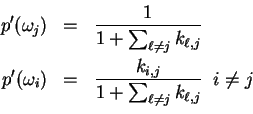
Multiplying each side of Eq. 4 by the corresponding side of Eq. 3 yields:
The approach above works so long as
![]() . If it is zero,
then
. If it is zero,
then ![]() may be treated as a
may be treated as a ![]() component mixture, and the proposition
follows by induction.
Till now
component mixture, and the proposition
follows by induction.
Till now ![]() has been fixed and Eq. 5 is
established for
has been fixed and Eq. 5 is
established for ![]() . This equation is however easily
extended to any pair
. This equation is however easily
extended to any pair ![]() of indices. Let
of indices. Let ![]() denote
denote
![]() and
and ![]() denote
denote
![]() . Then:
. Then:
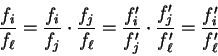
Now we may write:
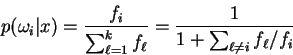
and a corresponding expression for
![]() in terms of
in terms of
![]() . We have already seen that all ratios
. We have already seen that all ratios
![]() , so
, so
![]() whence
whence
![]() and we are done.
and we are done.![]()
We now specialize our discussion to mixtures whose components are normal densities.
The mixture's parameters are then
![]() .
.
The following theorem exposes the large degeneracy in the relationship between normal mixtures, and their induced class functions.
where
![]() refers to the
Frobenius/Euclidean matrix norm.
refers to the
Frobenius/Euclidean matrix norm.
proof: Begin by selecting some distinguished component ![]() .
By proposition 1
we have only to produce
.
By proposition 1
we have only to produce
![]() and
and
![]() such that the ratio conditions of the proposition are satisfied.
Since constant factors do not matter, we ignore several portions of the
definition of a normal density Eq. 6. Namely, the leading constant
and the constant portion of the exponent once multiplied out. The result is that:
such that the ratio conditions of the proposition are satisfied.
Since constant factors do not matter, we ignore several portions of the
definition of a normal density Eq. 6. Namely, the leading constant
and the constant portion of the exponent once multiplied out. The result is that:
The proportional ratio condition of proposition 1 then leads immediately to the following necessary and sufficient conditions:
We set
![]() and begin by sketching the rest of the proof. The
constraints are satisfied by choosing
and begin by sketching the rest of the proof. The
constraints are satisfied by choosing
![]() so that each of
its eigenvalues is large. Each resulting
so that each of
its eigenvalues is large. Each resulting
![]() must
then be positive definite and will also have large eigenvalues. Both
must
then be positive definite and will also have large eigenvalues. Both
![]() and
and
![]() then have small norm, satisfying the
requirements of the theorem. In this process, it is only
then have small norm, satisfying the
requirements of the theorem. In this process, it is only
![]() we are free to choose. Each choice determines the
we are free to choose. Each choice determines the
![]() , and
, and
![]() (since we have already set
(since we have already set
![]() ). In
the limit, as we choose
). In
the limit, as we choose
![]() with increasingly large
eigenvalues,
with increasingly large
eigenvalues,
![]() approaches zero
whence we can satisfy the theorem's other condition.
approaches zero
whence we can satisfy the theorem's other condition.
Denote by
![]() the largest eigenvalue of positive definite matrix
the largest eigenvalue of positive definite matrix ![]() , and by
, and by
![]() the smallest. For matrices
the smallest. For matrices ![]() , it then follows easily from
the Cauchy-Schwartz inequality that
, it then follows easily from
the Cauchy-Schwartz inequality that
![]() , by writing
, by writing
![]() where
where ![]() denotes any unit length vector.
Now the first constraint in Eq. 7 may be written:
denotes any unit length vector.
Now the first constraint in Eq. 7 may be written:
and we then have:
The parenthesized term is constant since we are given both
![]() and
and ![]() , and by subadditivity of symmetric
matrix spectral radii, does not exceed their sum
, and by subadditivity of symmetric
matrix spectral radii, does not exceed their sum
![]() . We can easily choose
. We can easily choose
![]() such
that
such
that
![]() is arbitrarily large, e.g.
is arbitrarily large, e.g. ![]() where
where ![]() is a large positive constant. It follows then that
is a large positive constant. It follows then that
![]() will also be arbitrarily large, ensuring that
it is positive definite.
will also be arbitrarily large, ensuring that
it is positive definite.
Next recall that the column norms of a matrix ![]() cannot exceed its
spectral radius (operate on each member of the canonical basis). In
our positive definite setting each is then bounded above by
cannot exceed its
spectral radius (operate on each member of the canonical basis). In
our positive definite setting each is then bounded above by
![]() , so that
, so that
![]() . Choosing the
smallest eigenvalue of
. Choosing the
smallest eigenvalue of
![]() and
and
![]() to be
arbitrarily large, forces
to be
arbitrarily large, forces
![]() and
and
![]() to
be arbitrarily small - satisfying the theorem's first condition.
to
be arbitrarily small - satisfying the theorem's first condition.
We set
![]() to be equal to
to be equal to ![]() from the statement of the theorem,
and the second constraint in Eq. 7 may be rearranged to yield:
from the statement of the theorem,
and the second constraint in Eq. 7 may be rearranged to yield:
By our earlier discussion, we may force
![]() to be arbitrarily
close to zero - forcing the bracketed term in Eq. 9 to approach zero
as well. We next show that the first parenthesized term
to be arbitrarily
close to zero - forcing the bracketed term in Eq. 9 to approach zero
as well. We next show that the first parenthesized term
![]() tends to the identity matrix
tends to the identity matrix ![]() as
as
![]() .
This then demonstrates that
.
This then demonstrates that
![]() satisfying the theorem's
second condition, and finishes the proof.
satisfying the theorem's
second condition, and finishes the proof.
It is easy to see that
![]() if and only if
if and only if
![]() .
Using Eq. 8 this becomes:
.
Using Eq. 8 this becomes:
which is clearly the case since
![]() .
.![]()
To recapitulate, any location for
![]() , and sufficiently large (in
the
, and sufficiently large (in
the
![]() sense)
sense)
![]() , will give rise using the proof's
constructions, to values for the other means, covariances, and mixture
coefficients, such that a class-equivalent mixture results.
The proof goes on to establish that in the limit, everything is
confined as required within an
, will give rise using the proof's
constructions, to values for the other means, covariances, and mixture
coefficients, such that a class-equivalent mixture results.
The proof goes on to establish that in the limit, everything is
confined as required within an ![]() -neighborhood.
-neighborhood.
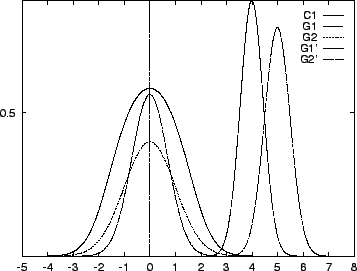 |
Figure 3 provides a simple one dimensional example of
the normal mixture to class function degeneracy. The left pair of
Gaussians G1,G2 both have zero mean. The taller one, G1
corresponds to the first class and has variance ![]() , while G2
has variance 1 and corresponds to the second class. When mixed
evenly, the a posteriori probability C1 results. Notice
that C1 assumes value
, while G2
has variance 1 and corresponds to the second class. When mixed
evenly, the a posteriori probability C1 results. Notice
that C1 assumes value ![]() where G1 crosses G2.
The right pair of Gaussians G1',G2' have means at
where G1 crosses G2.
The right pair of Gaussians G1',G2' have means at ![]() and
and ![]() ,
and variances of
,
and variances of ![]() and
and ![]() respectively. An even mixture of
them would result in a class function very different from C1.
But if very little weight (
respectively. An even mixture of
them would result in a class function very different from C1.
But if very little weight (
![]() ) is placed on
G1', its mode drops under the graph of G2', and surprisingly,
the induced class function is exactly C1. The parameters of
this new mixture follow immediately from the calculations within
the proof of theorem 1.
) is placed on
G1', its mode drops under the graph of G2', and surprisingly,
the induced class function is exactly C1. The parameters of
this new mixture follow immediately from the calculations within
the proof of theorem 1.
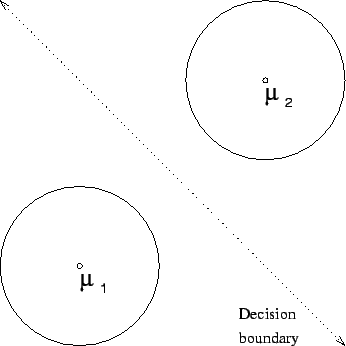
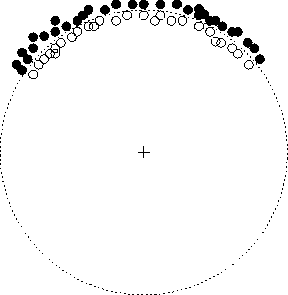
Figure 4 depicts another two class problem, this time in
two dimensions. Here various elements of each class are arranged so
that they may be perfectly separated by a circular decision boundary.
It is clear that we can create such a boundary by modeling each class
with a normal density centered at the origin. We may evenly mix these
components and set their covariance matrices to be multiples of the
identity matrix; chosen so that the two density's intersection is the
desired circle. This is in some sense the canonical solution but
infinitely many others are possible. To begin with, it is not necessary that
both covariance matrices be multiples of the identity. It suffices
that their difference be such a multiple. It is not necessary that
their means be located at the origin. Given a choice of covariance
matrices, and the location of one mean, a location for the other may
be computed which gives rise to the same boundary. Moreover, by
choosing the covariances to be nearly zero, corresponding to highly
peaked densities, the two means may be located within an arbitrary
![]() -neighborhood anywhere in
-neighborhood anywhere in
![]() . This illustrates the
degeneracy by focusing only on the decision boundary, but theorem
1 shows that the family of class functions may be
matched everywhere. The situation in figure 4 was first
contrived in an attempt to disprove our emphasis
reparameterization theorem, the subject to which we next turn. The
data points are arranged along only part of the circle so that no
convex combination of them, can possibly express the origin. That is,
the origin is outside of the convex hull of the dataset. At that time
we thought that this would prevent such combinations from leading to a
mixture capable of inducing the desired circular decision boundary.
The revelation of theorem 1 is that the component
means of such a mixture can be located anywhere.
. This illustrates the
degeneracy by focusing only on the decision boundary, but theorem
1 shows that the family of class functions may be
matched everywhere. The situation in figure 4 was first
contrived in an attempt to disprove our emphasis
reparameterization theorem, the subject to which we next turn. The
data points are arranged along only part of the circle so that no
convex combination of them, can possibly express the origin. That is,
the origin is outside of the convex hull of the dataset. At that time
we thought that this would prevent such combinations from leading to a
mixture capable of inducing the desired circular decision boundary.
The revelation of theorem 1 is that the component
means of such a mixture can be located anywhere.
 |
We have seen that all the
![]() converge to
converge to
![]() as the
latter tends to zero. At the same time, the
as the
latter tends to zero. At the same time, the
![]() approach
approach
![]() . The rate of convergence is our next topic. In particular
we will show that
. The rate of convergence is our next topic. In particular
we will show that
![]() quadratically as
quadratically as
![]() . This is formalized in the
following proposition which is needed to establish the main result of
the next section. We remark that the convergence of each
. This is formalized in the
following proposition which is needed to establish the main result of
the next section. We remark that the convergence of each
![]() to
to
![]() is only linear.
is only linear.
proof: The difference
![]() is
constant and is denoted by
is
constant and is denoted by ![]() . Then:
. Then:
Denoting
![]() as
as ![]() for clarity this becomes:
for clarity this becomes:
Now clearly
![]() with
with
![]() and
the eigenvalues of
and
the eigenvalues of ![]() approach unity at this rate.
So
approach unity at this rate.
So
![]() as well - also with
as well - also with
![]() .
Hence
.
Hence
![]() in Eq. 10.
But
in Eq. 10.
But
![]() as well, so
as well, so
![]() .
.![]()
The question ``Can emphasis induce a mixture class-equivalent to an arbitrary one?'' posed at the beginning of this paper is reasonable since from theorem 1 we know that the means of such a mixture can lie within an arbitrarily small ball located anywhere in space. So confinement to the convex hull of the samples is not necessarily a restriction. Likewise the covariances can be chosen to have arbitrarily small Frobenius norm.
The main result of this section is a qualified positive answer to this question. It states that a modified form of emphasis can, for almost all sufficiently large observation sets, induce a mixture which is class equivalent to an arbitrary one.
Modifications are needed because even though the means and covariances may be chosen with a great deal of freedom, they are still highly constrained by the conditions of Eq. 7 - and it is sometimes impossible to generate a mixture which has satisfies these constraints by the form of emphasis employed by EM. The next section expands on the limits of strict EM-style emphasis.
The required modifications consist of a single change to Eq. 2 which becomes:
where the leading normalization has been removed. This allows the scale of the covariance to be adjusted without affecting the mean.
Before stating and proving our reparameterization result, a particular matrix is defined whose nonsingularity is a condition of the theorem.
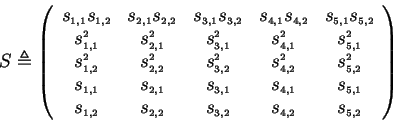
Our condition is that ![]() be nonsingular.
be nonsingular.
It is not hard to show that this condition is almost always satisfied, a fact formalized by:
proof: Since the matrix consists of monomials of distinct structure,
no non-zero linear combination (over the ring of polynomials)
of its columns or rows vanishes. So its determinant, as a
polynomial, is not identically zero. But the roots of a
non-zero polynomial form a set of zero measure.
![]()
Next we simplify our setting, adjust notation, and establish one more
proposition before turning to the theorem.
Without loss of generality, we may assume that our samples have mean
zero. To see this, first let ![]() denote some target mean, where we
seek stochastic
denote some target mean, where we
seek stochastic ![]() values such that
values such that
![]() .
We may equivalently solve
.
We may equivalently solve
![]() ,
where
,
where
![]() and
and
![]() ,
since
,
since
![]() . The
problem of expressing a target covariance is unchanged by coordinate
translation, since
. The
problem of expressing a target covariance is unchanged by coordinate
translation, since
![]() . Notice that
this is true even if the
. Notice that
this is true even if the ![]() are not stochastic. So in what
follows, we will drop the prime notation and simply assume that
are not stochastic. So in what
follows, we will drop the prime notation and simply assume that
![]() .
.
The mixture we generate will have all of its means located near zero,
the mean of the sample set. The distinguished mixture component,
identified with index ![]() in the previous section, is located exactly
at the origin. The location of the other mean vectors, are thought of
as small displacements
in the previous section, is located exactly
at the origin. The location of the other mean vectors, are thought of
as small displacements ![]() from the origin. We then write
from the origin. We then write
![]() to mean
to mean ![]() , and the
, and the ![]() matrix is then
parameterized by
matrix is then
parameterized by ![]() in the obvious way, and denoted
in the obvious way, and denoted ![]() .
Note that
.
Note that ![]() is just
is just ![]() as originally defined.
as originally defined.
proof: Immediate from the continuity of the ![]() parameterization of
parameterization of ![]() .
.
![]()
Each value of ![]() corresponds to a choice of mean vector, and
gives rise to a linear mapping
corresponds to a choice of mean vector, and
gives rise to a linear mapping ![]() . That is, for each choice
of
. That is, for each choice
of ![]() , a linear map arises. The proposition tells us that so
long as our mixture's means are kept within distance
, a linear map arises. The proposition tells us that so
long as our mixture's means are kept within distance ![]() of the
origin, all associated linear mappings are invertible.
of the
origin, all associated linear mappings are invertible.
The utility of ![]() is that it allows us to simultaneously
express the objectives of obtaining by emphasis a specified mean vector, and
covariance matrix. If
is that it allows us to simultaneously
express the objectives of obtaining by emphasis a specified mean vector, and
covariance matrix. If ![]() is a nonnegative emphasis vector,
is a nonnegative emphasis vector,
![]() is the targeted mean vector, and
is the targeted mean vector, and ![]() the desired
covariance matrix, then we must solve the system
the desired
covariance matrix, then we must solve the system
![]() . Here
. Here ![]() is regarded as a vector which is
concatenated (denoted ``:'') with the d-dimensional zero vector.
is regarded as a vector which is
concatenated (denoted ``:'') with the d-dimensional zero vector.
The ![]() above is nonnegative, but not necessarily stochastic.
This may seem to be inconsistent with our definition of the generation
of a mean vector by emphasis, because of the normalization it
includes. But it is not since
above is nonnegative, but not necessarily stochastic.
This may seem to be inconsistent with our definition of the generation
of a mean vector by emphasis, because of the normalization it
includes. But it is not since
![]() is
equivalent to
is
equivalent to
![]() , which is
exactly our definition.
, which is
exactly our definition.
Also, the number of parameters may be reduced to
![]() , matching the complexity of the canonical
parameterization, by replacing the top
, matching the complexity of the canonical
parameterization, by replacing the top ![]() -table row, by
a single new parameter
-table row, by
a single new parameter ![]() .
.
proof: Choose some subset of the ![]() of size exactly
of size exactly ![]() that satisfies condition 1. We disregard the
other elements entirely, and therefore simply assume that
that satisfies condition 1. We disregard the
other elements entirely, and therefore simply assume that ![]() .
As argued earlier, we may also assume without loss of
generality that the
.
As argued earlier, we may also assume without loss of
generality that the ![]() have mean zero. Then the
distinguished mixture component from theorem
1, with parameters
have mean zero. Then the
distinguished mixture component from theorem
1, with parameters
![]() , is chosen as follows. Its mean
, is chosen as follows. Its mean
![]() is the
origin, and its covariance
is the
origin, and its covariance
![]() is proportional to the
average of the element self-outer-products, i.e.:
is proportional to the
average of the element self-outer-products, i.e.:
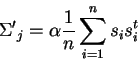
This may be thought of as choosing the first row of the
![]() table to be
table to be ![]() , and introducing a new scale
parameter
, and introducing a new scale
parameter ![]() . The table's top row elements are no
longer parameters, so the total becomes
. The table's top row elements are no
longer parameters, so the total becomes ![]() table
parameters, plus
table
parameters, plus ![]() mixing parameters, plus
mixing parameters, plus ![]() -
matching the count in the statement of the theorem. As
described in the proof of theorem 1, the
choice of
-
matching the count in the statement of the theorem. As
described in the proof of theorem 1, the
choice of
![]() is arbitrary, but
is arbitrary, but
![]() may need to
be scaled down to preserve the positive nature of all
matrices. The number of resulting parameters in a direct
parameterization (i.e. consisting of means, covariances, and
mixing parameters), then matches our count.
may need to
be scaled down to preserve the positive nature of all
matrices. The number of resulting parameters in a direct
parameterization (i.e. consisting of means, covariances, and
mixing parameters), then matches our count.
As
![]() we know that the
we know that the
![]() . Our first step is to choose
. Our first step is to choose ![]() sufficiently small, so that the largest
sufficiently small, so that the largest
![]() is
smaller than the
is
smaller than the ![]() of proposition 4.
Next,
of proposition 4.
Next, ![]() is possibly reduced further until each
covariance matrix
is possibly reduced further until each
covariance matrix
![]() arising from Eq. 4
is positive.
arising from Eq. 4
is positive.
Each ![]() corresponds to a
corresponds to a ![]() value in our definition
of
value in our definition
of ![]() . The reference mean, located at the origin,
corresponds to
. The reference mean, located at the origin,
corresponds to ![]() , and by our construction, arises
from weighting the
, and by our construction, arises
from weighting the ![]() by non-negative
by non-negative ![]() values -
in this case uniform ones. Associated with each
values -
in this case uniform ones. Associated with each
![]() there
is also a
there
is also a
![]() . Recall from our earlier discussion, that
our focus is on the equation
. Recall from our earlier discussion, that
our focus is on the equation
![]() . Since
. Since ![]() is non-singular for each of the
is non-singular for each of the
![]() , we know that some vector of
, we know that some vector of ![]() values
satisfies this equation. We have only to show that
solutions consisting only of nonnegative values can be found.
values
satisfies this equation. We have only to show that
solutions consisting only of nonnegative values can be found.
We will say than a point is representable under some
![]() , if its inverse image under this mapping consists
only of non-negative values.
There exists a representable open neighborhood about
, if its inverse image under this mapping consists
only of non-negative values.
There exists a representable open neighborhood about
![]() under
under ![]() , since the inverse image
of this point2 is the constant vector
, since the inverse image
of this point2 is the constant vector
![]() , and consists of strictly positive values.
, and consists of strictly positive values.
Within our bounds on ![]() , it
uniform-continuously3 parameterizes
, it
uniform-continuously3 parameterizes ![]() . Hence there
exist values
. Hence there
exist values ![]() and
and ![]() , such that for all
, such that for all
![]() with
with
![]() , the open ball about
, the open ball about
![]() , with radius
, with radius ![]() , is
representable under
, is
representable under ![]() . To avoid introducing another
symbol, let
. To avoid introducing another
symbol, let ![]() now denote the maximum such
radius.4
now denote the maximum such
radius.4
Next notice that the space of representable points is convex and
includes the origin. So representability of
![]() implies representability for all
implies representability for all ![]() values.
Now if necessary, reduce
values.
Now if necessary, reduce ![]() further so that all the
further so that all the
![]() are within
are within ![]() of the origin.
of the origin.
Now let ![]() denote the subspace of nonnegative
denote the subspace of nonnegative ![]() vectors.
Let:
vectors.
Let:

Subspace ![]() is the portion of the range, representable under
any
is the portion of the range, representable under
any ![]() such that
such that
![]() .
.
About
![]() we have seen that there is a
representable ball of radius
we have seen that there is a
representable ball of radius ![]() which touches the boundary
of
which touches the boundary
of ![]() . We now denote this radius by
. We now denote this radius by
![]() since we
are about to consider its behavior as
since we
are about to consider its behavior as
![]() .
By our earlier comments,
.
By our earlier comments, ![]() includes
includes
![]() , and all proportional vectors, in particular as
, and all proportional vectors, in particular as
![]() .
.
The geometric observation key to our proof is that
![]() can shrink only as fast as
can shrink only as fast as ![]() itself,
since this value represents the shortest distance to some
point set, in this case
itself,
since this value represents the shortest distance to some
point set, in this case ![]() . We imagine
. We imagine ![]() to be a tunnel, leading to the origin while constricting, with
the boundary of
to be a tunnel, leading to the origin while constricting, with
the boundary of ![]() forming the tunnel's wall.
forming the tunnel's wall.
Focus now on some
![]() . While there is a corresponding
representable ball about
. While there is a corresponding
representable ball about
![]() of radius
of radius
![]() , there is no guarantee that
, there is no guarantee that
![]() is
within it.
As
is
within it.
As
![]() , we have seen that the radius of
this ball shrinks linearly with
, we have seen that the radius of
this ball shrinks linearly with ![]() .
But the distance of
.
But the distance of
![]() from
from
![]() by
proposition 2 shrinks quadratically with
by
proposition 2 shrinks quadratically with ![]() ,
whence eventually, i.e. for small enough
,
whence eventually, i.e. for small enough ![]() ,
,
![]() becomes representable.
Then
becomes representable.
Then ![]() is reduced as necessary for for each component
of the mixture, so that afterwards, every
is reduced as necessary for for each component
of the mixture, so that afterwards, every
![]() is
representable.
is
representable.![]()
Other emphasis theorems are possible. In particular it is much easier
to establish a similar result in which the weights may be either
positive or negative because then the only requirement is that ![]() be nonsingular.
be nonsingular.
In the previous section we saw that using a particular form of emphasis reparameterization, the a posteriori behavior of any mixture could be matched. We say that such a sample set and emphasis method is universal. This section is by contrast essentially negative, and begins with an example demonstrating that even in one dimension, strict EM-style emphasis is not universal.
Our example is in
![]() , and includes two observation
points located at
, and includes two observation
points located at ![]() and
and ![]() . The leading normalization
factors in Eq. 2,1 amount to enforcing
convex combination, so there is only one degree of freedom
given our two element observation set. If
. The leading normalization
factors in Eq. 2,1 amount to enforcing
convex combination, so there is only one degree of freedom
given our two element observation set. If ![]() denotes
the weight of the first point, then the second has weight
denotes
the weight of the first point, then the second has weight
![]() . The induced mean is just
. The induced mean is just ![]() and the induced
variance
and the induced
variance
![]() . Our objective is to generate
a two element mixture which is class equivalent to an arbitrary one,
so two emphasis parameters
. Our objective is to generate
a two element mixture which is class equivalent to an arbitrary one,
so two emphasis parameters ![]() and
and ![]() are needed.
The two constant differences to be matched (from Eq. 7)
are denoted
are needed.
The two constant differences to be matched (from Eq. 7)
are denoted ![]() and
and ![]() .
That these are independent and unconstrained characteristics an
equivalence class follows from the observation that we may,
without loss of generality, set one of the target means to
zero. The constraints then become:
.
That these are independent and unconstrained characteristics an
equivalence class follows from the observation that we may,
without loss of generality, set one of the target means to
zero. The constraints then become:
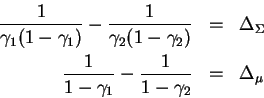
Choose
![]() . From our second constraint we have
. From our second constraint we have
![]() from which it
follows that
from which it
follows that
![]() only when they both are
only when they both are
![]() . But in this case
. But in this case
![]() , contradicting our
choice. So
, contradicting our
choice. So
![]() . Now when
. Now when ![]() ,
, ![]() , so here
, so here
![]() . Because
they are never equal, and their relationship is continuous,
this inequality must hold for any pair satisfying the
constraints. But it is easily verified that
. Because
they are never equal, and their relationship is continuous,
this inequality must hold for any pair satisfying the
constraints. But it is easily verified that
![]() whence this quantity is
negative. So no pair
whence this quantity is
negative. So no pair
![]() exists which
satisfies the constraints given say
exists which
satisfies the constraints given say
![]() and
and
![]() .
.
We remark that if instead, one is interested in matching the
a posteriori class behavior of a mixture at only the
given sample points, then the example's argument does not
apply. Indeed it may be verified that this less stringent
requirement can be satisfied. This is not entirely surprising
since given exactly ![]() sample points, one has three
free parameters, and must match only two. This is
interesting, and we conjecture that it is true more generally
for
sample points, one has three
free parameters, and must match only two. This is
interesting, and we conjecture that it is true more generally
for ![]() and
and ![]() - so long as
- so long as ![]() . In any
event, as a result of our arguments at the end of this
section, it cannot be true for arbitrarily large
. In any
event, as a result of our arguments at the end of this
section, it cannot be true for arbitrarily large ![]() . Since
we are interested in reparameterizing problems with
arbitrarily many samples, we will not consider the matter
further in this paper.
. Since
we are interested in reparameterizing problems with
arbitrarily many samples, we will not consider the matter
further in this paper.
The example above applies to dimension ![]() only, and a
particular set of sample points. Moreover, its analytical
approach does not generalize easily. We now show that in the
general case strict EM-style emphasis is not universal.
only, and a
particular set of sample points. Moreover, its analytical
approach does not generalize easily. We now show that in the
general case strict EM-style emphasis is not universal.
Without loss of generality we will assume
![]() - since
otherwise, the problem, and any solution thereto, can be
translated appropriately.
We may also assume the sample points are distinct.
Eq. 7 becomes:
- since
otherwise, the problem, and any solution thereto, can be
translated appropriately.
We may also assume the sample points are distinct.
Eq. 7 becomes:
where
![]() . Our focus is on the simple
rearrangement of Eq. 12:
. Our focus is on the simple
rearrangement of Eq. 12:
Independent of the
![]() we are free to
set
we are free to
set
![]() so that the
so that the
![]() have
arbitrary values. In particular, we will set them so that
have
arbitrary values. In particular, we will set them so that
![]() where
where ![]() is a constant.
is a constant.
Now focus on target mixtures such that
![]() has value
has value ![]() where
where
![]() .
Then
.
Then
![]() . So
independent of the choice of particular
. So
independent of the choice of particular
![]() , and
, and
![]() , each
, each
![]() , where
, where ![]() , will approach
, will approach ![]() .
There inverses therefore approach the diagonal matrix
.
There inverses therefore approach the diagonal matrix
![]() .
.
As
![]() , we adjust means as necessary
so as to maintain
, we adjust means as necessary
so as to maintain
![]() . Then
from Eq. 13 it is apparent that
. Then
from Eq. 13 it is apparent that
![]() is very nearly
a scaled up copy of the diagonal of
is very nearly
a scaled up copy of the diagonal of
![]() . Since the
off diagonal elements approach zero, it must eventually be the
case that
. Since the
off diagonal elements approach zero, it must eventually be the
case that
![]() . Also, since the sample
set is finite, it must eventually be that both are smaller
than say
. Also, since the sample
set is finite, it must eventually be that both are smaller
than say ![]() th of the smallest distance between sample
points. When this happens, the distance from
th of the smallest distance between sample
points. When this happens, the distance from
![]() to the
nearest sample will be at least
to the
nearest sample will be at least
![]() .
.
Now the covariance
![]() is a convex combination of
matrices of the form
is a convex combination of
matrices of the form
![]() -
and the diagonals are nonnegative.
The norm of
-
and the diagonals are nonnegative.
The norm of
![]() is at least equal to the norm of its
diagonal, but the diagonal is just the distance from the
sample point to
is at least equal to the norm of its
diagonal, but the diagonal is just the distance from the
sample point to
![]() . From this it follows that
. From this it follows that
![]() which presents a contradiction,
whence strict EM-style emphasis is not universal.
Our arguments above establish:
which presents a contradiction,
whence strict EM-style emphasis is not universal.
Our arguments above establish:
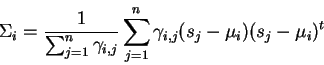
there exist target mixtures which may not be generated by emphasis.
We have seen that no number of sample points make strict EM-style emphasis universal. But given enough points, we can certainly identify a particular class equivalence-class, since all functions involved are analytic with a finite number of parameters. So given enough sample points, a reparameterization must be universal in order to match a target distribution at the sample points only. Now we are interested in reparameterizations which apply given an unlimited number of points. Therefore, unlike the modified emphasis reparameterization introduced in the previous section, strict EM-style reparameterization is simply not expressive enough to safely reparameterize a posteriori optimization problems.
The a posteriori degeneracy we clarify in section 2 for normal mixtures must be added to the list of interesting characteristics of Gaussians. We have not considered analogues of theorem 1 for other densities but remark that proposition 1 applies more generally. Beta densities, for example, have the property that their ratio is again of the same functional form so that a similar degeneracy arises. It seems likely that results similar in flavor to theorem 1 might be established for this and other related densities.
Another interesting area for future work relates to densities for
which there is essentially no degeneracy, i.e. for which the mixture
may be identified given its class behavior. A simple example is
provided by a mixture of two uniform univariate densities
![]() with support
with support
![]() and
and
![]() respectively. Here, a form of degeneracy
arises only when
respectively. Here, a form of degeneracy
arises only when
![]() . The mixture is still
identifiable but the mixing coefficients are not. This illustrates
the manner in which mixtures of densities of finite support might be
used to construct degeneracy-free mixtures. More complex and
interesting possibilities exist.
. The mixture is still
identifiable but the mixing coefficients are not. This illustrates
the manner in which mixtures of densities of finite support might be
used to construct degeneracy-free mixtures. More complex and
interesting possibilities exist.
The reparameterization of section 3 is of mathematical interest, and lends some credibility to approaches which attempt to maximize a posteriori probability by adjusting weights on the available samples - perhaps according to some error measure. An examination of reparameterization as a primary optimization technique, represents an interesting area for future work. We must however caution that while our proofs are constructive, we have not considered the matter of numerical sensitivity. Indeed, if one attempts to emulate a mixture using means far displaced from their natural locations, the mixing parameters become quite small. In these cases floating point underflow is a virtual certainty.
One should not interpret section 4 to say that strict EM-style emphasis will not work in practice for many problems. It merely exposes its theoretical limitations.
We thank Leonid Gurvits for several helpful discussions - and in particular for pointing out the simple factorization in proof of proposition 2, and simplifying our proof of proposition 3. We also thank Joe Kilian for several helpful discussions which contributed to our understanding of degeneracy and class equivalence.
This document was generated using the LaTeX2HTML translator Version 2K.1beta (1.47)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -image_type gif -nonext_page_in_navigation -noprevious_page_in_navigation -up_url ../main.html -up_title 'Publication homepage' -numbered_footnotes ert.tex
The translation was initiated by Peter N. Yianilos on 2002-06-30