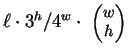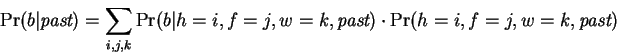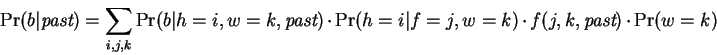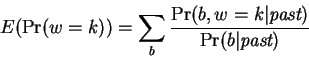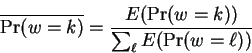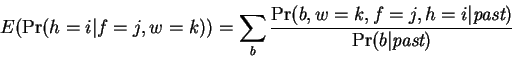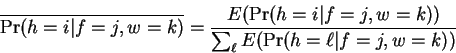Up: Publication homepage
Significantly Lower Entropy Estimates for Natural DNA Sequences
David Loewenstern*
NEC Research Institute, 4 Independence Way, Princeton, NJ
08540
Phone: 609-951-2798
Fax: 609-951-2483
Email: loewenst@paul.rutgers.edu
and
Peter N. Yianilos
NEC Research Institute, 4 Independence Way, Princeton, NJ
08540
and
Department of Computer Science
Princeton University, Princeton, New Jersey 08544
Email: pny@research.nj.nec.com
Submitted: November 10, 1996
Abstract:
If DNA were a random string over its alphabet 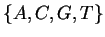 ,
an optimal code would assign
,
an optimal code would assign 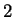 bits to each nucleotide. DNA
may be imagined to be a highly ordered, purposeful molecule, and
one might therefore reasonably expect statistical models of its
string representation to produce much lower entropy estimates.
Surprisingly this has not been the case for many natural DNA
sequences, including portions of the human genome. We
introduce a new statistical model (compression algorithm), the
strongest reported to date, for naturally occurring DNA
sequences. Conventional techniques code a nucleotide using
only slightly fewer bits (1.90) than one obtains by relying only on
the frequency statistics of individual nucleotides (1.95). Our
method in some cases increases this gap by more than
five-fold (1.66) and may lead to better performance in
microbiological pattern recognition applications.
bits to each nucleotide. DNA
may be imagined to be a highly ordered, purposeful molecule, and
one might therefore reasonably expect statistical models of its
string representation to produce much lower entropy estimates.
Surprisingly this has not been the case for many natural DNA
sequences, including portions of the human genome. We
introduce a new statistical model (compression algorithm), the
strongest reported to date, for naturally occurring DNA
sequences. Conventional techniques code a nucleotide using
only slightly fewer bits (1.90) than one obtains by relying only on
the frequency statistics of individual nucleotides (1.95). Our
method in some cases increases this gap by more than
five-fold (1.66) and may lead to better performance in
microbiological pattern recognition applications.
One of our main contributions, and the principle source of
these improvements, is the formal inclusion of inexact match
information in the model. The existence of matches at various
distances forms a panel of experts which are then combined
into a single prediction. The structure of this combination
is novel and its parameters are learned using Expectation
Maximization (EM).
Experiments are reported using a wide variety of DNA sequences
and compared whenever possible with earlier work. Four
reasonable notions for the string distance function used to
identify near matches, are implemented and experimentally
compared.
We also report lower entropy estimates for coding regions
extracted from a large collection of non-redundant human genes.
The conventional estimate is 1.92 bits. Our model produces
only slightly better results (1.91 bits) when considering
nucleotides, but achieves 1.84-1.87 bits when the prediction
problem is divided into two stages: i) predict the next amino
acid based on inexact polypeptide matches, and ii) predict the
particular codon. Our results suggest that matches at
the amino acid level play some role, but a small one, in determining
the statistical structure of non-redundant coding sequences.
Keywords:DNA, Information Theoretic Entropy, Expectation Maximization
(EM), Data Compression, Context Modeling, Time Series
Prediction.
The DNA molecule encodes information which by convention is
represented as a symbolic string over the alphabet 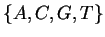 .
Assuming each character (nucleotide) is drawn uniformly at random from
the alphabet, and that all positions in the string are independent, we
know from elementary information theory
[Cover and Thomas, 1991,Bell et al., 1990] that an optimal code will devote
2 bits to representing each character. This is the maximum entropy
case. DNA may be imagined to be a highly ordered, purposeful molecule, and
one might therefore reasonably expect statistical models of its string
representation to produce much lower entropy estimates, and confirm
our intuition that it is far from random. Unfortunately this has not
been the case for many natural DNA sequences, including portions of
the human genome.
.
Assuming each character (nucleotide) is drawn uniformly at random from
the alphabet, and that all positions in the string are independent, we
know from elementary information theory
[Cover and Thomas, 1991,Bell et al., 1990] that an optimal code will devote
2 bits to representing each character. This is the maximum entropy
case. DNA may be imagined to be a highly ordered, purposeful molecule, and
one might therefore reasonably expect statistical models of its string
representation to produce much lower entropy estimates, and confirm
our intuition that it is far from random. Unfortunately this has not
been the case for many natural DNA sequences, including portions of
the human genome.
One example is the human retinoblastoma susceptibility gene
containing 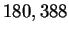 nucleotides, and referred to as HUMRETBLAS.
The alphabet members do not occur with equal frequency in this string,
and accounting for this yields an entropy estimate of roughly
nucleotides, and referred to as HUMRETBLAS.
The alphabet members do not occur with equal frequency in this string,
and accounting for this yields an entropy estimate of roughly 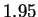 bits. This is perhaps not surprising since such single character
models are the weakest in our information theory arsenal.
A logical
next step taken by several investigators, focuses instead on higher
order entropy estimates arising from measurements of the frequencies
of longer sequences. For natural languages (e.g. English) this step
typically leads to significantly lower entropy estimates. But the best
resulting estimate for HUMRETBLAS is roughly
bits. This is perhaps not surprising since such single character
models are the weakest in our information theory arsenal.
A logical
next step taken by several investigators, focuses instead on higher
order entropy estimates arising from measurements of the frequencies
of longer sequences. For natural languages (e.g. English) this step
typically leads to significantly lower entropy estimates. But the best
resulting estimate for HUMRETBLAS is roughly 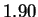 bits
[Mantegna et al., 1993], still not impressively different from our
bits
[Mantegna et al., 1993], still not impressively different from our  -bit
random starting point.
This may be something of a surprise, since such models reflect such
known DNA structure as
-bit
random starting point.
This may be something of a surprise, since such models reflect such
known DNA structure as 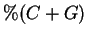 composition and CG suppression. But
these known effects have little impact on the entropy of DNA sequences
as a whole.
composition and CG suppression. But
these known effects have little impact on the entropy of DNA sequences
as a whole.
One may view DNA as a time series, and these higher order models
as predictors of the next nucleotide based on its immediate past.
With this interpretation the simple 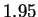 bit model relies on none of
the past. The
bit model relies on none of
the past. The 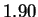 bit result is then even more surprising since it
implies that knowledge of the immediate past reduces the entropy
estimate by a mere
bit result is then even more surprising since it
implies that knowledge of the immediate past reduces the entropy
estimate by a mere 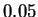 bits.1 Data compression techniques such as Lempel-Ziv (LZ)
coding [Ziv and Lempel, 1977] may be
viewed as entropy estimators, with LZ corresponding to a model that
predicts based on a historical context of variable length. It
``compresses'' HUMRETBLAS to
bits.1 Data compression techniques such as Lempel-Ziv (LZ)
coding [Ziv and Lempel, 1977] may be
viewed as entropy estimators, with LZ corresponding to a model that
predicts based on a historical context of variable length. It
``compresses'' HUMRETBLAS to 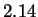 bits per
character2, which is actually worse than
the flat random model we started with. The authors' earlier efforts
implemented other advanced modeling techniques but failed to obtain
estimates below approximately
bits per
character2, which is actually worse than
the flat random model we started with. The authors' earlier efforts
implemented other advanced modeling techniques but failed to obtain
estimates below approximately 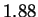 bits.
bits.
In this paper we describe a new statistical model, the strongest
we are aware of, for naturally occurring DNA sequences. The result is
lower entropy estimates for many sequences. Our
experiments include a wide variety of DNA, and in almost all cases our
model outperforms the best earlier reported results. For HUMRETBLAS, the
result is approximately 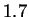 bits per character --
bits per character -- 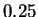 bits
improved from our
bits
improved from our 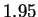 bit starting level. The standard higher
order estimate of
bit starting level. The standard higher
order estimate of 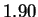 bits is only
bits is only 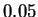 bits lower, so in this
sense our result represents a five-fold improvement. In every case
our model outperforms the most common techniques. These results are
significant because of our model's consistent and frequently substantial advantage
over earlier methods.
bits lower, so in this
sense our result represents a five-fold improvement. In every case
our model outperforms the most common techniques. These results are
significant because of our model's consistent and frequently substantial advantage
over earlier methods.
So far we have described the quest for lower entropy estimates as
a rather pure game, i.e. to predict better an
unknown nucleotide based on the rest of the sequence. There are both
conceptual and practical reasons to believe that this is an
interesting pursuit and that our experimental results are of some
importance. Conceptually, the pursuit of better models for data
within some domain corresponds rather directly to the discovery of
structure in that domain. That is, we model so that we can better
understand. Practically, statistical modeling of DNA has proven to be
somewhat effective in several problem areas, including the automatic
identification of coding regions
[Lauc et al., 1992,Cosmi et al., 1990,Cardon and Stormo, 1992,Farach et al., 1995,Krogh et al., 1994], and in
classifying unknown sequences into one of a discrete number of
classes. The success of such methods ultimately rests on the strength
of the models they employ.
In section 2 we discuss the interpretation of
entropy estimates obtained by methods such as ours, and by other
approaches such as data compressors. The definition of entropy in the
context of DNA nucleotide prediction is made more precise, and
we discuss entropy estimates for coding regions.
A detailed exposition of our model is presented in section 3,
but we first introduce and motivate it here in general terms.
Conventional
fixed-context models focus on a trailing context, i.e. the immediately
preceding nucleotides. Longer
contexts reach farther into the past, and might reasonably be expected
to result in stronger models. However as context length increases, it
becomes increasingly unlikely that a given context has ever been
seen. This problem has led to the development of variable length
context language models [Bell et al., 1990], which
use long contexts when enough earlier observations exists, and
otherwise use shorter ones. Since as earlier noted, the short-term
behavior of many natural DNA sequences is so nearly random, these more
advanced variable length schemes do not push farther into the past,
except in the unusual event of a long exact repeat.
The basic idea behind our model is to push farther into the past by
relaxing the exact-match requirement for contexts.
Our formalization
of this idea in section 3 is one of the main
contributions of this paper.
The metric for determining quality of match is primarily a
simple Hamming distance, but in the interests of exploring the use of
additional biological knowledge, three other metrics
were evaluated in section 6.
We also describe a two-stage model for coding regions in which an
amino acid is first
predicted based on earlier amino acids, followed by the prediction
of a particular codon.
Section 6 concludes with a discussion that suggests why
the high entropy levels observed for coding regions may not be
so surprising after all.
Entropy Estimation and Data Compression
The term entropy estimate can be somewhat vague. This section
continues our introduction of the term by clarifying its various senses as they
relate to DNA, and its relationship to data compression and
prediction. We include the section in part to answer some of the most
frequently asked basic questions about this work. Our discussion will
first focus on the sense of entropy that corresponds to a
stochastic process. Later, we describe another equivalent sense more suited to
sequences of finite extent. The entropy rate of a stochastic
process 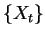 is defined as:
is defined as:
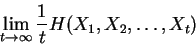 |
(1) |
where this limit need not in general exist, and 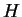 denotes
the information theoretic entropy function (see [Cover and Thomas, 1991].)
Given full knowledge of the process, and the limit's existence, the
entropy rate is a well-defined attribute of the process. But we know
very little of the process underlying the generation of natural DNA,
and can merely observe the outcome, i.e. the nucleotide sequence.
Given a predictive model
denotes
the information theoretic entropy function (see [Cover and Thomas, 1991].)
Given full knowledge of the process, and the limit's existence, the
entropy rate is a well-defined attribute of the process. But we know
very little of the process underlying the generation of natural DNA,
and can merely observe the outcome, i.e. the nucleotide sequence.
Given a predictive model 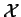 , and a long DNA sequence
, and a long DNA sequence 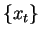 ,
we are therefore content to consider:
,
we are therefore content to consider:
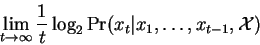 |
(2) |
This may be thought of as the average bits per symbol
required to code increasingly long observation sequences. If our
model matches Nature perfectly, Nature's process is in some sense
well-behaved3,
and our sequence is of infinite length, then this limit matches the
entropy rate. Of course: i) our model does not match Nature, ii)
there is no reason to believe Nature is in the required sense
well-behaved, and iii) we can observe only finite DNA sequences. It
is in this sense that one is computing an entropy estimate when
an imperfect model is applied to a finite empirically observed
sequence.
Given a data compression program, Equation 2 may
therefore be approximated by dividing the number of bits output by
the number of symbols (nucleotides) input. We will refer to
computations like this as purely compressive entropy estimates.
Most existing compression algorithms, when applied to natural data, do
in fact frequently approach a limit in bits/character -- their
estimate of the source's entropy. Unless the sequence being
compressed is very long, the purely compressive estimate then
overstates the actual entropy. One might then focus only on the
code-lengths near the end of the sequence. The risk however is then
that the end might just happen to be more predictable and not reflect
the overall entropy. For example, the end might, in the case of DNA,
contain many long exact repeats of earlier segments. This suggests
our second approach, that of cross-validation entropy estimates.
Here the sequence is first partitioned into 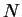 equal size segments.
The entropy of each segment is then computed by coding it having first
trained the model using the remaining segments. The reported entropy
estimate is the average of these
equal size segments.
The entropy of each segment is then computed by coding it having first
trained the model using the remaining segments. The reported entropy
estimate is the average of these 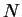 estimates. One can imagine that
each of these estimates moves one segment to the end of the sequence,
codes it, and averages code-lengths for the final segment only. As
estimates. One can imagine that
each of these estimates moves one segment to the end of the sequence,
codes it, and averages code-lengths for the final segment only. As
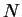 increases, the individual cross-validation estimates may be
plotted to visualize the instantaneous entropy rate as a function of
position in the sequence. Several of these plots are presented in
section 5.
increases, the individual cross-validation estimates may be
plotted to visualize the instantaneous entropy rate as a function of
position in the sequence. Several of these plots are presented in
section 5.
In what follows, we will switch without harm between a compressive
viewpoint, that of stochastic prediction in which the objective is to
predict the next nucleotide, and generative stochastic modeling in
which one imagines the data to emanate from a particular process.
This is possible because a generative process gives rise to a
prediction, and a prediction can be converted to a code via arithmetic
coding. Starting from a data compressor, we can think of the bits
output for a single input symbol, as 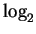 of the probability that
a corresponding predictor will predict, or generator will generate
that symbol4.
of the probability that
a corresponding predictor will predict, or generator will generate
that symbol4.
The models discussed so far in this paper introduce only one kind of domain
knowledge: that natural DNA sequences include more near
repetitions than one expects at random. Part of the
reason that so little effort has been devoted to more advanced models
that incorporate complex domain knowledge, is that models of the
ignorant variety do a very good job of modeling other natural
sequences. For example, Shannon's work estimated the entropy of
English text to be roughly 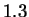 bits per character (see discussion in
[Bell et al., 1990]). Random text over a 27 letter alphabet (A-Z
and space) corresponds to
bits per character (see discussion in
[Bell et al., 1990]). Random text over a 27 letter alphabet (A-Z
and space) corresponds to 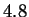 bits. Today's statistical models,
with no specific knowledge of English syntax or semantics, can achieve
roughly
bits. Today's statistical models,
with no specific knowledge of English syntax or semantics, can achieve
roughly 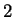 bits.
bits.
Returning to the question that opened our discussion, we submit that
the essential cause of our surprise is that simple statistical models,
which perform so well in other cases, fail to discover significant
structure in DNA. Our work demonstrates that DNA is more predictable than
had previously been established, but falls far short of the
compression levels easily achieved for natural language.
This suggests that local structure parallel to ``words'' and
``phrases'' is largely missing in DNA, even when the exact match
requirement is relaxed.
As to ``what entropy level we expect and why'', we believe that the
question ultimately comes down to one of quantifying the magnitude of
the functional degeneracy of polypeptides. That is, how many
different sequences are essentially equivalent functionally? If this
degeneracy turns out to be large, then DNA is to its function, as an
acoustic waveform is to human speech. That is, small local
distortions do little to alter the overall message.
This is discussed further in Section 6.
Algorithms
In this section we further motivate our model and then describe it in
formal terms.
That natural DNA includes near repeats is well known, and in
[Herzel, 1988] the statistics of their occurrence are discussed. We
measure nearness using ordinary Hamming distance,
i.e. the number of positions at which two equal length
strings disagree. Given a target string of length 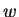 , it is then
natural to wonder how many
, it is then
natural to wonder how many 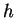 -distant matches exist in a string of
length
-distant matches exist in a string of
length 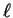 . As remarked earlier, DNA seems very nearly random over
short distances. Assuming uniform randomness it is easily shown that
we expect to see
. As remarked earlier, DNA seems very nearly random over
short distances. Assuming uniform randomness it is easily shown that
we expect to see
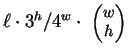
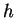 -distant
matches. Natural DNA sequences depart markedly from this behavior,
providing one part of the motivation for our model.
For example
(table 1), using HUMRETBLAS, which consists of
-distant
matches. Natural DNA sequences depart markedly from this behavior,
providing one part of the motivation for our model.
For example
(table 1), using HUMRETBLAS, which consists of
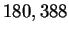 nucleotides, and a randomly chosen substring of length
nucleotides, and a randomly chosen substring of length
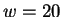 from the first
from the first 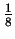 of the sequence, one expects
of the sequence, one expects
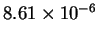 Hamming
distance
Hamming
distance 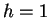 matches in the last
matches in the last 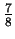 of the sequence under the random
model. We actually see
of the sequence under the random
model. We actually see 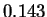 where again, this is an average over
all
length
where again, this is an average over
all
length 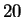 targets in the last
targets in the last 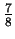 of HUMRETBLAS. When such matches exist, examination of the following
nucleotide yields a prediction that is correct
of HUMRETBLAS. When such matches exist, examination of the following
nucleotide yields a prediction that is correct 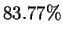 of the time.
That these matches, when present, lead to good predictions is a second
motivating factor. Unfortunately such Hamming distance
of the time.
That these matches, when present, lead to good predictions is a second
motivating factor. Unfortunately such Hamming distance 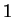 matches
occur for only
matches
occur for only 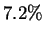 of the positions in HUMRETBLAS, so alone,
this effect is unlikely to lead to much better predictions on average.
But if one again refers to table 1, roughly
of the positions in HUMRETBLAS, so alone,
this effect is unlikely to lead to much better predictions on average.
But if one again refers to table 1, roughly 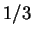 of
the positions have an earlier match at distance
of
the positions have an earlier match at distance 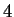 - and at even
this distance, predictions based on past matches are correct
- and at even
this distance, predictions based on past matches are correct 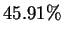 of the time. The potential effectiveness of predictions based on
matches at all distances is our final motivating factor. The
objective, then, is to combine these weak information sources to form a
prediction. Also, a version of table 1 may be made
for multiple windows. Our model combines all of this information and
makes a single prediction.
The use of near matches for
prediction is certainly consistent with an evolutionary view in which
Nature builds a genome in part by borrowing mutated forms of her
earlier work.
of the time. The potential effectiveness of predictions based on
matches at all distances is our final motivating factor. The
objective, then, is to combine these weak information sources to form a
prediction. Also, a version of table 1 may be made
for multiple windows. Our model combines all of this information and
makes a single prediction.
The use of near matches for
prediction is certainly consistent with an evolutionary view in which
Nature builds a genome in part by borrowing mutated forms of her
earlier work.
One may view each row of table 1
(really each Hamming distance) as corresponding to a predictive
expert,
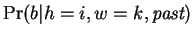 . The prediction of the Hamming
distance
. The prediction of the Hamming
distance 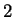 expert,
expert,
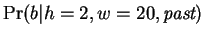 is formed
by examining all past matches exactly this distance from our trailing
context window, and capturing the distribution of following
nucleotides by maintaining a simple table of counters. The simplest
way to combine these experts is by a fixed set of weights that sum to
one.
is formed
by examining all past matches exactly this distance from our trailing
context window, and capturing the distribution of following
nucleotides by maintaining a simple table of counters. The simplest
way to combine these experts is by a fixed set of weights that sum to
one.
But suppose that while trying to predict a particular nucleotide 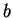 using
using 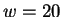 , our past experience includes no Hamming distance
, our past experience includes no Hamming distance
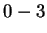 matches, i.e. the closest past window is distance
matches, i.e. the closest past window is distance 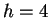 . This
information is known before we see the to-be-predicted
nucleotide and may therefore influence the prediction. In particular
it makes no sense to give any weight to the opinions of the first
three experts -- in fact their opinion is not even well-defined in
this case. Only the
. This
information is known before we see the to-be-predicted
nucleotide and may therefore influence the prediction. In particular
it makes no sense to give any weight to the opinions of the first
three experts -- in fact their opinion is not even well-defined in
this case. Only the 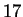 experts corresponding to Hamming distances
experts corresponding to Hamming distances
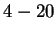 are relevant. We're then interested in properly weighting them
conditioned on the assumption that the closest match we've seen lies
at distance
are relevant. We're then interested in properly weighting them
conditioned on the assumption that the closest match we've seen lies
at distance 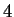 . In what follows we will refer to this value as
first Hamming,
. In what follows we will refer to this value as
first Hamming, 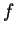 . Finally, since we don't know a priori how
window size will influence the prediction, our model is formed at the
uppermost level by a mixture of models, each considering a fixed
window size from some fixed prior set.
. Finally, since we don't know a priori how
window size will influence the prediction, our model is formed at the
uppermost level by a mixture of models, each considering a fixed
window size from some fixed prior set.
We denote by 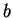 the discrete random variable representing the
nucleotide (base-pair) to be predicted. Its four values are
the discrete random variable representing the
nucleotide (base-pair) to be predicted. Its four values are
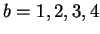 and correspond to
and correspond to 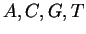 . By
. By 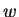 we denote the
positive integer random variable corresponding to the length of our
trailing context window. The set of values it may assume is parameter
of the model, defined by specifying non-zero prior probabilities for
only a finite subset of the positive integers. For example, allowing
we denote the
positive integer random variable corresponding to the length of our
trailing context window. The set of values it may assume is parameter
of the model, defined by specifying non-zero prior probabilities for
only a finite subset of the positive integers. For example, allowing
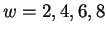 considers context windows of these four lengths. Next,
considers context windows of these four lengths. Next,
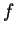 denotes the first Hamming distance to be considered. It may
assume values
denotes the first Hamming distance to be considered. It may
assume values 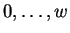 . By
. By 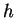 we denote the index of each
Hamming distance expert. So
we denote the index of each
Hamming distance expert. So 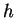 lies in the range
lies in the range 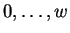 .
Finally, we use
.
Finally, we use
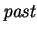 to represent our modeling past, i.e. the DNA
that we have either already predicted, or have set aside as reference
information.
to represent our modeling past, i.e. the DNA
that we have either already predicted, or have set aside as reference
information.
Given a fixed window size 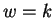 , and distance
, and distance 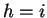 , there is a
natural prediction
, there is a
natural prediction
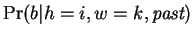 formed by locating all
distance
formed by locating all
distance 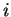 matches in the past to the trailing context of length
matches in the past to the trailing context of length
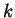 , and then using the distribution of nucleotides that follow them.
This is a single expert as described above. This prediction is
independent of
, and then using the distribution of nucleotides that follow them.
This is a single expert as described above. This prediction is
independent of 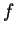 so
so
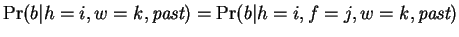 . Our prediction
. Our prediction
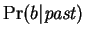 arises from
the joint probability
arises from
the joint probability
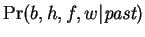 by summing over the
hidden variables
by summing over the
hidden variables 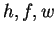 as follows:
as follows:
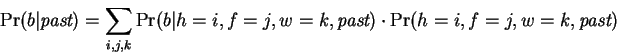 |
(3) |
The final term is then expressed as a product of
conditionals:
In this expression
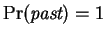 and
and
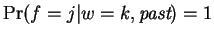 for
for 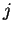 equal to the distance of the closest match to our
trailing context window of length
equal to the distance of the closest match to our
trailing context window of length 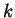 , in the
, in the
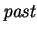 . At all other
values
. At all other
values
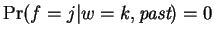 . That is,
. That is,
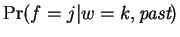 is a boolean function
is a boolean function
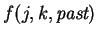 .
Next, we assume
.
Next, we assume 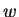 is independent of the past in our model, so
is independent of the past in our model, so
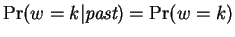 and consists of a vector of fixed mixing
coefficients that select a window size. Introducing a dependency
here may improve the model and represents an interesting area for
future work. Finally, in our model
and consists of a vector of fixed mixing
coefficients that select a window size. Introducing a dependency
here may improve the model and represents an interesting area for
future work. Finally, in our model
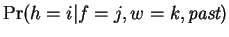 is also
independent of the past and consists of a fixed vector of
is also
independent of the past and consists of a fixed vector of 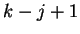 mixing coefficients that select a Hamming distance given the earlier
choice of a window size
mixing coefficients that select a Hamming distance given the earlier
choice of a window size 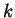 , and observation that the nearest past
match is at distance
, and observation that the nearest past
match is at distance 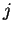 . We then have:
. We then have:
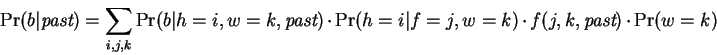 |
(5) |
The first term in the summation is recognized as a single
expert, the second selects an expert based on 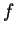 and
and 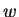 , the third
deterministically selects a single
, the third
deterministically selects a single 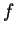 value, which receives
probability
value, which receives
probability 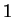 , and the final term selects a window size. The first
and third terms are determined entirely from the current context and
the past; the second and fourth terms are selection parameters that
must be tuned during a learning process.
, and the final term selects a window size. The first
and third terms are determined entirely from the current context and
the past; the second and fourth terms are selection parameters that
must be tuned during a learning process.
The model may also be viewed generatively (reading from left to right)
as depicted in figure 1. In this example a window
size 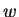 is first chosen from the set
is first chosen from the set
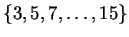 . The
probability of each choice is shown beside it. Notice that they, and
all choices at each node in the diagram, sum to unity. In the figure,
. The
probability of each choice is shown beside it. Notice that they, and
all choices at each node in the diagram, sum to unity. In the figure, 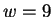 is
chosen and the next choice is deterministic. Here we've assumed that
the closest match to our trailing context of length
is
chosen and the next choice is deterministic. Here we've assumed that
the closest match to our trailing context of length 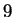 is distance
is distance
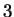 away. Now given
away. Now given 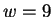 and
and 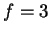 we choose
we choose
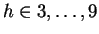 with
the probabilities shown. Here we've assumed that
with
the probabilities shown. Here we've assumed that 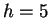 is chosen.
Finally, given all the earlier choices, we generate a nucleotide
is chosen.
Finally, given all the earlier choices, we generate a nucleotide 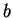 according to probabilities shown.
according to probabilities shown.
Figure 1:
An illustration of the generative branching process
that corresponds to the predictive model of this paper.
 |
We refer again to figure 1 to clarify the model's
parameter structure. The probabilities associated with the choice of
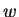 are parameters, as are those associated with the choice of
are parameters, as are those associated with the choice of 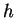 for
each
for
each 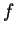 and
and 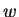 . But recall that the probabilities on each
. But recall that the probabilities on each 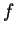 arc
in the graph are computed and are not therefore parameters. Similarly
the probabilities associated with
arc
in the graph are computed and are not therefore parameters. Similarly
the probabilities associated with 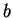 are not parameters. They too
are computed and represent the opinion of a single expert as
described earlier. Thus for the figure shown there are
are not parameters. They too
are computed and represent the opinion of a single expert as
described earlier. Thus for the figure shown there are 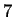 parameters
for
parameters
for 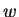 , and
, and
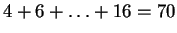 associated with
associated with 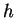 , for a total of
, for a total of
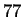 . Other parameters include our selection of window sizes to
consider, and several explained below having to do with the learning
algorithm.
. Other parameters include our selection of window sizes to
consider, and several explained below having to do with the learning
algorithm.
The learning task before us is to estimate these parameters by
examining the training set. Our algorithm is an application of the
Baum-Welch algorithm for Hidden Markov Models
[Baum and Eagon, 1967,Baum et al., 1970,Baum, 1972,Poritz, 1988], and may also be viewed as an
instance of Expectation Maximization (EM), a later rediscovery
[Dempster et al., 1977,Redner and Walker, 1984] of essentially the same algorithm and underlying
information theoretic inequality.
The Baum-Welch algorithm is an optimization technique which locally
maximizes the probability of generating the training set from the
model by adjusting parameters. A global optimization method would be
expected to yield better results in general. In the general case,
however, the problem of globally optimizing directed acyclic
graph-based models is known to be NP-complete (see [Yianilos, 1997, p. 32]). Our model fits within this class but we have not
considered the complexity of its optimization. It is known, however,
to exhibit multiple local optima.5
In the case of our model, the parameters are
the probability associated with 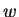 ,
, 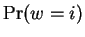 , and the probability
associated with
, and the probability
associated with 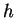 ,
,
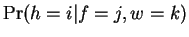 .
Before learning begins, these parameters are
initialized in our implementation to the flat (uniform) distribution.
Examples from the training set are now presented repeatedly, and these
parameters are reestimated upon each presentation -- climbing away
from their starting values towards some set of values that locally
maximize the log likelihood of the training set.
.
Before learning begins, these parameters are
initialized in our implementation to the flat (uniform) distribution.
Examples from the training set are now presented repeatedly, and these
parameters are reestimated upon each presentation -- climbing away
from their starting values towards some set of values that locally
maximize the log likelihood of the training set.
The training set consists of a series of prediction problems: predict
a given nucleotide 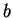 using its trailing context and some past
reference DNA. For the experiments of this paper, we select positions
to be predicted at random from the training DNA. The rest of the
sequence then serves as reference when searching for near-matches.
Because of the simple tree-like branching structure of our model, the
reestimation formulae are particularly simple and natural.
Accumulated expectations are first computed by:
using its trailing context and some past
reference DNA. For the experiments of this paper, we select positions
to be predicted at random from the training DNA. The rest of the
sequence then serves as reference when searching for near-matches.
Because of the simple tree-like branching structure of our model, the
reestimation formulae are particularly simple and natural.
Accumulated expectations are first computed by:
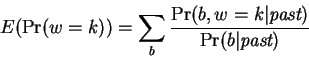 |
(6) |
where the probabilities are assumed to be conditioned on the
model's current parameter set, and the summation is over our randomly
chosen positions to be predicted. The reestimated window selection
probabilities are then:
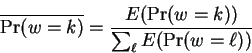 |
(7) |
Expectations for 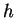 are accumulated according to:
are accumulated according to:
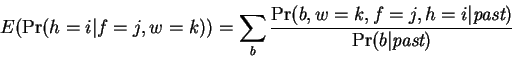 |
(8) |
The reestimated conditional Hamming distance selection
probabilities are then:
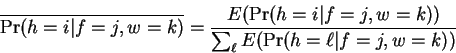 |
(9) |
This new parameter set
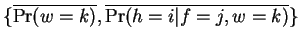 must increase
the likelihood of the training set under the model. Performing the
steps above once corresponds to one EM iteration. Each
iteration will
continue to improve the model unless a local maximum is reached. In
section 5 we will study the effect of these
iterations on the performance of our model, and also examine the
model's sensitivity to other parameters.
must increase
the likelihood of the training set under the model. Performing the
steps above once corresponds to one EM iteration. Each
iteration will
continue to improve the model unless a local maximum is reached. In
section 5 we will study the effect of these
iterations on the performance of our model, and also examine the
model's sensitivity to other parameters.
At the conclusion of each reestimation step above, the reestimated vector is
normalized to sum to unity. This operation is also performed when an
expert converts counts derived from earlier matches into a
stochastic prediction for the next nucleotide. In both places it is
possible for one or even all vector locations to be zero. The result
is then one or more zero probabilities after normalization. If the
entire vector is zero, the normalization operation is of course no
longer even well-defined. To ensure that our system deals only with
finite code-lengths, and to handle the all-zero case simply, we, as a
practical expedient, add a small constant,
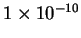 , to each
vector position before normalization. We stress that this is not done
for the same reason that one might use Laplace's rule (add one to
event counts) to flatten the prediction of a simple frequency-based
model. Such techniques are basically a remedy for data sparseness.
We require no such flattening since our model is itself a mixture of
many experts, including some for which plenty of data is
available. Experiments confirm our intuition that additional
Laplace-style flattening is in fact harmful.
, to each
vector position before normalization. We stress that this is not done
for the same reason that one might use Laplace's rule (add one to
event counts) to flatten the prediction of a simple frequency-based
model. Such techniques are basically a remedy for data sparseness.
We require no such flattening since our model is itself a mixture of
many experts, including some for which plenty of data is
available. Experiments confirm our intuition that additional
Laplace-style flattening is in fact harmful.
We conclude by sketching the operation of a fully on-line model.
Rather than performing EM iterations on a training set, expectations
are accumulated as each new nucleotide is predicted. The model is
then updated via the normalization (maximization) steps above before
the next character is processed. To deal with data sparsity early on,
normalization operations employ more aggressive flattening than above,
but the constant employed decays over time to some very small value
such as that above. The mathematical behavior of this algorithm is
not as well understood as that of conventional offline training, and we
will therefore study it independently in our future work.
Experimental Data
The DNA sequences were chosen to pass the following criteria:
sufficient length to support this type of entropy estimation method,
inclusion of a wide variety of species and sequence types to evaluate
the generality of the method, and inclusion of sequences used to
benchmark other published methods. All sequences are from GenBank
Release No. 92.0 of 18 December 1995. They are: thirteen mammalian
genes (GenBank loci HSMHCAPG, HUMGHCSA, HUMHBB, HUMHDABCD,
HUMHPRTB, HUMMMDBC, HUMNEUROF, HUMRETBLAS, HUMTCRADC, HUMVITDBP,
MMBGCXD, MUSTCRA, RATCRYG), a long mammalian intron (HUMDYSTROP), a C. elegans cosmid (CEC07A9), seven
prokaryote genes (BSGENR, ECO110K, ECOHU47, ECOUW82, ECOUW85,
ECOUW87, ECOUW89), a yeast chromosome (SCCHRIII), a plant
chloroplast genome (CHNTXX), two mitochondrial genomes (MPOMTCG, PANMTPACGA), five eukaryotic viral genomes (ASFV55KB,
EBV, HE1CG, HEHCMVCG, VACCG), and three bacteriophage genomes (LAMCG, MLCGA, T7CG).
There has been considerable discussion in the literature of the
statistical differences between coding and noncoding regions. To
support our study of this issue we assembled several long strands
consisting of purely coding or noncoding DNA. These sequences were
formed by concatenating coding or non-coding regions from one or more
of the above DNA sequences. We consider a region to be coding if
either the sense or anti-sense strand is translated; otherwise it is
non-coding.
To gather a larger body of coding regions, we obtained a data set
of 490 complete human genes. This data set was screened to remove any
partial genes, pseudogenes, mutants, copies, or variants of the same
gene [Noordewier, 1996]. The resulting sequence contains 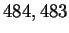 bases and is referred to as our non-redundant data set.
bases and is referred to as our non-redundant data set.
Experimental Results
Our model's performance on the sequences described in
section 4 is summarized in table 2. In
some cases our results may be compared directly with estimates from
[Grumbach and Tahi, 1994], which are included in the table. Our values for
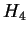 (the 4-symbol entropy) may be compared with the
redundancy estimates of [Mantegna et al., 1993] and are in agreement. We
have grouped our results by general type (i.e. mammalian, prokaryote,
etc.).
(the 4-symbol entropy) may be compared with the
redundancy estimates of [Mantegna et al., 1993] and are in agreement. We
have grouped our results by general type (i.e. mammalian, prokaryote,
etc.).
The 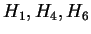 columns contain conventional multigram entropy
estimates. The CDNA column reports our model's cross-validation
entropy estimates. Compressive estimates from the BIOCOMPRESS-2
program of [Grumbach and Tahi, 1994] are contained in the following column.
Our model's compressive estimates are given in the table's final
column, CDNA-compress.
The compressive estimates are generated by partitioning the sequence
into 20 equal segments:
columns contain conventional multigram entropy
estimates. The CDNA column reports our model's cross-validation
entropy estimates. Compressive estimates from the BIOCOMPRESS-2
program of [Grumbach and Tahi, 1994] are contained in the following column.
Our model's compressive estimates are given in the table's final
column, CDNA-compress.
The compressive estimates are generated by partitioning the sequence
into 20 equal segments:
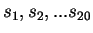 . The entropy estimate
for
. The entropy estimate
for 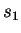 ,
, 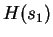 is
is 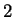 bits/nucleotide.
bits/nucleotide. 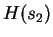 is calculated using
CDNA training on
is calculated using
CDNA training on 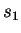 and testing on
and testing on 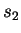 .
. 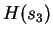 is
calculated from CDNA trained on
is
calculated from CDNA trained on 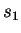 and
and 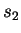 , tested on
, tested on
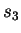 , and so forth. The overall estimate for CDNA-compress is
, and so forth. The overall estimate for CDNA-compress is
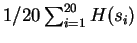 .
.
The reported CDNA and CDNA-compress results depend on
several model parameters. Their values and a sensitivity analysis are
given later in this section.
In the mammalian group, ``14
Sequences'', and the similarly named lines elsewhere in the table,
represent the average of the
entropy estimates for all relevant individual sequences,
weighted by sequence length.
The conventional multigram entropy results are in general not too informative.
It is interesting however to note the variation among sequences in even
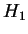 , the distribution of individual nucleotides. Only two of these estimates
are below
, the distribution of individual nucleotides. Only two of these estimates
are below 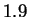 bits:
bits: 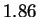 bits for both HUMGHCSA and PANMTPACGA. In
the first case CDNA reports
bits for both HUMGHCSA and PANMTPACGA. In
the first case CDNA reports 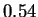 bits. This is a very repetitive sequence
and CDNA is able to exploit this to produce the lowest entropy estimate
we observed for any sequence. In this case of PANMTPACGA, nearly all of the
redundancy is explained by the unigraph statistics
bits. This is a very repetitive sequence
and CDNA is able to exploit this to produce the lowest entropy estimate
we observed for any sequence. In this case of PANMTPACGA, nearly all of the
redundancy is explained by the unigraph statistics 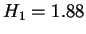 .
The observed relationship between
.
The observed relationship between 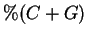 and gene density [Dujon et al., 1994] in yeast is reflected in the discrepancy
in
and gene density [Dujon et al., 1994] in yeast is reflected in the discrepancy
in 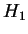 between the coding and non-coding region of Yeast chromosome
III.
between the coding and non-coding region of Yeast chromosome
III.
observe that the 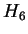 estimate is rarely better than
estimate is rarely better than 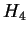 , and in some cases
is markedly worse (a consequence of limited sequence length).
, and in some cases
is markedly worse (a consequence of limited sequence length).
As a point of comparison, entropy rate was also estimated simply by
compressing the ASCII representation of the sequence using the UNIX compress utility and dividing the length of the compressed
sequence by the length of the uncompressed sequence. Because of
its limited dictionary size, the utility cannot be expected to
converge to a good entropy estimate for long, complex sequences. For
shorter sequences (roughly, sequences not greatly longer than 32,000
nucleotides), this limitation should have no impact.
Notice that in all cases, the UNIX compress utility performs
worse than no model at all (uniformly random prediction).
Figure 2:
Comparison of results.
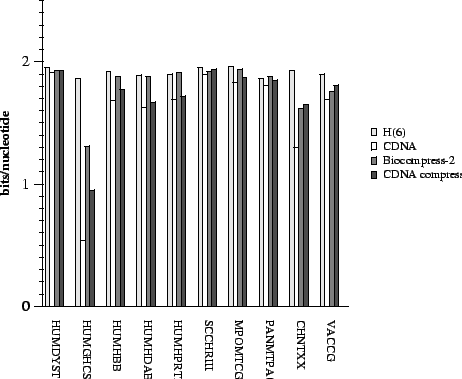 |
To make comparisons among entropy estimation methods clearer,
figure 2 summarizes the results from
table 2 for CDNA, 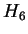 , BIOCOMPRESS-2, and
CDNA-compress.
In all cases CDNA outperforms conventional entropy estimates,
and in almost all cases by a substantial margin. In many cases the
compressive estimates from CDNA
(i.e., CDNA-compress) are lower than those of
BIOCOMPRESS-2.
In several they are comparable, and
in only one case (VACCG) does BIOCOMPRESS-2 outperform CDNA-compress by as much as 0.05 bits.
It is possible that
even this case
is due to the offline nature of the current CDNA program which as
mentioned above forces us to compute compressive estimates by dividing
the sequence into large segments.
Finally, we remark that while the
table contains results for HUMRETBLAS, this sequence was used in
our parameter sensitivity study below.
, BIOCOMPRESS-2, and
CDNA-compress.
In all cases CDNA outperforms conventional entropy estimates,
and in almost all cases by a substantial margin. In many cases the
compressive estimates from CDNA
(i.e., CDNA-compress) are lower than those of
BIOCOMPRESS-2.
In several they are comparable, and
in only one case (VACCG) does BIOCOMPRESS-2 outperform CDNA-compress by as much as 0.05 bits.
It is possible that
even this case
is due to the offline nature of the current CDNA program which as
mentioned above forces us to compute compressive estimates by dividing
the sequence into large segments.
Finally, we remark that while the
table contains results for HUMRETBLAS, this sequence was used in
our parameter sensitivity study below.
The CDNA program's behavior is parameterized by several values:
- The number of EM iterations to perform when learning
the model's parameters based on the training set.
- The set of allowed window sizes (trailing contexts).
- The size of the training sample.
- The size of the test sample.
- The number of cross-validation segments.
- The random seed that controls all sampling.
- The distance measure to use.
The distance measure is discussed later in
section 6 and for all other experiments is fixed
as described earlier. We used 3-way cross-validation to assess
parameter sensitivity (see discussion below), and 8-way
cross-validation for all experiments. Our test samples were of size
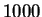 per cross-validation segment for a total of
per cross-validation segment for a total of 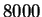 positions.
To assess the variation due to all sampling, we performed
positions.
To assess the variation due to all sampling, we performed 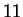 different cross-validation estimates using different random seeds.
The mean entropy estimate for HUMRETBLAS was
different cross-validation estimates using different random seeds.
The mean entropy estimate for HUMRETBLAS was 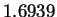 bits with
a standard deviation of
bits with
a standard deviation of 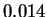 bits. Larger samples would result in
smaller variance at the expense of computer time.
bits. Larger samples would result in
smaller variance at the expense of computer time.
Figure 3 shows the effect of EM iterations on the
entropy estimate for both training and test sets. This figure and the
two that follow employ HUMRETBLAS. Based on this analysis, we
chose 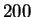 EM iterations for our experiments. Notice that there is
little overtraining. Both train and test performance are
essentially constant after
EM iterations for our experiments. Notice that there is
little overtraining. Both train and test performance are
essentially constant after 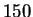 iterations, and their gap is small.
iterations, and their gap is small.
Figure 3:
The effect of varying the number of EM learning
iterations on performance for HUMRETBLAS.
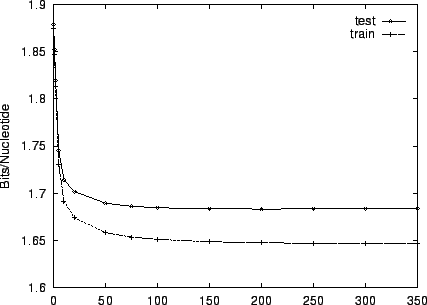 |
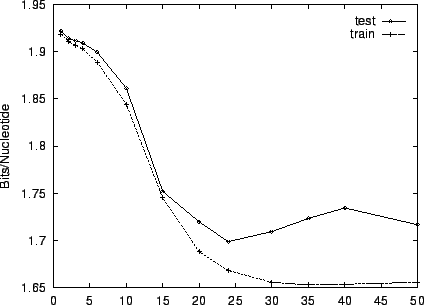
Figure 4 shows the effect of a single window size on
performance. Beyond 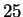 ,
overtraining is evident. This is to be
expected since the number of parameters grows quadratically with window
size. For our experiments we selected a mixture of windows of size
,
overtraining is evident. This is to be
expected since the number of parameters grows quadratically with window
size. For our experiments we selected a mixture of windows of size
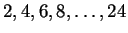 . Odd values were excluded only to reduce memory
requirements for the model. Additional experiments indicated that
while mixtures of different window sizes did in general help, the
benefit was somewhat small. We did not study this for all
sequences and therefore employed a mixture to ensure that the model is
as general as possible (in theory the mixture can only help).
. Odd values were excluded only to reduce memory
requirements for the model. Additional experiments indicated that
while mixtures of different window sizes did in general help, the
benefit was somewhat small. We did not study this for all
sequences and therefore employed a mixture to ensure that the model is
as general as possible (in theory the mixture can only help).
Figure 4:
The effect of varying the trailing context size
(window) on performance for HUMRETBLAS.
 |
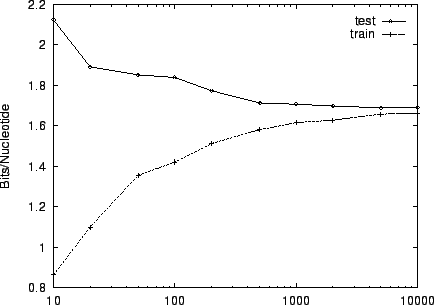
Finally, figure 5 shows the sensitivity of
performance on training set size. We used a training set of size
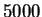 for our experiments because beyond that point, little
improvement was evident: train and test performance had essentially
converged.
for our experiments because beyond that point, little
improvement was evident: train and test performance had essentially
converged.
Figure 5:
The
effect of varying the size of the training set on performance
for HUMRETBLAS.
 |
Our results so far have consisted of entropy estimates for sequences of
a single type. We now present the results of several cross-entropy
experiments. By this we mean that the type of the training set is different
from that of the test set. In table 3 mammalian coding regions and
non-coding regions form the two types. A substantial cross-entropic gap
is apparent. That is, a model trained on the coding sequence
might be used to distinguish coding from non-coding based on entropy. The same
is true when one trains on the non-coding sequence.
The same experiment produces very different results for yeast as shown in
table 4. While a large gap exists when one trains using
the non-coding regions, a reverse gap exists in the other case. That is,
training on the coding regions assigns shorter codes to the non-coding regions,
than to itself. While this effect is weak, it suggests that sequences from
the coding region may be echoed in the non-coding region.
Cross-species entropy estimates are interesting in general, but our
one example shown in table 5 shows little
interesting structure. That is, yeast coding regions teach nothing
about human coding regions and visa versa. In fact, the entropy
estimates are in both cases worse than random. In the non-coding
case, a weak relationship exists, but is easily explained by agreement
on the low order multigraphic statistics of the sequences, e.g.
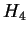 .
.
The entropy estimates we have discussed reduce to a single number the
model's performance on a sequence. It represents the average
code-length but says nothing about their distribution. The histograms
of figures 6,7, and
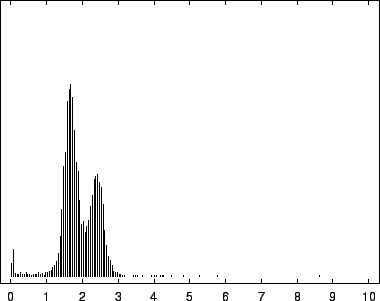
8, depict this distribution for the EBV
virus, the human gene HUMRETBLAS, and the yeast chromosome SCCHRIII. They present an interesting visual signature of a
sequence. Trimodality is apparent in all three, but is present to a
varying extent.
The first mode, most prevalent in our viral example, corresponds to
near-zero code-lengths that correspond to long exact or near-exact
repeats. In the viral case, this peak is particularly narrow because
while the sequence is known to contain several long exact repeats, it
lacks the full range of near repeats of various lengths found in
sequences such as HUMRETBLAS. The middle mode corresponds to
nucleotides having a long context that matches well with some other
segments from the sequence. In this case short codes are assigned so
long as these matches predict well the following nucleotide. The
rightmost mode, particularly pronounced in SCCHRIII and less so
in HUMRETBLAS, correspond to codes well over 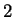 bits. Here the
model had a strong prediction, but was wrong.
bits. Here the
model had a strong prediction, but was wrong.
Figure 6:
Histogram of nucleotide code-lengths for EBV.
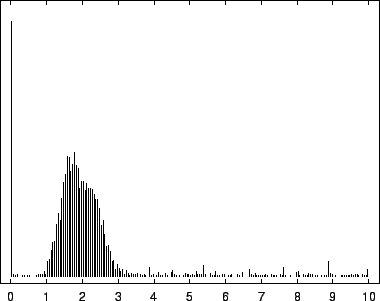 |
Figure 7:
Histogram of nucleotide code-lengths for HUMRETBLAS.
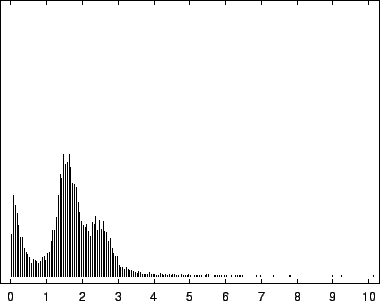 |
Figure 8:
Histogram of nucleotide code-lengths for SCCHRIII (yeast).
 |
The distribution of code-lengths displayed in these histograms says
nothing about how code-lengths are distributed with respect to
position in the DNA sequence. To visualize this we have plotted in
figures 9 and 10 the
code-lengths at  random positions for HUMRETBLAS and SCCHRIII. It is apparent that the distribution is not homogeneous
and presents another interesting visual signature of the sequence.
The distribution for HUMRETBLAS is shown at a
a closer scale (figure 11) where finer structure
is revealed.
The modality noted in the histograms is also apparent
in these plots.
random positions for HUMRETBLAS and SCCHRIII. It is apparent that the distribution is not homogeneous
and presents another interesting visual signature of the sequence.
The distribution for HUMRETBLAS is shown at a
a closer scale (figure 11) where finer structure
is revealed.
The modality noted in the histograms is also apparent
in these plots.
Figure 9:
The
variation of code-length with position for HUMRETBLAS.
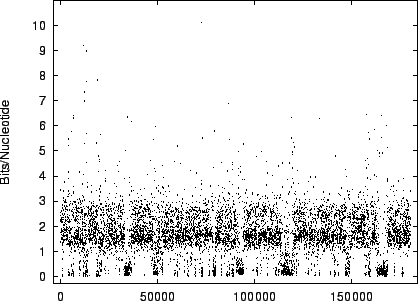 |
Figure 10:
The
variation of code-length with position for SCCHRIII
(yeast).
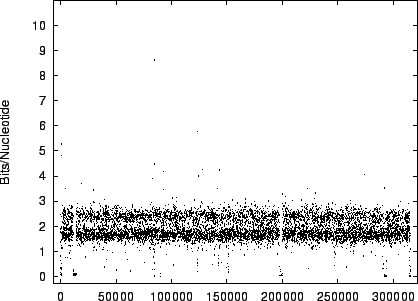 |
Figure 11:
The
variation of code-length with position for HUMRETBLAS in
the first 6,000 positions.
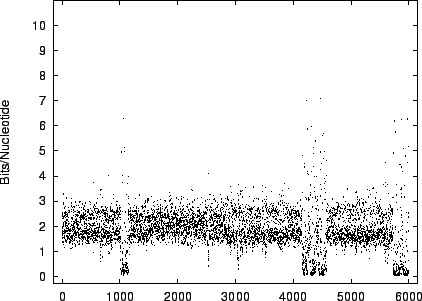 |
Alternative Metrics
Our model exploits near matches to form a prediction, and its
performance therefore depends on precisely what is meant by
near, i.e., the distance metric used to judge string
similarity. In this section we begin by discussing four
metrics and report on their performance.
The simplest notion of string distance relevant to our domain
is simple Hamming distance: the number of mismatching
nucleotides in two strings of equal length. We will refer to
this as the nucleotide-sense metric. As mentioned
earlier, our domain knowledge suggests that we also compare
the strings after reversing one, and complementing its bases.
Both distances are computed and the smaller one used. This is our
nucleotide-both metric, and was used in all experiments
from earlier sections.
Coding regions have additional structure which we capture in
another pair of metrics: amino-sense and
amino-both.
A common misconception is that coding regions should compress well
because three nucleotides together (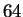 possibilities) code for only
one of
possibilities) code for only
one of 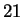 amino acids. This reasoning is flawed because
amino acids. This reasoning is flawed because 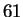 of the
of the
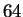 possibilities represent valid codes for amino acids. Only
possibilities represent valid codes for amino acids. Only 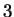 codes are used to stop transcription. Thus the maximum entropy
level for coding regions, is not
codes are used to stop transcription. Thus the maximum entropy
level for coding regions, is not
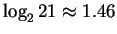 bits, nor
bits, nor
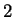 bits as for random unconstrained sequences, but rather is
bits as for random unconstrained sequences, but rather is
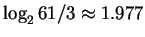 bits. In fact, it has been observed by several
authors that coding regions are less compressible than non-coding
regions
(e.g., [Mantegna et al., 1993,Salamon and Konopka, 1992,Farach et al., 1995]).
So it is clear that two sequences that code for
the same polypeptide may nevertheless have large Hamming
distance. The amino-sense distance between two strings whose
length is a multiple of 3, and that are assumed to be
aligned with the reading frame, is straightforward: it is
simply the number of mismatches in the amino acid sequence
coded by the nucleotide sequence; where the stop signal is
considered to be a 21st amino acid.
bits. In fact, it has been observed by several
authors that coding regions are less compressible than non-coding
regions
(e.g., [Mantegna et al., 1993,Salamon and Konopka, 1992,Farach et al., 1995]).
So it is clear that two sequences that code for
the same polypeptide may nevertheless have large Hamming
distance. The amino-sense distance between two strings whose
length is a multiple of 3, and that are assumed to be
aligned with the reading frame, is straightforward: it is
simply the number of mismatches in the amino acid sequence
coded by the nucleotide sequence; where the stop signal is
considered to be a 21st amino acid.
We extend this definition to the case in which the strings
being compared are not necessarily a multiple of 3 in length,
and we drop the assumption that they are aligned with the
reading frame. The comparison does however assume that the
strings are similarly aligned. If the first string
begins one base into the reading frame, it is assumed that the
other string does as well. That is, the strings must be in phase.
This assumption is appropriate because our search for near matches
will consider all possible positions, and in so doing all relative phases.
Selected experiments comparing these four metrics are shown in
table 66. Entire sequences as
well as their noncoding and coding regions were considered.
The nucleotide-both metric performs best, and was therefore
used for the experiments reported in earlier sections.
The amino metrics never outperformed their nucleotide
counterparts. This is not so surprising for entire sequences,
or noncoding regions, but we expected the amino metrics might
perform better for coding regions. In fact their estimates
are somewhat worse. Their poor performance is
explained by the fact that they distinguish fewer discrete
distances, and are always blind to the exact nucleotide
structure of the sequence, even in the positions immediately
before the base to be predicted.
The motivation in designing these metrics was the possibility
that coding regions might contain long nearly identical amino
acid sequences, which despite their nearness when expressed as
an amino acid sequence, are far apart when coded as
nucleotides. As explained above, our first attempt to capture
this domain knowledge in the model was unsuccessful, so we
tried another approach that produced a slightly stronger model for
coding regions.
Our second approach separates the prediction problem into two
stages. An amino acid is first predicted using CDNA based on
inexact matches, where the sequence is viewed at the amino
acid level, i.e., has alphabet size 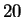 . Unlike our earlier
models, which make no assumption as to the nature of the DNA,
this model assumes that its input is a sequence of legal
codons. The model's second stage predicts
a particular codon, conditioned on the already predicted amino acid,
and on earlier positions which are now viewed at the nucleotide level.
The codon entropy estimate is then the sum of the entropies of these
two stages, and we write:
. Unlike our earlier
models, which make no assumption as to the nature of the DNA,
this model assumes that its input is a sequence of legal
codons. The model's second stage predicts
a particular codon, conditioned on the already predicted amino acid,
and on earlier positions which are now viewed at the nucleotide level.
The codon entropy estimate is then the sum of the entropies of these
two stages, and we write:
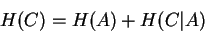 |
(10) |
Dividing 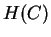 by three then gives a per-nucleotide entropy
which may be compared with earlier results. Table 7
gives the results of several models on our non-redundant data set.
by three then gives a per-nucleotide entropy
which may be compared with earlier results. Table 7
gives the results of several models on our non-redundant data set.
The first line of table 7 provides for
reference, the entropy corresponding to a uniformly random
sequence of codons. The next line reports the standard
multigraphic entropy 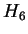 where alphabet is nucleotides
(
where alphabet is nucleotides
(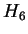 was optimal). Line three reports the result of the
CDNA program operating on a sequence of
nucleotides7. Its performance is
a mere
was optimal). Line three reports the result of the
CDNA program operating on a sequence of
nucleotides7. Its performance is
a mere 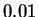 bits better than
bits better than  . The fourth line
reports the results from a two-stage model where the first
stage predicts an amino acid using a simple 2-gram model
(i.e., frequencies of amino acid pairs). The second stage
predicts a codon, based on the predicted amino acid, and the
two preceding nucleotides. In line 5, the 2-gram model is
replaced with CDNA program where the alphabet is now
amino acids, and windows from
. The fourth line
reports the results from a two-stage model where the first
stage predicts an amino acid using a simple 2-gram model
(i.e., frequencies of amino acid pairs). The second stage
predicts a codon, based on the predicted amino acid, and the
two preceding nucleotides. In line 5, the 2-gram model is
replaced with CDNA program where the alphabet is now
amino acids, and windows from 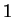 to
to 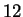 amino acids are
used. As for earlier experiments, the result on line five
arises from 8-way cross validation. Therefore, nearby matches
will not frequently contribute to a prediction. Line six
employs what amounts to maximal cross validation, where
a sequence element is predicted using everything else in the
sequence. The same technique was used to produce figures
9-11.
amino acids are
used. As for earlier experiments, the result on line five
arises from 8-way cross validation. Therefore, nearby matches
will not frequently contribute to a prediction. Line six
employs what amounts to maximal cross validation, where
a sequence element is predicted using everything else in the
sequence. The same technique was used to produce figures
9-11.
It is apparent that our non-redundant collection of coding
material is harder to model than the entire genes considered
in earlier sections. Nevertheless we are able to improve the
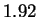 multigraphic estimate somewhat to
multigraphic estimate somewhat to 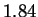 . It is
important to note our non-redundant data set is not a random
sample, but rather is closer to the worst case. We
expect that lower entropy estimates would result from random
samples of similar size, and remark that this was the case when
we considered Mammals/Coding-only in table 2.
There we reported an estimate of
. It is
important to note our non-redundant data set is not a random
sample, but rather is closer to the worst case. We
expect that lower entropy estimates would result from random
samples of similar size, and remark that this was the case when
we considered Mammals/Coding-only in table 2.
There we reported an estimate of 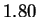 bits using CDNA at the
nucleotide level.
bits using CDNA at the
nucleotide level.
It is possible that the addition of more domain knowledge will
produce lower entropy estimates for coding regions. However,
we believe that the actual entropy may be not so far below our
current estimates. This is consistent with the view that the
coding regions of DNA commonly amount to a highly random
string, with only isolated critical regions.
If much of large proteins amounts to
scaffolding, and the bulk of proteins in a genome are
large, then we would expect large entropies. By scaffolding we mean
weakly constrained structure necessary only to ensure that
the protein folds correctly, and that particular active regions
are positioned properly in the resulting molecule.
There are certainly many genes that code for somewhat small proteins, but since
entropy is a per-base expected value, the genes that code for large
proteins have proportionaly greater affect on our estimate.
Figure 12 shows that in our non-redundant collection of
human genes, fewer than one third of bases are contained in coding regions
of length 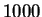 or less.
or less.
We conclude with a crude analysis to
quantify our belief. If only the hydrophobic/hydrophilic nature of
an amino acid were critical, then at most one bit would be required to
make an acceptable selection. This is then 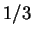 bit per base.
If, except for this structure, the string is random, then the lowest
entropy we would expect is:
bit per base.
If, except for this structure, the string is random, then the lowest
entropy we would expect is:
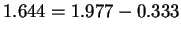 bits per base.
Biological experiments to quantify the sensitivity of proteins of
various length to mutation, would then shed light on the actual entropy of
coding regions.
bits per base.
Biological experiments to quantify the sensitivity of proteins of
various length to mutation, would then shed light on the actual entropy of
coding regions.
Figure 12:
The cumulative distribution of bases within the non-redundant
human gene set, as a function of the coding region length in which they appear
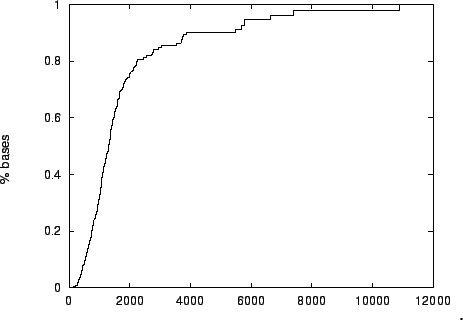 |
We have shown that the near repeats in natural DNA sequences
may be incorporated into a statistical model resulting in significantly
lower entropy estimates. For some sequences our model is the first
to detect substantial deviations from random behavior and illustrates
the importance of inexact string matching techniques in this field.
It is entirely possible that very different results will be obtained,
particularly for coding regions, when much more DNA is available for
analysis.
It should be noted that  entropy estimates include the known
effect of
entropy estimates include the known
effect of 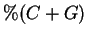 [Gatlin, 1972] on entropy estimation, and BIOCOMPRESS-2
includes the also known effect of long exact repeats and exact complement
repeats [Herzel et al., 1994].
CDNA's generally superior performance indicates that
DNA possesses more structure which may be exploited.
[Gatlin, 1972] on entropy estimation, and BIOCOMPRESS-2
includes the also known effect of long exact repeats and exact complement
repeats [Herzel et al., 1994].
CDNA's generally superior performance indicates that
DNA possesses more structure which may be exploited.
Several notions of distance were evaluated and the best
performance resulted from considering both Hamming distance to
reversed and complemented targets, as well as standard Hamming
distance, then selecting the minimum. We also described
two-stage models crafted especially for coding regions, which
perform better than our basic model on coding sequences.
Because of the observations in Section 2, a data compressor may be used as a
classifier, and the result interpreted in probabilistic terms. We
mention this because classification is one of the applications
motivating our work. To illustrate, suppose one has two long
sequences 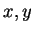 of DNA, the first of some type
of DNA, the first of some type 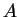 and the other of
type
and the other of
type 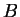 . The task is to classify a third strand
. The task is to classify a third strand 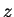 . Let
. Let 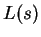 denote the bits output by the compressor when fed sequence
denote the bits output by the compressor when fed sequence 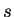 , and
, and
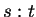 denote string concatenation. Then
denote string concatenation. Then 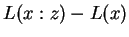 may by our
remarks above be interpreted as
may by our
remarks above be interpreted as
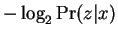 . Similarly
. Similarly
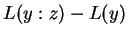 corresponds to
corresponds to
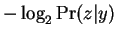 . At this point one
might simply compare to affect classification, or exponentiate
yielding probabilities. These can then be combined along with prior
class probabilities, resulting in Bayesian classifier built from data
compressors.
. At this point one
might simply compare to affect classification, or exponentiate
yielding probabilities. These can then be combined along with prior
class probabilities, resulting in Bayesian classifier built from data
compressors.
Future work will consider stronger models exploiting
additional effects. The current assumption that each
prediction event is independent of the last may be dropped and
a temporal dependence component added to the model. Next the
metric may be enhanced to notice not only the number of
mismatches, but also where they occur. Other structural
changes are possible and the inclusion of additional domain
knowledge in some form is a particularly interesting
direction. Also, there are entirely different approaches one
might take to the problem of combining experts.
Because of our interest in alternative metrics, simple linear search
is used to find near matches. Our results indicate that
standard Hamming distance performs well, so we plan to implement more
advanced sublinear algorithms for this purpose.
Finally, we plan to investigate the application of these new,
stronger models to various applications in the microbiological
field.
We thank Martin Farach, Haym Hirsh, Harold Stone, and Sarah Zelikovitz
for helpful comments on earlier drafts of this paper. We also thank
Michiel Noordewier for the use of the large, non-redundant human gene
set.
- Baum, 1972
-
Baum, L. E. (1972).
An inequality and associated maximization technique in statistical
estimatation of probabilistic functions of Markov processes.
Inequalities, 3:1-8.
- Baum and Eagon, 1967
-
Baum, L. E. and Eagon, J. E. (1967).
An inequality with application to statistical estimation for
probabalistic functions of a Markov process and to models for ecology.
Bull. AMS, 73:360-363.
- Baum et al., 1970
-
Baum, L. E., Petrie, T., Soules, G., and Weiss, N. (1970).
A maximization technique occurring in the statistical analysis of
probabilistic functions of Markov chains.
Ann. Math Stat., 41:164-171.
- Bell et al., 1990
-
Bell, T. C., Cleary, J. G., and Witten, I. H. (1990).
Text Compression.
Prentice Hall.
- Cardon and Stormo, 1992
-
Cardon, L. and Stormo, G. (1992).
Expectation maximization algorithm for identifying protein-binding
sites with variable lengths from unaligned DNA fragments.
JMB, 223:159-170.
- Cosmi et al., 1990
-
Cosmi, C., Cuomo, V., Ragosta, M., and Macchiato, M. (1990).
Characterization of nucleotidic sequences using maximum entropy
techniques.
J. Theor. Biol, (147):423-432.
- Cover and Thomas, 1991
-
Cover, T. M. and Thomas, J. A. (1991).
Elements of Information Theory.
Wiley.
- Dempster et al., 1977
-
Dempster, A. P., Laird, N. M., and Rubin, D. B. (1977).
Maximum-likelihood from incomplete data via the EM algorithm.
J. Royal Statistical Society Ser. B (methodological), 39:1-38.
- Dujon et al., 1994
-
Dujon, B., Alexandraki, D., Andre, B., Ansorge, W., and et al., V. B. (1994).
Complete DNA sequence of yeast chromosome XI.
Nature, 369:371-378.
- Farach et al., 1995
-
Farach, M., Noordewier, M., Savari, S., Shepp, L., Wyner, A., and Ziv, J.
(1995).
On the entropy of DNA: Algorithms and measurements based on memory
and rapid convergence.
In Proceedings of the Sixth Annual ACM-SIAM Symposium on
Discrete Algorithms, pages 48-57, San Francisco. SIAM/ACM-SIGACT.
- Gatlin, 1972
-
Gatlin, L. L. (1972).
Information Theory and the Living System.
Columbia University Press, New York.
- Grumbach and Tahi, 1994
-
Grumbach, S. and Tahi, F. (1994).
A new challenge for compression algorithms: genetic sequences.
Information Processing & Management, 30(6):875-886.
- Herzel, 1988
-
Herzel, H. (1988).
Complexity of symbol sequences.
Syst. Anal. Modl. Simul., 5(5):435-444.
- Herzel et al., 1994
-
Herzel, H., Ebeling, W., and Schmitt, A. (1994).
Entropies of biosequences: The role of repeats.
Physical Review E, 50(6):5061-5071.
- Krogh et al., 1994
-
Krogh, A., Mian, I., and Haussler, D. (1994).
A hidden Markov model that finds genes in Escheria Coli DNA.
Nucleic Acids Research supplement, 22:4768-4778.
- Lauc et al., 1992
-
Lauc, G., Ilic, I., and Heffer-Lauc, H. (1992).
Entropies of coding and noncoding sequences of DNA and proteins.
Biophysical Chemistry, (42):7-11.
- Mantegna et al., 1993
-
Mantegna, R., Buldyrev, S., Goldberger, A., Havlin, S., Peng, C.-K., Simons,
M., and Stanley, H. (1993).
Linguistic features of noncoding DNA sequences.
Physical Review Letters, 73(23):3169-3172.
- Noordewier, 1996
-
Noordewier, M. (1996).
Private Communication. Available at
http://paul.rutgers.edu/~loewenst/cdna.html.
- Poritz, 1988
-
Poritz, A. B. (1988).
Hidden Markov models: a guided tour.
In Proc. ICASSP-88, volume 1, pages 7-13, New York. IEEE.
- Redner and Walker, 1984
-
Redner, R. A. and Walker, H. F. (1984).
Mixture densities, maximum likelihood, and the EM algorithm.
SIAM Review, 26:195-239.
- Salamon and Konopka, 1992
-
Salamon, P. and Konopka, A. K. (1992).
A maximum entropy principle for the distribution of local complexity
in naturally occurring nucleotide sequences.
Computers Chem., 16(2):117-124.
- Yianilos, 1997
-
Yianilos, P. N. (1997).
Topics in Computational Hidden State Modeling.
PhD thesis, Dept. of Computer Science, Princeton University.
- Ziv and Lempel, 1977
-
Ziv, J. and Lempel, A. (1977).
A universal algorithm for sequential data compression.
IEEE Transactions on Information Theory, IT-23(3).
Table:
Predicted vs. observed matches (HUMRETBLAS,
window size 20). Contexts of length 20 from the first 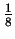 were matched to contexts in the subsequent
were matched to contexts in the subsequent 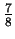 of the gene.
of the gene.
| Hamming |
Expected |
Observed |
. | % hit at |
. | % correct |
|
| Distance |
# Matches |
# Matches |
. | least once |
. | given 1+ hits |
|
| 0 |
1 |
. | 44
 |
0 |
. | 387 |
4 |
. | 4% |
90.91% |
| 1 |
8 |
. | 61
 |
0 |
. | 143 |
7 |
. | 2 |
83.77 |
| 2 |
2 |
. | 45
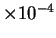 |
0 |
. | 278 |
11 |
. | 0 |
78.19 |
| 3 |
4 |
. | 42
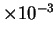 |
0 |
. | 505 |
17 |
. | 6 |
66.00 |
| 4 |
0 |
. | 0563 |
1 |
. | 184 |
33 |
. | 2 |
45.91 |
| 5 |
0 |
. | 541 |
4 |
. | 148 |
78 |
. | 2 |
35.86 |
| 6 |
4 |
. | 01 |
18 |
. | 759 |
98 |
. | 3 |
31.90 |
| 7 |
24 |
. | 3 |
80 |
. | 69 |
100 |
. | |
29.19 |
| 8 |
119 |
. | |
304 |
. | 9 |
100 |
. | |
28.35 |
| 9 |
475 |
. | |
986 |
. | 0 |
100 |
. | |
28.09 |
| 10 |
1566 |
. | |
2713 |
. | |
100 |
. | |
27.86 |
| 11 |
4271 |
. | |
6286 |
. | |
100 |
. | |
27.68 |
| 12 |
9609 |
. | |
12300 |
. | |
100 |
. | |
27.53 |
| 13 |
17740 |
. | |
20172 |
. | |
100 |
. | |
27.33 |
| 14 |
26610 |
. | |
27387 |
. | |
100 |
. | |
27.09 |
| 15 |
31932 |
. | |
30356 |
. | |
100 |
. | |
26.86 |
| 16 |
29936 |
. | |
26813 |
. | |
100 |
. | |
26.57 |
| 17 |
21131 |
. | |
18200 |
. | |
100 |
. | |
26.28 |
| 18 |
10566 |
. | |
8931 |
. | |
100 |
. | |
25.94 |
| 19 |
3337 |
. | |
2826 |
. | |
100 |
. | |
25.69 |
| 20 |
500 |
. | |
434 |
. | 5 |
100 |
. | |
25.43 |
|
Table 2:
Summary of entropy estimates (bits/nucleotide).
| |
|
Algorithm |
| |
|
UNIX |
|
|
|
|
bio-com- |
CDNA |
| sequence |
length |
compress |
 |
 |
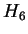 |
CDNA |
press-2 |
compress |
| Mammals |
|
|
|
|
|
|
|
|
| 14 Sequences |
1029151 |
2.19 |
1.98 |
1.91 |
1.91 |
1.67 |
|
|
| Coding only |
46457 |
2.19 |
1.99 |
1.94 |
1.94 |
1.80 |
|
|
| Noncoding only |
982694 |
2.11 |
1.98 |
1.92 |
1.90 |
1.74 |
|
|
| HUMDYSTROP |
38770 |
2.23 |
1.95 |
1.91 |
1.95 |
1.91 |
1.93 |
1.93 |
| HUMGHCSA |
66495 |
2.19 |
2.00 |
1.92 |
1.86 |
0.54 |
1.31 |
0.95 |
| HUMHBB |
73308 |
2.20 |
1.97 |
1.91 |
1.92 |
1.68 |
1.88 |
1.77 |
| HUMHDABCD |
58864 |
2.21 |
2.00 |
1.92 |
1.89 |
1.63 |
1.88 |
1.67 |
| HUMHPRTB |
56737 |
2.20 |
1.97 |
1.91 |
1.90 |
1.69 |
1.91 |
1.72 |
| HUMRETBLAS |
180388 |
2.14 |
1.95 |
1.90 |
1.90 |
1.66 |
|
1.75 |
| Yeast Chromosome III |
315338 |
2.18 |
1.96 |
1.94 |
1.95 |
1.90 |
1.92 |
1.94 |
| Coding only |
211551 |
2.20 |
1.97 |
1.95 |
1.96 |
1.92 |
|
|
| Noncoding only |
103787 |
2.19 |
1.93 |
1.91 |
1.92 |
1.85 |
|
|
| Mitochondria |
|
|
|
|
|
|
|
|
| MPOMTCG |
186609 |
2.20 |
1.98 |
1.96 |
1.96 |
1.83 |
1.94 |
1.87 |
| PANMTPACGA |
100314 |
2.12 |
1.88 |
1.86 |
1.86 |
1.81 |
1.88 |
1.85 |
| Other Eukaryotes |
|
|
|
|
|
|
|
|
| CEC07A9 |
66004 |
2.20 |
1.94 |
1.90 |
1.92 |
1.89 |
|
|
| CHNTXX |
155844 |
2.19 |
1.96 |
1.93 |
1.93 |
1.30 |
1.62 |
1.65 |
| Prokaryotes |
|
|
|
|
|
|
|
|
| 7 sequences |
784658 |
2.22 |
2.00 |
1.95 |
1.95 |
1.92 |
|
|
| Eukaryotic Viruses |
|
|
|
|
|
|
|
|
| 5 sequences |
650477 |
2.15 |
1.94 |
1.91 |
1.91 |
1.66 |
|
|
| EBV |
172281 |
2.17 |
1.97 |
1.93 |
1.91 |
1.54 |
|
|
| VACCG |
191737 |
2.14 |
1.92 |
1.90 |
1.90 |
1.69 |
1.76 |
1.81 |
| Bacteriophages |
|
|
|
|
|
|
|
|
| 3 sequences |
140739 |
2.25 |
1.98 |
1.94 |
1.94 |
1.93 |
|
|
|
Table 3:
Mammalian corpus cross-entropies (bits/nucleotide).
| Training |
Test
Data |
| Set |
Coding |
Noncoding |
| Coding |
1.829 |
2.010 |
| Noncoding |
1.949 |
1.727 |
|
Table 4:
Yeast chromosome III cross-entropies (bits/nucleotide).
| Training |
Test
Data |
| Set |
Coding |
Noncoding |
| Coding |
1.941 |
1.918 |
| Noncoding |
1.982 |
1.831 |
|
Table 5:
Yeast/Mammalian cross-entropies (bits/nucleotide).
| Training Set |
Test Set |
Entropy |
| Mammalian Coding |
Yeast Coding |
2.026 |
| Mammalian
Noncoding |
Yeast Noncoding |
1.927 |
| Yeast Coding |
Mammalian
Coding |
2.033 |
| Yeast Noncoding |
Mammalian Noncoding |
1.955 |
|
Table 6:
Effect of metric on entropy estimate (bits/nucleotide).
| |
nucleotide |
amino acid |
| sequence |
sense |
both |
sense |
both |
| Mammals |
|
|
|
|
| Coding only |
1.830 |
1.830 |
1.882 |
1.895 |
| Noncoding only |
1.750 |
1.727 |
1.795 |
1.769 |
| HUMGHCSA |
0.525 |
0.510 |
0.550 |
0.547 |
| HUMRETBLAS |
1.748 |
1.686 |
1.799 |
1.731 |
| SCCHRIII |
1.904 |
1.879 |
1.930 |
1.926 |
| Coding only |
1.947 |
1.941 |
1.966 |
1.970 |
| Noncoding only |
1.879 |
1.831 |
1.889 |
1.850 |
| Prokaryotes |
|
|
|
|
| 7 sequences |
1.944 |
1.939 |
1.977 |
1.977 |
|
Table:
Summary of modeling results
(bits/nucleotide) for coding regions extracted from a
non-redundant collection of 490 human genes .
| |
Model Description |
bits |
| 1. |
Max. Entropy |
1.98 |
| 2. |
Nucleotide 6-grams |
1.92 |
| 3. |
CDNA nucleotide |
1.91 |
| 4. |
Amino 2-grams + Codon-predict |
1.89 |
| 5. |
CDNA amino (8 way) + Codon-predict |
1.87 |
| 6. |
CDNA amino (max. way) + Codon-predict |
1.84 |
|
Significantly Lower Entropy Estimates for Natural DNA Sequences
This document was generated using the
LaTeX2HTML translator Version 2K.1beta (1.47)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -image_type gif -nonext_page_in_navigation -noprevious_page_in_navigation -up_url ../main.html -up_title 'Publication homepage' -numbered_footnotes cdna.tex
The translation was initiated by Peter N. Yianilos on 2002-06-30
Footnotes
- ... bits.1
- This gap may be thought of as
the mutual information between the nucleotide being predicted,
and its past.
- ...
character2
- As implemented in the UNIX (registered
trademark of X/Open Company, Ltd.) compress utility.
- ...
well-behaved3
- It is sufficient for example that the process be
stationary and ergodic -- see the Shannon-McMillan-Breiman theorem.
- ... symbol4
- Unfortunately this isn't exactly correct for all data
compression schemes, e.g. for Lempel-Ziv coding. The heart of
the problem is that these codes consider only the greedy parse of the
sequence. By this we mean that if one sums over all sequences of
length
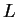 their inferred probability
their inferred probability
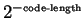 , one
will not obtain unity. In most cases the sum is strictly less than
unity and the inferred probabilities may be thought of as proportional
to probabilities. The result is that entropy estimates are increased
by a positive additive constant. In practice however, the discrepancy
is modest and one may without harm think of codes as corresponding to
probabilities.
, one
will not obtain unity. In most cases the sum is strictly less than
unity and the inferred probabilities may be thought of as proportional
to probabilities. The result is that entropy estimates are increased
by a positive additive constant. In practice however, the discrepancy
is modest and one may without harm think of codes as corresponding to
probabilities.
- ... optima.5
- We noted the entropy
estimates of HUMRETBLAS using different randomly generated
initial probability distributions. As the number of EM iterations
increases, each distribution converges to a different (though similar)
value (cf. Figure 3).
- ...table:metric6
- These data were collected
using smaller numbers of training and test samples than those
presented in table 2.
- ... nucleotides7
- Same parameters as for earlier
experiments, but 2,000 training samples
Up: Publication homepage
Peter N. Yianilos
2002-06-30
![]() ,
an optimal code would assign
,
an optimal code would assign ![]() bits to each nucleotide. DNA
may be imagined to be a highly ordered, purposeful molecule, and
one might therefore reasonably expect statistical models of its
string representation to produce much lower entropy estimates.
Surprisingly this has not been the case for many natural DNA
sequences, including portions of the human genome. We
introduce a new statistical model (compression algorithm), the
strongest reported to date, for naturally occurring DNA
sequences. Conventional techniques code a nucleotide using
only slightly fewer bits (1.90) than one obtains by relying only on
the frequency statistics of individual nucleotides (1.95). Our
method in some cases increases this gap by more than
five-fold (1.66) and may lead to better performance in
microbiological pattern recognition applications.
bits to each nucleotide. DNA
may be imagined to be a highly ordered, purposeful molecule, and
one might therefore reasonably expect statistical models of its
string representation to produce much lower entropy estimates.
Surprisingly this has not been the case for many natural DNA
sequences, including portions of the human genome. We
introduce a new statistical model (compression algorithm), the
strongest reported to date, for naturally occurring DNA
sequences. Conventional techniques code a nucleotide using
only slightly fewer bits (1.90) than one obtains by relying only on
the frequency statistics of individual nucleotides (1.95). Our
method in some cases increases this gap by more than
five-fold (1.66) and may lead to better performance in
microbiological pattern recognition applications.